苏科版七年级数学上册试题 4.3用一元一次方程解决问题--几何问题-(含答案)
文档属性
| 名称 | 苏科版七年级数学上册试题 4.3用一元一次方程解决问题--几何问题-(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 133.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 19:56:07 | ||
图片预览


文档简介
4.3用一元一次方程解决问题--几何问题
一、选择题.
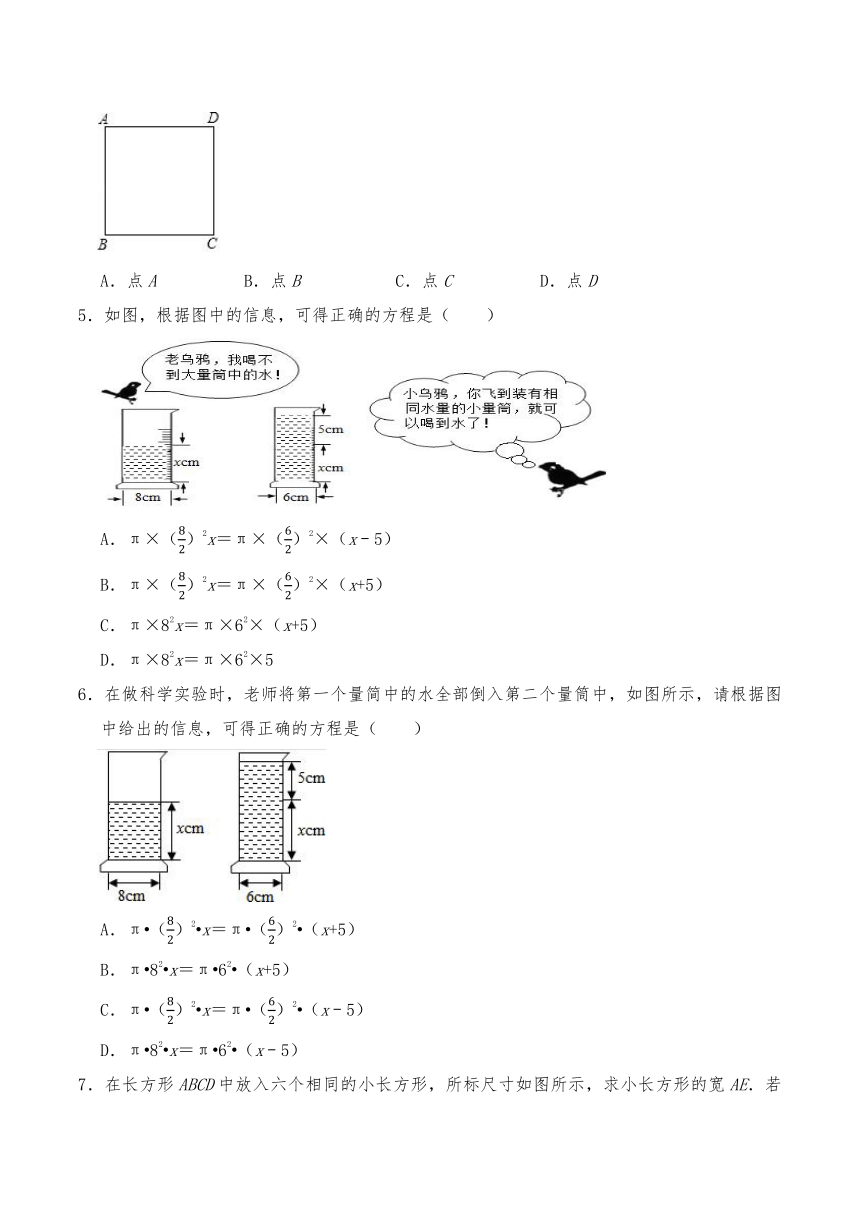
1.如图所示,两人沿着边长为90m的正方形,按A→B→C→D→A…的方向行走,甲从A点以65m/min的速度、乙从B点以75m/min的速度行走,当乙第一次追上甲时,将在正方形的( )边上.
A.BC B.DC C.AD D.AB
2.如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.
A.400 B.500 C.300 D.750
3.正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1cm,乙的速度为每秒5cm,已知正方形轨道ABCD的边长为2cm,则乙在第2019次追上甲时的位置( )
A.AB上 B.BC上 C.CD上 D.AD上
4.如图,电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动,电子蚂蚁P从点A出发,以个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以个单位长度/秒的速度绕正方形作逆时针运动,则它们第2018次相遇在( )
A.点A B.点B C.点C D.点D
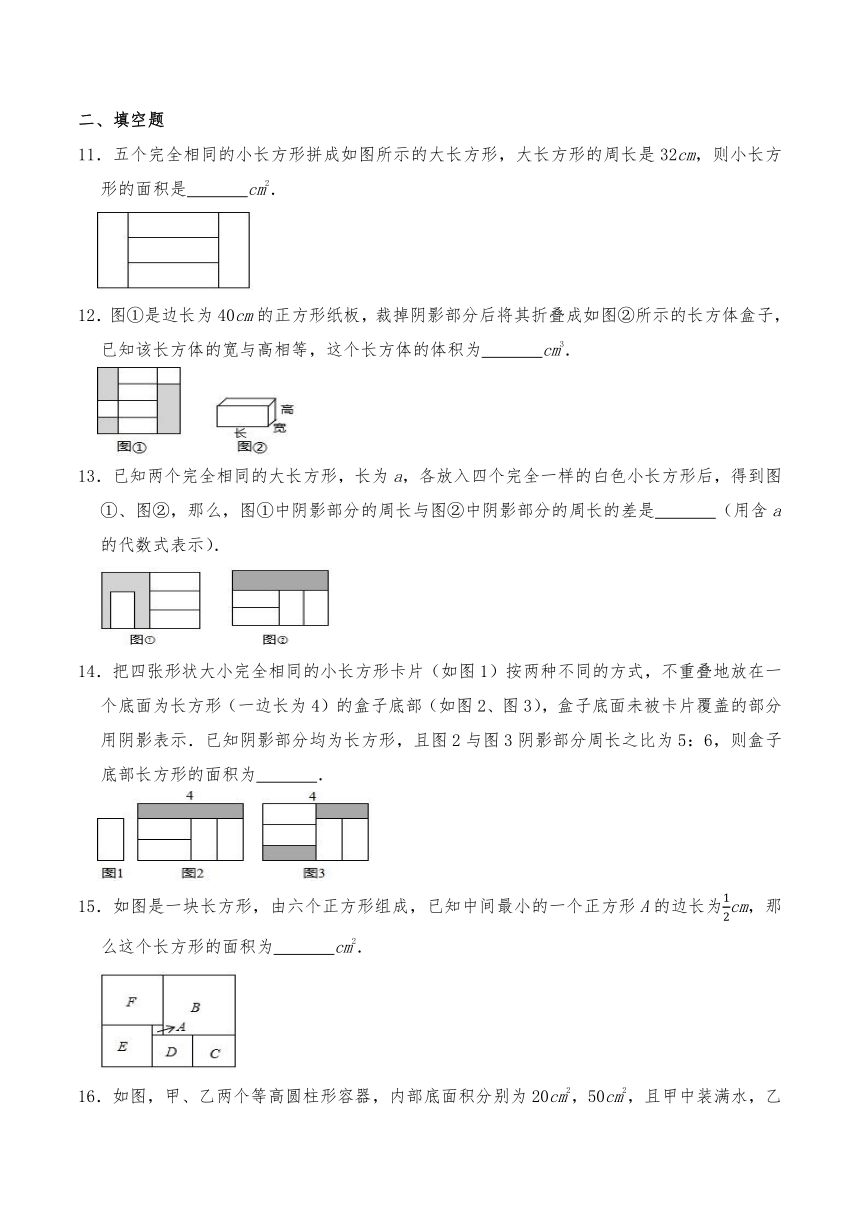
5.如图,根据图中的信息,可得正确的方程是( )
A.π×()2x=π×()2×(x﹣5)
B.π×()2x=π×()2×(x+5)
C.π×82x=π×62×(x+5)
D.π×82x=π×62×5
6.在做科学实验时,老师将第一个量简中的水全部倒入第二个量筒中,如图所示,请根据图中给出的信息,可得正确的方程是( )
A.π ()2 x=π ()2 (x+5)
B.π 82 x=π 62 (x+5)
C.π ()2 x=π ()2 (x﹣5)
D.π 82 x=π 62 (x﹣5)
7.在长方形ABCD中放入六个相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若设AE=x(cm),依题意可得方程( )
A.16﹣3x=8 B.8+2x=16﹣3x
C.8+2x=16﹣x D.8+2x=x+(16﹣3x)
8.如图,正方形ABCD的边长是2个单位,一只乌龟从A点出发以2个单位/秒的速度顺时针绕正方形运动,另有一只兔子也从A点出发以6个单位/秒的速度逆时针绕正方形运动,则第2020次相遇在( )
A.点A B.点B C.点C D.点D
9.如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条,如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和为( )
A.215cm2 B.250cm2 C.300cm2 D.320cm2
10.在长方形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若设AE=x(cm),则由题意,得方程( )
A.14﹣3x=6 B.14﹣3x=6+2x
C.6+2x=x+(14﹣3x) D.6+2x=14﹣x
二、填空题
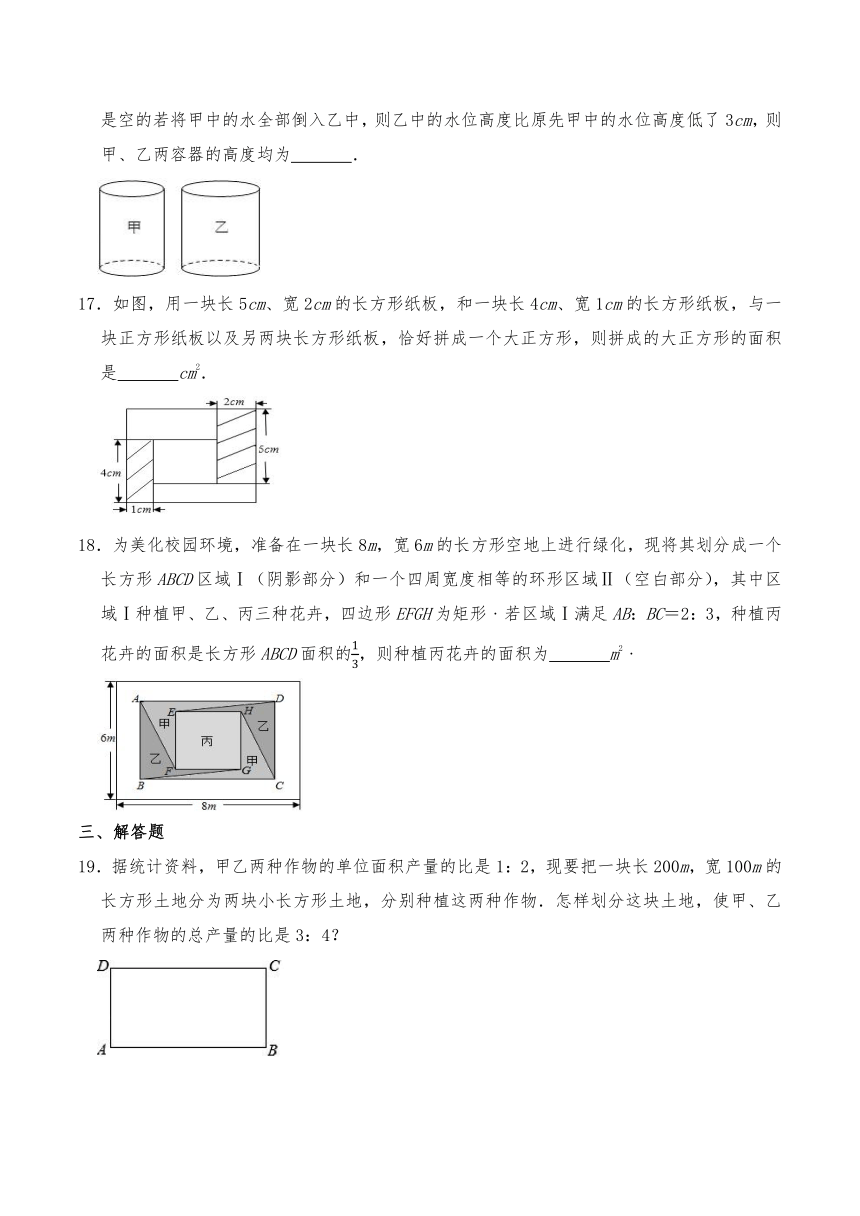
11.五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是 cm2.
12.图①是边长为40cm的正方形纸板,裁掉阴影部分后将其折叠成如图②所示的长方体盒子,已知该长方体的宽与高相等,这个长方体的体积为 cm3.
13.已知两个完全相同的大长方形,长为a,各放入四个完全一样的白色小长方形后,得到图①、图②,那么,图①中阴影部分的周长与图②中阴影部分的周长的差是 (用含a的代数式表示).
14.把四张形状大小完全相同的小长方形卡片(如图1)按两种不同的方式,不重叠地放在一个底面为长方形(一边长为4)的盒子底部(如图2、图3),盒子底面未被卡片覆盖的部分用阴影表示.已知阴影部分均为长方形,且图2与图3阴影部分周长之比为5:6,则盒子底部长方形的面积为 .
15.如图是一块长方形,由六个正方形组成,已知中间最小的一个正方形A的边长为cm,那么这个长方形的面积为 cm2.
16.如图,甲、乙两个等高圆柱形容器,内部底面积分别为20cm2,50cm2,且甲中装满水,乙是空的若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲中的水位高度低了3cm,则甲、乙两容器的高度均为 .
17.如图,用一块长5cm、宽2cm的长方形纸板,和一块长4cm、宽1cm的长方形纸板,与一块正方形纸板以及另两块长方形纸板,恰好拼成一个大正方形,则拼成的大正方形的面积是 cm2.
18.为美化校园环境,准备在一块长8m,宽6m的长方形空地上进行绿化,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个四周宽度相等的环形区域Ⅱ(空白部分),其中区域Ⅰ种植甲、乙、丙三种花卉,四边形EFGH为矩形﹒若区域Ⅰ满足AB:BC=2:3,种植丙花卉的面积是长方形ABCD面积的,则种植丙花卉的面积为 m2﹒
三、解答题
19.据统计资料,甲乙两种作物的单位面积产量的比是1:2,现要把一块长200m,宽100m的长方形土地分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
20.如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米,
(1)若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;
(2)观察图形的特点可知,长方形相对的两边是相等的(如图中的MN和PQ).请根据这个等量关系,求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?
21.某中学校为给学生营造良好舒适的休息环境,决定改造校园内的一小花园,如图是该花园的平面示意图,它是由6个正方形拼成的长方形用以种植六种不同的植物,已知中间最小的正方形A的边长是2米,正方形C、D边长相等.请根据图形特点求出该花园的总面积.
22.如图,长方形ABCD中,AB=4cm,BC=8cm.点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→D→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了3cm,并沿B→C→D→A的路径匀速运动;点Q保持速度不变,继续沿原路径匀速运动,某一时刻两点在长方形ABCD某一边上的E点处第二次相遇.若点Q的速度为cm/s.
(1)点P原来的速度为 cm/s;
(2)P、Q两点在B点处首次相遇后,再经过 秒后第二次在E点相遇;
(3)E点在 边上.此时S△DCE= cm2;
(4)在E点相遇后P、Q两点沿原来的方向继续前进.又经历了99次相遇后停止运动,请问此时两点停在长方形ABCD边上的什么位置?
23.小明用8个完全相同的小长方形拼图,拼出了如图甲、乙的两种图案:图案甲是一个正方形,图案乙是一个大的长方形;图案甲的中间留下了边长是1的正方形小洞.
(1)设每个小方形的宽为x,由图乙可知每个小长方形的长可表示为 .
(2)求小长方形的长和宽.
24.如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条.如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和.
答案
一、选择题.
C.A.C.C.B.A.D.A.C.C.
二、填空题
11.12
12.2000
13.a.
14.12.
15.
16.5cm.
17.36.
18.8.
三、解答题
19.解:∵甲、乙两种作物的单位面积产量的比是1:2,
∴要使甲、乙两种作物的总产量的比是 3:4,
则设种植甲作物的面积为:x,种植乙作物的面积为:(20000﹣x),
∴:1:2,
解得:x=12000,
∴种植乙作物的面积为:20000﹣12000=8000,
分法:
甲的种植长度为120,宽度100,或者长度为200,宽度为60;
乙的种植长度100,宽度80或者长度200,宽度为40
即可得出符合要求的两部分.
20.解:(1)若设图中最大正方形B的边长是x米,最小的正方形的边长是1米.
F的边长为(x﹣1)米,
C的边长为,
E的边长为(x﹣1﹣1);
(2)∵MQ=PN,
∴x﹣1+x﹣2=x,
x=7,
x的值为7;
(3)设余下的工程由乙队单独施工,还要x天完成.
()×2x=1,
x=10(天).
答:余下的工程由乙队单独施工,还要10天完成.
21.解:设图中最大正方形B的边长是x米,
∵最小的正方形的边长是2米,
∴正方形F的边长为(x﹣2)米,正方形E的边长为(x﹣4)米,正方形C的边长为米.
∵MQ=PN,
∴x﹣2+x﹣4=x米,
解得:x=14.
则QM=12+10=22(米),PQ=12+14=26(米)
故该花园的总面积=22×26=572(平方米).
答:该花园的总面积是572平方米.
22.解:(1)设点P原来的速度为xcm/s,根据题意得,
,
解得,x,
经检验,x是原方程的解,
故答案为:;
(2)设P、Q两点在B点处首次相遇后,再经过y秒后第二次在E点相遇,根据题意得,
,
解得,y=3,
故答案为:3;
(3)由(2)知,B到E点的路程长度为:(cm),
∵10﹣AB=10﹣4=6<AD,
∴E点在AD边上,且AE=6(cm),
∴DE=AD﹣AE=8﹣6=2(cm),
∴(cm2),
故答案为:AD;4;
(4)由(3)知,当P、Q相遇一次,则Q行驶(cm),
由由此知得,如下图,E1、E2、E3…,依次为P、Q相遇第一次、第二次、第三次…的位置,
由上可知,P、Q两点每相遇12次,就与前面12个位置依次重复,
∵99÷12=8…3,
∴P、Q两点经历了99次相遇后停止的位置在E3处,
∴P、Q两点经历了99次相遇后停止,此时两点停在长方形ABCD边上的C点位置.
23.解:(1)由题意知,每个小长方形的长为:.
故答案是:.
(2)依题意,得.
解得x=3.
答:每个小长方形的长为5,宽为3.
24.解:设原来正方形纸的边长是xcm,则第一次剪下的长条的长是xcm,宽是5cm,第二次剪下的长条的长是(x﹣5)cm,宽是6cm,
则5x=6(x﹣5),
解得:x=30
30×5×2=300(cm2),
答:两个所剪下的长条的面积之和为300cm2.
一、选择题.
1.如图所示,两人沿着边长为90m的正方形,按A→B→C→D→A…的方向行走,甲从A点以65m/min的速度、乙从B点以75m/min的速度行走,当乙第一次追上甲时,将在正方形的( )边上.
A.BC B.DC C.AD D.AB
2.如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )cm2.
A.400 B.500 C.300 D.750
3.正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1cm,乙的速度为每秒5cm,已知正方形轨道ABCD的边长为2cm,则乙在第2019次追上甲时的位置( )
A.AB上 B.BC上 C.CD上 D.AD上
4.如图,电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动,电子蚂蚁P从点A出发,以个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以个单位长度/秒的速度绕正方形作逆时针运动,则它们第2018次相遇在( )
A.点A B.点B C.点C D.点D
5.如图,根据图中的信息,可得正确的方程是( )
A.π×()2x=π×()2×(x﹣5)
B.π×()2x=π×()2×(x+5)
C.π×82x=π×62×(x+5)
D.π×82x=π×62×5
6.在做科学实验时,老师将第一个量简中的水全部倒入第二个量筒中,如图所示,请根据图中给出的信息,可得正确的方程是( )
A.π ()2 x=π ()2 (x+5)
B.π 82 x=π 62 (x+5)
C.π ()2 x=π ()2 (x﹣5)
D.π 82 x=π 62 (x﹣5)
7.在长方形ABCD中放入六个相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若设AE=x(cm),依题意可得方程( )
A.16﹣3x=8 B.8+2x=16﹣3x
C.8+2x=16﹣x D.8+2x=x+(16﹣3x)
8.如图,正方形ABCD的边长是2个单位,一只乌龟从A点出发以2个单位/秒的速度顺时针绕正方形运动,另有一只兔子也从A点出发以6个单位/秒的速度逆时针绕正方形运动,则第2020次相遇在( )
A.点A B.点B C.点C D.点D
9.如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条,如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和为( )
A.215cm2 B.250cm2 C.300cm2 D.320cm2
10.在长方形ABCD中放入六个长、宽都相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若设AE=x(cm),则由题意,得方程( )
A.14﹣3x=6 B.14﹣3x=6+2x
C.6+2x=x+(14﹣3x) D.6+2x=14﹣x
二、填空题
11.五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是 cm2.
12.图①是边长为40cm的正方形纸板,裁掉阴影部分后将其折叠成如图②所示的长方体盒子,已知该长方体的宽与高相等,这个长方体的体积为 cm3.
13.已知两个完全相同的大长方形,长为a,各放入四个完全一样的白色小长方形后,得到图①、图②,那么,图①中阴影部分的周长与图②中阴影部分的周长的差是 (用含a的代数式表示).
14.把四张形状大小完全相同的小长方形卡片(如图1)按两种不同的方式,不重叠地放在一个底面为长方形(一边长为4)的盒子底部(如图2、图3),盒子底面未被卡片覆盖的部分用阴影表示.已知阴影部分均为长方形,且图2与图3阴影部分周长之比为5:6,则盒子底部长方形的面积为 .
15.如图是一块长方形,由六个正方形组成,已知中间最小的一个正方形A的边长为cm,那么这个长方形的面积为 cm2.
16.如图,甲、乙两个等高圆柱形容器,内部底面积分别为20cm2,50cm2,且甲中装满水,乙是空的若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲中的水位高度低了3cm,则甲、乙两容器的高度均为 .
17.如图,用一块长5cm、宽2cm的长方形纸板,和一块长4cm、宽1cm的长方形纸板,与一块正方形纸板以及另两块长方形纸板,恰好拼成一个大正方形,则拼成的大正方形的面积是 cm2.
18.为美化校园环境,准备在一块长8m,宽6m的长方形空地上进行绿化,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个四周宽度相等的环形区域Ⅱ(空白部分),其中区域Ⅰ种植甲、乙、丙三种花卉,四边形EFGH为矩形﹒若区域Ⅰ满足AB:BC=2:3,种植丙花卉的面积是长方形ABCD面积的,则种植丙花卉的面积为 m2﹒
三、解答题
19.据统计资料,甲乙两种作物的单位面积产量的比是1:2,现要把一块长200m,宽100m的长方形土地分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
20.如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米,
(1)若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;
(2)观察图形的特点可知,长方形相对的两边是相等的(如图中的MN和PQ).请根据这个等量关系,求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?
21.某中学校为给学生营造良好舒适的休息环境,决定改造校园内的一小花园,如图是该花园的平面示意图,它是由6个正方形拼成的长方形用以种植六种不同的植物,已知中间最小的正方形A的边长是2米,正方形C、D边长相等.请根据图形特点求出该花园的总面积.
22.如图,长方形ABCD中,AB=4cm,BC=8cm.点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→D→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了3cm,并沿B→C→D→A的路径匀速运动;点Q保持速度不变,继续沿原路径匀速运动,某一时刻两点在长方形ABCD某一边上的E点处第二次相遇.若点Q的速度为cm/s.
(1)点P原来的速度为 cm/s;
(2)P、Q两点在B点处首次相遇后,再经过 秒后第二次在E点相遇;
(3)E点在 边上.此时S△DCE= cm2;
(4)在E点相遇后P、Q两点沿原来的方向继续前进.又经历了99次相遇后停止运动,请问此时两点停在长方形ABCD边上的什么位置?
23.小明用8个完全相同的小长方形拼图,拼出了如图甲、乙的两种图案:图案甲是一个正方形,图案乙是一个大的长方形;图案甲的中间留下了边长是1的正方形小洞.
(1)设每个小方形的宽为x,由图乙可知每个小长方形的长可表示为 .
(2)求小长方形的长和宽.
24.如图,小刚将一个正方形纸片剪去一个宽为5cm的长条后,再从剩下的长方形纸片上剪去一个宽为6cm的长条.如果两次剪下的长条面积正好相等,求两个所剪下的长条的面积之和.
答案
一、选择题.
C.A.C.C.B.A.D.A.C.C.
二、填空题
11.12
12.2000
13.a.
14.12.
15.
16.5cm.
17.36.
18.8.
三、解答题
19.解:∵甲、乙两种作物的单位面积产量的比是1:2,
∴要使甲、乙两种作物的总产量的比是 3:4,
则设种植甲作物的面积为:x,种植乙作物的面积为:(20000﹣x),
∴:1:2,
解得:x=12000,
∴种植乙作物的面积为:20000﹣12000=8000,
分法:
甲的种植长度为120,宽度100,或者长度为200,宽度为60;
乙的种植长度100,宽度80或者长度200,宽度为40
即可得出符合要求的两部分.
20.解:(1)若设图中最大正方形B的边长是x米,最小的正方形的边长是1米.
F的边长为(x﹣1)米,
C的边长为,
E的边长为(x﹣1﹣1);
(2)∵MQ=PN,
∴x﹣1+x﹣2=x,
x=7,
x的值为7;
(3)设余下的工程由乙队单独施工,还要x天完成.
()×2x=1,
x=10(天).
答:余下的工程由乙队单独施工,还要10天完成.
21.解:设图中最大正方形B的边长是x米,
∵最小的正方形的边长是2米,
∴正方形F的边长为(x﹣2)米,正方形E的边长为(x﹣4)米,正方形C的边长为米.
∵MQ=PN,
∴x﹣2+x﹣4=x米,
解得:x=14.
则QM=12+10=22(米),PQ=12+14=26(米)
故该花园的总面积=22×26=572(平方米).
答:该花园的总面积是572平方米.
22.解:(1)设点P原来的速度为xcm/s,根据题意得,
,
解得,x,
经检验,x是原方程的解,
故答案为:;
(2)设P、Q两点在B点处首次相遇后,再经过y秒后第二次在E点相遇,根据题意得,
,
解得,y=3,
故答案为:3;
(3)由(2)知,B到E点的路程长度为:(cm),
∵10﹣AB=10﹣4=6<AD,
∴E点在AD边上,且AE=6(cm),
∴DE=AD﹣AE=8﹣6=2(cm),
∴(cm2),
故答案为:AD;4;
(4)由(3)知,当P、Q相遇一次,则Q行驶(cm),
由由此知得,如下图,E1、E2、E3…,依次为P、Q相遇第一次、第二次、第三次…的位置,
由上可知,P、Q两点每相遇12次,就与前面12个位置依次重复,
∵99÷12=8…3,
∴P、Q两点经历了99次相遇后停止的位置在E3处,
∴P、Q两点经历了99次相遇后停止,此时两点停在长方形ABCD边上的C点位置.
23.解:(1)由题意知,每个小长方形的长为:.
故答案是:.
(2)依题意,得.
解得x=3.
答:每个小长方形的长为5,宽为3.
24.解:设原来正方形纸的边长是xcm,则第一次剪下的长条的长是xcm,宽是5cm,第二次剪下的长条的长是(x﹣5)cm,宽是6cm,
则5x=6(x﹣5),
解得:x=30
30×5×2=300(cm2),
答:两个所剪下的长条的面积之和为300cm2.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
