多项式与多项式相乘
图片预览






文档简介
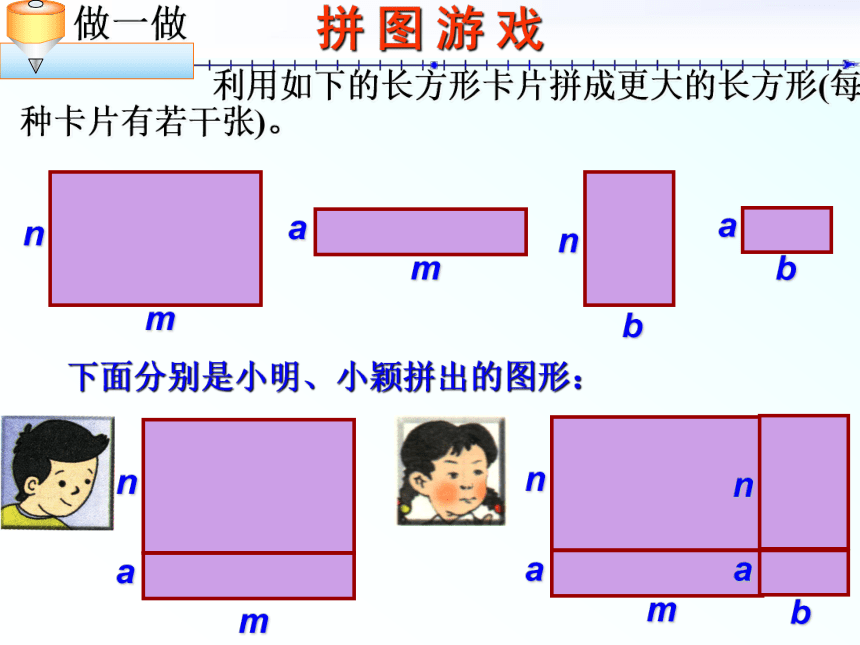
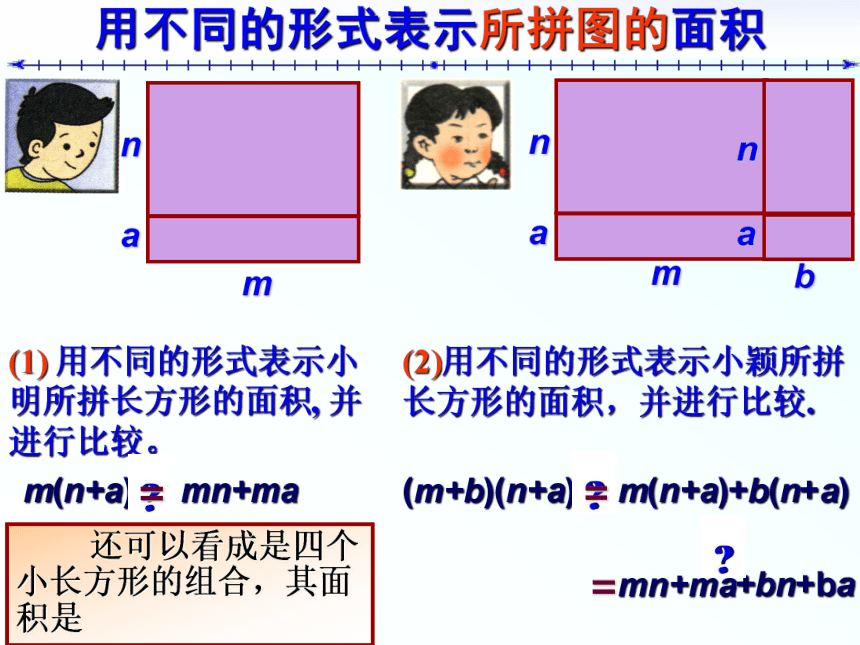
课件28张PPT。 8.2整式乘法多项式与多项式相乘回顾与思考?② 再把所得的积相加。① 用单项式分别去乘多项式的每一项,单项式乘以多项式的依据是 乘法对加法的分配律.① 不能漏乘:即单项式要乘遍多项式的每一项.② 去括号时注意符号的确定.拼 图 游 戏 利用如下的长方形卡片拼成更大的长方形(每种卡片有若干张)。mnmabnba下面分别是小明、小颖拼出的图形:用不同的形式表示所拼图的面积(1) 用不同的形式表示小明所拼长方形的面积, 并进行比较。m(n+a)(2)用不同的形式表示小颖所拼长方形的面积,并进行比较.mn+ma=(m+b)(n+a)m(n+a)+b(n+a)mn+ma+bn+ba==可以看成是小明拼的图形与另一个长方形的组合,其面积是 还可以看成是四个小长方形的组合,其面积是(m+b)(n+a)=m(n+a) + b(n+a) 的 理解(m+b)(n+a)、m(n+a)+b(n+a) ,
这些不同的式子都表示了最大
的长方形的面积,应该相等。 能用
“单项式乘以多项式”
来理解这两个式子的相等吗??我们早已具备了“用字母表示数”概念,
故“x”可以表示一个数。“x”还可以表示 。一个单项式一个多项式将等号两端的 x换成(n+a)则有:(n+a)(n+a)(n+a)用乘法分配律 完成(m+b)(n+a)的计算把 (n+a) 看成
单项式, 把(m+b)看成多项式,
运用单项式乘多项式的法则,(m+b)(n+a)=m(n+a) + b(n+a) 可得:=mn+ma++bn+bamn+ ma+ ma+ bn+ bn 如何进行多项式与多项式相乘的 运算 ? 先用一个多项式的每一项去
乘另一个多项式的每一项再把所得的积相加。(m+b)(n+a)=m(n+a) + b (n+a)mn+ ma+ ma+ bn+ bn动动手解:解:原式=解:原式=例题解析例题解析 【例3】计算: 阅读 ? 体验 ? (1)(1?x)(0.6?x); (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定:??1?x?x? 0.6+=0.6?1.6x+x2 ; ??x? x负负得正
一正一负得负。(2) (2x + y)(x?y)=2xx2x?x2x?y?2x? y+ y+ y? x+??y?y=2x2?2xy+ xy?y2=2x2 ?xy?y2. ?最后的结果要合并同类项. 随堂练习(1)(m+2n)(m?2n); (2)(2n +5)(n?3) ;1、计算:(3)(x+2y)2 ; (4)(ax+b)(cx+d ) .解:原式=解:原式=解:原式=解:原式=计算:(1) (3x+2y)( x-5y)
(2)(x+y)(x2-xy+y2)
(3)(x+2)(x+4)-x(x+1)-8
(4)3(x-2)(x+1)-2(x-5)(x-3)多项式与多项式相乘计算:再显身手判别下列解法是否正确,若错请说出理由。解:原式判别下列解法是否正确,若错请说出理由.解:原式判别下列解法是否正确,若错请说出理由。解:原式注 意 !1.计算(2a+b)2应该这样做:
(2a+b)2=(2a+b)(2a+b)
=4a2+2ab+2ab+b2
=4a2+4ab+b2
切记 一般情况下
(2a+b)2不等于4a2+b2 .注 意 !2.(3a–2)(a–1)–(a+1)(a+2)是多项式的积与积的差,后两个多项式乘积的展开式要用括号括起来。
3. (x+y)(2x–y)(3x+2y)是三个多项式相乘,应该选其中的两个先相乘,把它们的积用括号括起来,再与第三个相乘。 运算结果不是最简形式 【例3】 计算:
x(x2+3)+x2(x-3)-3x(x2-x-1). 错解:
x(x2+3)+x2(x-3)-3x(x2-x-1) =x3+3x+x3-3x-3x3+3x2+3x. 剖析:本题在运用法则运算时并没有错,问题出在其结果没有合并同类项. 正解:
x(x2+3)+x2(x-3)-3x(x2-x-1) =x3+3x+x3-3x2-3x3+3x2+3x=-x3+6x. . 四、顺序混乱 【例4】计算:(a+2)(3-a). 错解:(a+2)(3-a)=3a-2a+a2+6=a2+a+6. 分析:此题错解中,一是有符号错误,误将“-”写成“+”;二是方法不当,是指这里计算顺序混乱,这样容易出错.应根据多项式的乘法法则计算. 正解:(a+2)(3-a)=3a-a2+6-2a=-a2+a+6解方程:
(1)(2x+3)(x-4)-(x+2)(x-2)=x2+7
(2) (3x-2)(2x-3)=(6x+5)(x-1)-1 【例4】阅读下列解答过程,并回答问题:在(x2+ax+b)(2x2-3x-1)的积中,x3的系数为
-5,x2的系数为-6,求a、b. 解:(x2+ax+b)(2x2-3x-1) =2x4-3x3+2ax3-3ax2+2bx2-3bx ① =2x 4-(3-2a)x 3-(3a-2b)x 2-3bx ②
根据对应项系数相等,有解得回答:(1)上述解答过程是否正确?(2)若不正确,从第___步开始出错的,其他步骤是否还有错误? (3)写出正确的解答过程:_____.
计算:
1.(1)(3x-2y)(2x+3y)
(2)(x+2)(x+3)-(x+6)(x-1)
(3)(3x2+2x+1)(2x2+3x-1)
(4)(3x+2y)(2x+3y)-(x-3y)(3x+4y)
2.已知多项式(mx+8)(2-3x)展开后不含x项,求m的值本节课你的收获是什么?小结本节课你学到了什么?多项式乘以多项式的 依据是什么?如何进行多项式与多项式乘法运算?运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.最后的计算结果要化简 ̄ ̄ ̄合并同类项. 活动与探索填空: 观察上面四个等式,你能发现什么规律?-24-24 含有相同字母的两个一次二项式的乘积,是同一个字母的二次三项式 :二次项是这个相同字母的平方(x2);一次项系数是两个常数的和,常数项是两个常数的积.(x+a)(x+b)=x2+(a+b)x+ab
这些不同的式子都表示了最大
的长方形的面积,应该相等。 能用
“单项式乘以多项式”
来理解这两个式子的相等吗??我们早已具备了“用字母表示数”概念,
故“x”可以表示一个数。“x”还可以表示 。一个单项式一个多项式将等号两端的 x换成(n+a)则有:(n+a)(n+a)(n+a)用乘法分配律 完成(m+b)(n+a)的计算把 (n+a) 看成
单项式, 把(m+b)看成多项式,
运用单项式乘多项式的法则,(m+b)(n+a)=m(n+a) + b(n+a) 可得:=mn+ma++bn+bamn+ ma+ ma+ bn+ bn 如何进行多项式与多项式相乘的 运算 ? 先用一个多项式的每一项去
乘另一个多项式的每一项再把所得的积相加。(m+b)(n+a)=m(n+a) + b (n+a)mn+ ma+ ma+ bn+ bn动动手解:解:原式=解:原式=例题解析例题解析 【例3】计算: 阅读 ? 体验 ? (1)(1?x)(0.6?x); (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定:??1?x?x? 0.6+=0.6?1.6x+x2 ; ??x? x负负得正
一正一负得负。(2) (2x + y)(x?y)=2xx2x?x2x?y?2x? y+ y+ y? x+??y?y=2x2?2xy+ xy?y2=2x2 ?xy?y2. ?最后的结果要合并同类项. 随堂练习(1)(m+2n)(m?2n); (2)(2n +5)(n?3) ;1、计算:(3)(x+2y)2 ; (4)(ax+b)(cx+d ) .解:原式=解:原式=解:原式=解:原式=计算:(1) (3x+2y)( x-5y)
(2)(x+y)(x2-xy+y2)
(3)(x+2)(x+4)-x(x+1)-8
(4)3(x-2)(x+1)-2(x-5)(x-3)多项式与多项式相乘计算:再显身手判别下列解法是否正确,若错请说出理由。解:原式判别下列解法是否正确,若错请说出理由.解:原式判别下列解法是否正确,若错请说出理由。解:原式注 意 !1.计算(2a+b)2应该这样做:
(2a+b)2=(2a+b)(2a+b)
=4a2+2ab+2ab+b2
=4a2+4ab+b2
切记 一般情况下
(2a+b)2不等于4a2+b2 .注 意 !2.(3a–2)(a–1)–(a+1)(a+2)是多项式的积与积的差,后两个多项式乘积的展开式要用括号括起来。
3. (x+y)(2x–y)(3x+2y)是三个多项式相乘,应该选其中的两个先相乘,把它们的积用括号括起来,再与第三个相乘。 运算结果不是最简形式 【例3】 计算:
x(x2+3)+x2(x-3)-3x(x2-x-1). 错解:
x(x2+3)+x2(x-3)-3x(x2-x-1) =x3+3x+x3-3x-3x3+3x2+3x. 剖析:本题在运用法则运算时并没有错,问题出在其结果没有合并同类项. 正解:
x(x2+3)+x2(x-3)-3x(x2-x-1) =x3+3x+x3-3x2-3x3+3x2+3x=-x3+6x. . 四、顺序混乱 【例4】计算:(a+2)(3-a). 错解:(a+2)(3-a)=3a-2a+a2+6=a2+a+6. 分析:此题错解中,一是有符号错误,误将“-”写成“+”;二是方法不当,是指这里计算顺序混乱,这样容易出错.应根据多项式的乘法法则计算. 正解:(a+2)(3-a)=3a-a2+6-2a=-a2+a+6解方程:
(1)(2x+3)(x-4)-(x+2)(x-2)=x2+7
(2) (3x-2)(2x-3)=(6x+5)(x-1)-1 【例4】阅读下列解答过程,并回答问题:在(x2+ax+b)(2x2-3x-1)的积中,x3的系数为
-5,x2的系数为-6,求a、b. 解:(x2+ax+b)(2x2-3x-1) =2x4-3x3+2ax3-3ax2+2bx2-3bx ① =2x 4-(3-2a)x 3-(3a-2b)x 2-3bx ②
根据对应项系数相等,有解得回答:(1)上述解答过程是否正确?(2)若不正确,从第___步开始出错的,其他步骤是否还有错误? (3)写出正确的解答过程:_____.
计算:
1.(1)(3x-2y)(2x+3y)
(2)(x+2)(x+3)-(x+6)(x-1)
(3)(3x2+2x+1)(2x2+3x-1)
(4)(3x+2y)(2x+3y)-(x-3y)(3x+4y)
2.已知多项式(mx+8)(2-3x)展开后不含x项,求m的值本节课你的收获是什么?小结本节课你学到了什么?多项式乘以多项式的 依据是什么?如何进行多项式与多项式乘法运算?运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.最后的计算结果要化简 ̄ ̄ ̄合并同类项. 活动与探索填空: 观察上面四个等式,你能发现什么规律?-24-24 含有相同字母的两个一次二项式的乘积,是同一个字母的二次三项式 :二次项是这个相同字母的平方(x2);一次项系数是两个常数的和,常数项是两个常数的积.(x+a)(x+b)=x2+(a+b)x+ab
