1.4.1用空间向量研究直线与平面位置关系(第一课时) 课件(共19张PPT)
文档属性
| 名称 | 1.4.1用空间向量研究直线与平面位置关系(第一课时) 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 15:38:38 | ||
图片预览


文档简介
(共19张PPT)
1.4.1 用空间向量研究
直线、平面的位置关系
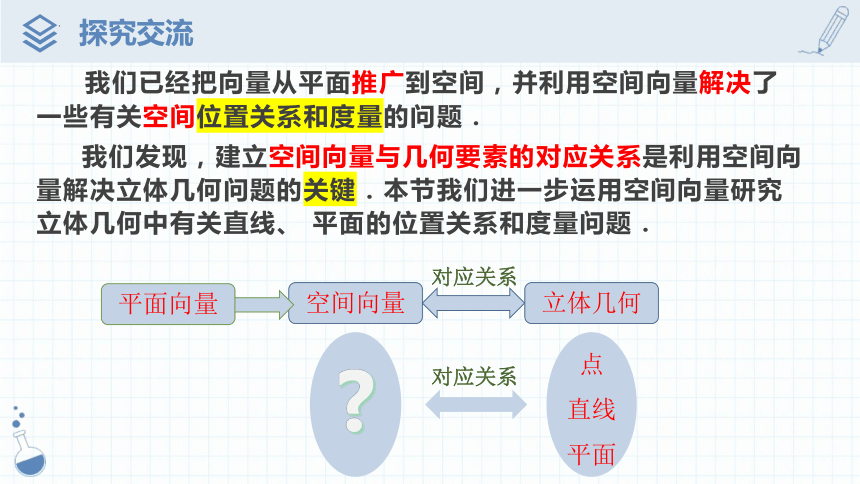
我们已经把向量从平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题.
我们发现,建立空间向量与几何要素的对应关系是利用空间向量解决立体几何问题的关键.本节我们进一步运用空间向量研究立体几何中有关直线、 平面的位置关系和度量问题.
对应关系
点
直线
平面
对应关系
空间向量
立体几何
平面向量
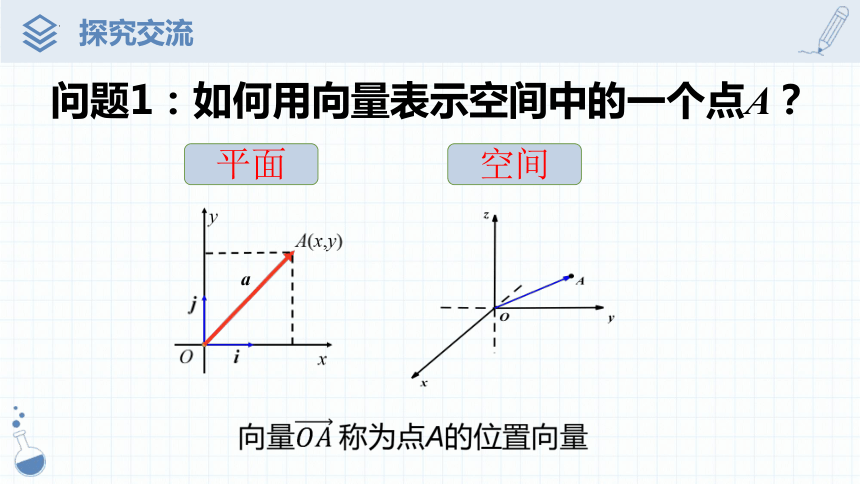
问题1:如何用向量表示空间中的一个点A?
平面
空间
向量称为点A的位置向量
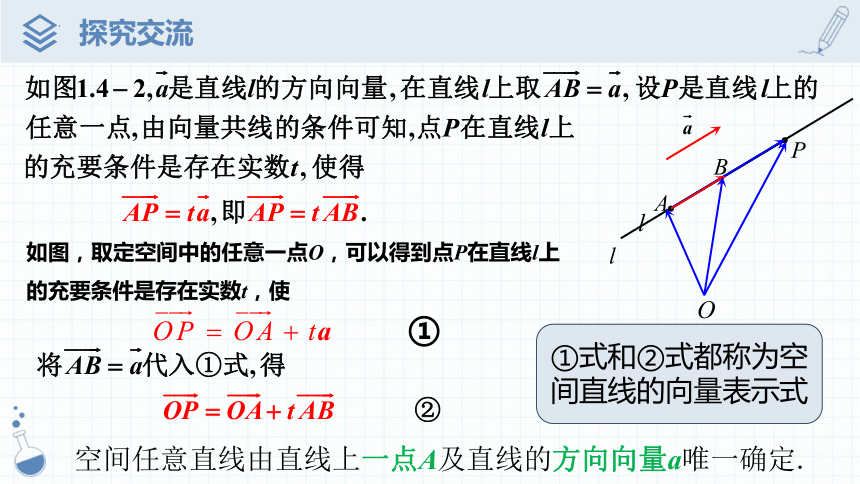
问题2:如何用向量表示空间中的直线l?
追问1 :两点确定一条直线,故可以确定直线l吗?
只可以确定直线l的方向为直线l的方向向量
追问2:我们知道空间中给定一个定点A和一个方向可以唯一确定一条直线l.如何用向量表示直线l?
是直线l的方向向量,定点A
用向量表示直线l , 就是要利用点A和直线l的方向向量表示直线上的任意一点.
A
B
P
l
O
l
如图,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使
①
①式和②式都称为空间直线的向量表示式
空间任意直线由直线上一点A及直线的方向向量a唯一确定.
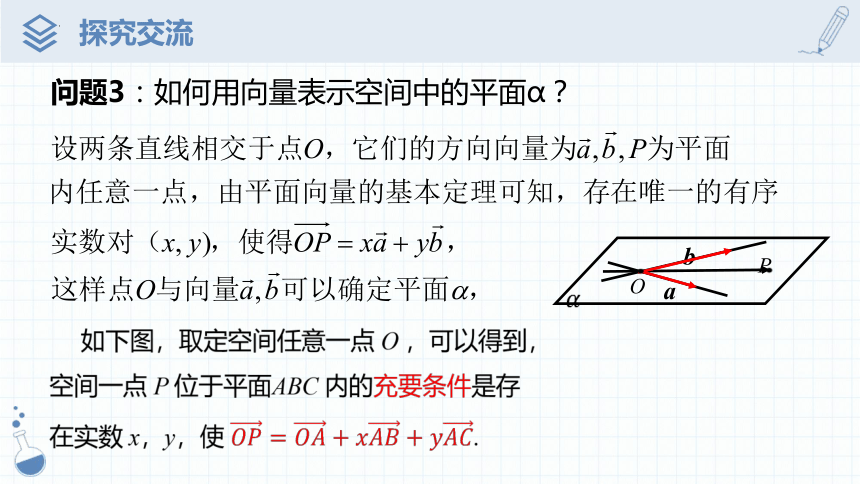
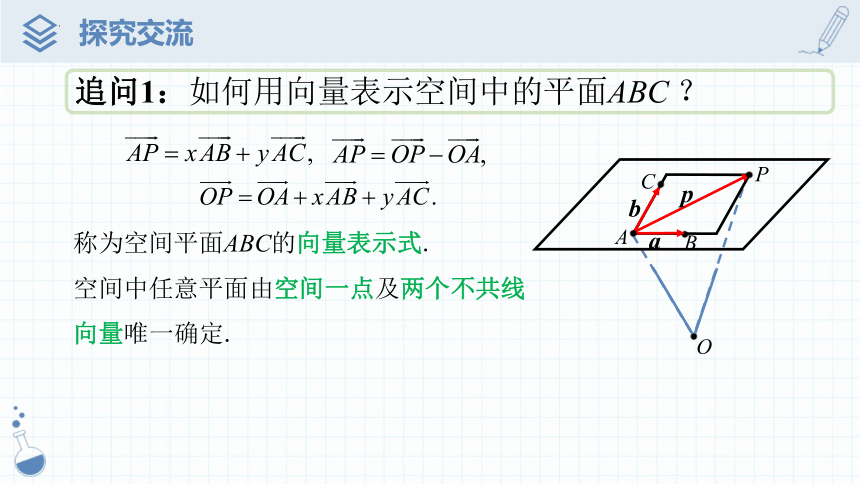
问题3:如何用向量表示空间中的平面α?
b
P
O
a
如下图,取定空间任意一点 O ,可以得到,空间一点 P 位于平面ABC 内的充要条件是存在实数 x,y,使 .
追问1:如何用向量表示空间中的平面ABC ?
A
C
B
a
O
b
P
p
称为空间平面ABC的向量表示式.
空间中任意平面由空间一点及两个不共线向量唯一确定.
追问2:如何用一个向量表示空间中的平面 ?
直线 , 取直线l的方向向量a, 我们称向量a为平面的法向量(normal vector).
l
a
A
给定一个点A和一个向量a,
那么过点A,且以向量a为法向量的平面,可以表示为集合
追问3:如果另有一条直线 m⊥α,在直线m上任取向量b,b与a有什么关系?
因为 ,
所以 l // m.
所以 a // b.
所以 使得
l
a
m
b
P28-例1.已知长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,(1)求直线CD的方向向量.(2)求平面BCC1B1的一个法向量.(3)求平面MCA1的一个法向量.
解:(1)由题可知D(0,0,0),C(0,4,0),
追问1:直线CD还有其他的方向向量吗?
追问2:(0,1,0),(0,a,0)是直线CD的方向向量吗?
(0,a,0)(a≠0)
P28-例1.已知长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,(2)求平面BCC1B1的一个法向量.
追问1:平面BCC1B1还有其他的法向量吗?
追问2:(0,1,0),(0,a,0)是平面BCC1B1的法向量吗?
(0,a,0)(a≠0)
解:由题DC⊥平面BCC1B1,平面BCC1B1的一个法向量
定义法
P28-例1.已知长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系 (3)求平面MCA1的一个法向量.
设法向量
找两向量
列方程组
赋非零值
下结论
待定系数法
①定义法(找线面垂直)
②待定系数法(设/列/赋)
(1)同一条直线的方向向量有无穷多个,它们互相平行.(2)同一个平面的法向量有无穷多个,它们互相平行.
(3)直线方向向量和平面法向量的求法:
向量的名称 图示 求法
①找到l⊥α;
②l的方向向量即为平面的法向量
①取两点;②定向量
①设面α的法向量;②求面α内的不共线向量;③列方程组;④解方程组,得出结论
平面的法向量
直线的方向向量
A
B
n
练习(第29页)
√
√
×
A
B
C
D
D1
A1
B1
C1
O
A
B
C
D
D1
A1
B1
C1
x
y
z
建系
找两向量
设法向量
列方程组
赋非零值
下结论
1.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,求平面PAD和平面EDB的法向量.
x
y
z
定义法
待定系数法
①定义法(找线面垂直)
②待定系数法(设/列/赋)
教科书习题1.4第1,2题.
用向量表示点:
用向量表示直线:
用向量表示平面:
, 其中a是平面的法向量.
求直线方向向量和平面法向量的方法
求平面法向量的步骤
1.4.1 用空间向量研究
直线、平面的位置关系
我们已经把向量从平面推广到空间,并利用空间向量解决了一些有关空间位置关系和度量的问题.
我们发现,建立空间向量与几何要素的对应关系是利用空间向量解决立体几何问题的关键.本节我们进一步运用空间向量研究立体几何中有关直线、 平面的位置关系和度量问题.
对应关系
点
直线
平面
对应关系
空间向量
立体几何
平面向量
问题1:如何用向量表示空间中的一个点A?
平面
空间
向量称为点A的位置向量
问题2:如何用向量表示空间中的直线l?
追问1 :两点确定一条直线,故可以确定直线l吗?
只可以确定直线l的方向为直线l的方向向量
追问2:我们知道空间中给定一个定点A和一个方向可以唯一确定一条直线l.如何用向量表示直线l?
是直线l的方向向量,定点A
用向量表示直线l , 就是要利用点A和直线l的方向向量表示直线上的任意一点.
A
B
P
l
O
l
如图,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使
①
①式和②式都称为空间直线的向量表示式
空间任意直线由直线上一点A及直线的方向向量a唯一确定.
问题3:如何用向量表示空间中的平面α?
b
P
O
a
如下图,取定空间任意一点 O ,可以得到,空间一点 P 位于平面ABC 内的充要条件是存在实数 x,y,使 .
追问1:如何用向量表示空间中的平面ABC ?
A
C
B
a
O
b
P
p
称为空间平面ABC的向量表示式.
空间中任意平面由空间一点及两个不共线向量唯一确定.
追问2:如何用一个向量表示空间中的平面 ?
直线 , 取直线l的方向向量a, 我们称向量a为平面的法向量(normal vector).
l
a
A
给定一个点A和一个向量a,
那么过点A,且以向量a为法向量的平面,可以表示为集合
追问3:如果另有一条直线 m⊥α,在直线m上任取向量b,b与a有什么关系?
因为 ,
所以 l // m.
所以 a // b.
所以 使得
l
a
m
b
P28-例1.已知长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,(1)求直线CD的方向向量.(2)求平面BCC1B1的一个法向量.(3)求平面MCA1的一个法向量.
解:(1)由题可知D(0,0,0),C(0,4,0),
追问1:直线CD还有其他的方向向量吗?
追问2:(0,1,0),(0,a,0)是直线CD的方向向量吗?
(0,a,0)(a≠0)
P28-例1.已知长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,(2)求平面BCC1B1的一个法向量.
追问1:平面BCC1B1还有其他的法向量吗?
追问2:(0,1,0),(0,a,0)是平面BCC1B1的法向量吗?
(0,a,0)(a≠0)
解:由题DC⊥平面BCC1B1,平面BCC1B1的一个法向量
定义法
P28-例1.已知长方体ABCD-A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系 (3)求平面MCA1的一个法向量.
设法向量
找两向量
列方程组
赋非零值
下结论
待定系数法
①定义法(找线面垂直)
②待定系数法(设/列/赋)
(1)同一条直线的方向向量有无穷多个,它们互相平行.(2)同一个平面的法向量有无穷多个,它们互相平行.
(3)直线方向向量和平面法向量的求法:
向量的名称 图示 求法
①找到l⊥α;
②l的方向向量即为平面的法向量
①取两点;②定向量
①设面α的法向量;②求面α内的不共线向量;③列方程组;④解方程组,得出结论
平面的法向量
直线的方向向量
A
B
n
练习(第29页)
√
√
×
A
B
C
D
D1
A1
B1
C1
O
A
B
C
D
D1
A1
B1
C1
x
y
z
建系
找两向量
设法向量
列方程组
赋非零值
下结论
1.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,求平面PAD和平面EDB的法向量.
x
y
z
定义法
待定系数法
①定义法(找线面垂直)
②待定系数法(设/列/赋)
教科书习题1.4第1,2题.
用向量表示点:
用向量表示直线:
用向量表示平面:
, 其中a是平面的法向量.
求直线方向向量和平面法向量的方法
求平面法向量的步骤
