1.4.2用空间向量研究距离夹角问题(第二课时角度-线线、线面角) 课件(共15张PPT)
文档属性
| 名称 | 1.4.2用空间向量研究距离夹角问题(第二课时角度-线线、线面角) 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 15:40:05 | ||
图片预览






文档简介
(共15张PPT)
1.4.2 用空间向量研究距离、夹角问题
第二课时
导入问题:与距离一样,角度是立体几何中的另一类度量问题.本质上,角度是对两个方向的差的度量,向量是有方向的量,所以利用向量研究角度问题有其独特的优势.本节我们用空间向量研究夹角问题,你认为可以按怎样的顺序展开研究.
空间向量
立体几何
距离问题
夹角问题
问题1:如何利用空间向量研究角度问题?
直线与直线所成的角
直线与平面所成的角
平面与平面所成的角
直线方向向量的夹角
方向向量与法向量的夹角
法向量的夹角
追问1:两条直线夹角的定义是什么?
//
规定与的夹角为
追问2:两条直线夹角的取值范围是什么?
平面内,两条直线, 相交向形成4个角,其中不大于90°的角称为两条直线与 成的角(或夹角).
空间中,两条异面直线, ,经过空间任一点O分别做直线’ ∥ , ’ ∥ ,我们把直线’与’所成的角叫做异面直线与 成的角(或夹角).
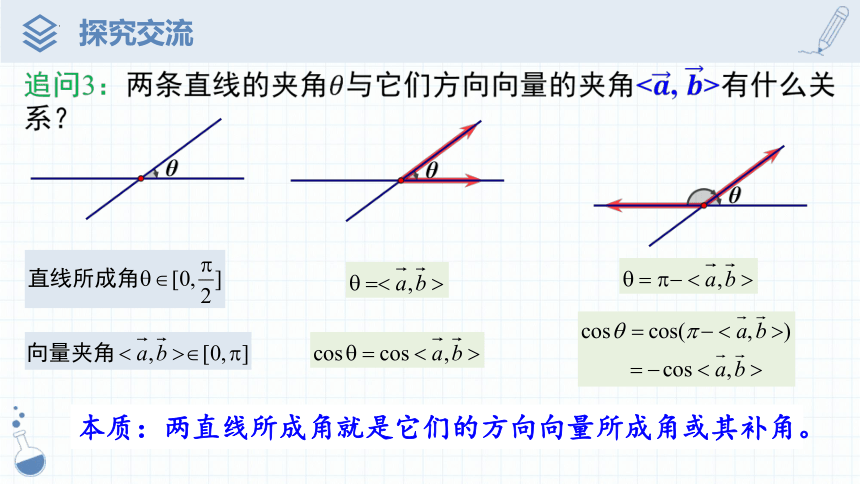
追问3:两条直线的夹角与它们方向向量的夹角<, >有什么关系?
本质:两直线所成角就是它们的方向向量所成角或其补角。
A
B
C
D
M
N
追问1:这个问题的已知条件是什么?根据以往的经验,你打算通过什么途径将这个立体几何问题转化成向量问题?
基底法
几何法
坐标法
向量与的夹角
设向量与的夹角为,则直线与夹角的余弦值等于.
解:以{,}为基底【基底选择不唯一】
又
所以直线夹角的余弦值等于
追问1:这个问题的已知条件是什么?根据以往的经验,你打算通过什么途径将这个立体几何问题转化成向量问题?
基底法
几何法
坐标法
向量与的夹角
解:取中点,过作⊥平面,
以为原点,,,所在直线为轴、轴、轴,建立如图所示的空间直角坐标系.
请同学们课后完成!
将立体几何问题转化成向量问题的途径:
途径1:通过建立一个基底,用空间向量表示问题中涉及的点、直线、平面等元素,从而把立体几何问题转化成向量问题;
途径2:通过建立空间直角坐标系,用坐标表示问题中涉及的点、直线、平面等元素,从而把立体几何问题转化成向量问题.
实际上,空间直角坐标系也是基底,是“特殊”的基底.
用空间向量求两条直线,夹角的步骤与方法:
化为向量问题
进行向量运算
①转化为求两直线,的方向向量,的夹角
回到图形问题
③两条直线,夹角的余弦值
问题2:如何利用向量求直线到平面的夹角?
两条直线夹角的定义
两条直线夹角的取值范围
两条直线夹角的向量求法
直线与平面所成角的定义
直线与平面所成角的取值范围
直线与平面所成角的向量求法
直线与平面所成角问题的研究路径:
问题2:如何直线与平面夹角的定义范围?
α
θ=0°
⊥α
θ=90°
∥α
θ=0°
α的斜线
0°<θ<90°
追问1:直线与平面的夹角与有什么关系?
若直线a的方向向量分别为,平面α的法向量为
本质:直线与平面所成角就是它们的方向向量所成角减去90°或其余角。
基底法
几何法
坐标法
求直线与平面所成角
角的正弦值.
向量与平面的法向量的夹角
所以直线与平面所成的角正弦值等于
用空间向量求直线平面所成角的步骤和方法:
化为向量问题
进行向量运算
回到图形问题
①转化为求直线的方向向量与平面法向量的夹角
③直线平面所成的角的 正弦值
角的类型 角的取值范围 方向向量 与法向量 与向量夹角的关系
两条直线的夹角 两条直线的方向向量
直线与平面所成的角 直线的方向向量, 平面的法向量
1.4.2 用空间向量研究距离、夹角问题
第二课时
导入问题:与距离一样,角度是立体几何中的另一类度量问题.本质上,角度是对两个方向的差的度量,向量是有方向的量,所以利用向量研究角度问题有其独特的优势.本节我们用空间向量研究夹角问题,你认为可以按怎样的顺序展开研究.
空间向量
立体几何
距离问题
夹角问题
问题1:如何利用空间向量研究角度问题?
直线与直线所成的角
直线与平面所成的角
平面与平面所成的角
直线方向向量的夹角
方向向量与法向量的夹角
法向量的夹角
追问1:两条直线夹角的定义是什么?
//
规定与的夹角为
追问2:两条直线夹角的取值范围是什么?
平面内,两条直线, 相交向形成4个角,其中不大于90°的角称为两条直线与 成的角(或夹角).
空间中,两条异面直线, ,经过空间任一点O分别做直线’ ∥ , ’ ∥ ,我们把直线’与’所成的角叫做异面直线与 成的角(或夹角).
追问3:两条直线的夹角与它们方向向量的夹角<, >有什么关系?
本质:两直线所成角就是它们的方向向量所成角或其补角。
A
B
C
D
M
N
追问1:这个问题的已知条件是什么?根据以往的经验,你打算通过什么途径将这个立体几何问题转化成向量问题?
基底法
几何法
坐标法
向量与的夹角
设向量与的夹角为,则直线与夹角的余弦值等于.
解:以{,}为基底【基底选择不唯一】
又
所以直线夹角的余弦值等于
追问1:这个问题的已知条件是什么?根据以往的经验,你打算通过什么途径将这个立体几何问题转化成向量问题?
基底法
几何法
坐标法
向量与的夹角
解:取中点,过作⊥平面,
以为原点,,,所在直线为轴、轴、轴,建立如图所示的空间直角坐标系.
请同学们课后完成!
将立体几何问题转化成向量问题的途径:
途径1:通过建立一个基底,用空间向量表示问题中涉及的点、直线、平面等元素,从而把立体几何问题转化成向量问题;
途径2:通过建立空间直角坐标系,用坐标表示问题中涉及的点、直线、平面等元素,从而把立体几何问题转化成向量问题.
实际上,空间直角坐标系也是基底,是“特殊”的基底.
用空间向量求两条直线,夹角的步骤与方法:
化为向量问题
进行向量运算
①转化为求两直线,的方向向量,的夹角
回到图形问题
③两条直线,夹角的余弦值
问题2:如何利用向量求直线到平面的夹角?
两条直线夹角的定义
两条直线夹角的取值范围
两条直线夹角的向量求法
直线与平面所成角的定义
直线与平面所成角的取值范围
直线与平面所成角的向量求法
直线与平面所成角问题的研究路径:
问题2:如何直线与平面夹角的定义范围?
α
θ=0°
⊥α
θ=90°
∥α
θ=0°
α的斜线
0°<θ<90°
追问1:直线与平面的夹角与有什么关系?
若直线a的方向向量分别为,平面α的法向量为
本质:直线与平面所成角就是它们的方向向量所成角减去90°或其余角。
基底法
几何法
坐标法
求直线与平面所成角
角的正弦值.
向量与平面的法向量的夹角
所以直线与平面所成的角正弦值等于
用空间向量求直线平面所成角的步骤和方法:
化为向量问题
进行向量运算
回到图形问题
①转化为求直线的方向向量与平面法向量的夹角
③直线平面所成的角的 正弦值
角的类型 角的取值范围 方向向量 与法向量 与向量夹角的关系
两条直线的夹角 两条直线的方向向量
直线与平面所成的角 直线的方向向量, 平面的法向量
