1.4.2用空间向量研究距离夹角问题(第三课时面面角)高中数学人教A版选择性必修1 课件(共18张PPT)
文档属性
| 名称 | 1.4.2用空间向量研究距离夹角问题(第三课时面面角)高中数学人教A版选择性必修1 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 15:40:30 | ||
图片预览




文档简介
(共18张PPT)
1.4.2 用空间向量研究距离、夹角问题
第三课时面面角
α
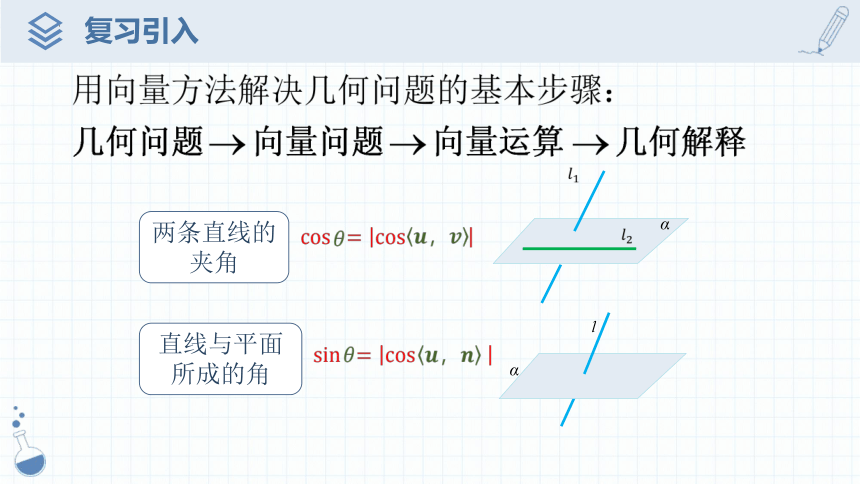
两条直线的夹角
直线与平面所成的角
α
l
问题1:类比直线与直线的夹角的定义,如何定义平面到平面的夹角?
追问1:平面与平面的夹角范围是多少?
空间中,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角成为平面α与平面β的夹角。
所以,两个平面夹角θ 的取值范围为:θ ∈[0°,90°]
追问2:二面角的平面角是如何定义的?
在二面角α-l-β的棱上任取一点O,以O为垂足,在半平面α和β内在点 O 处分别作垂直于棱的射线OA、OB,
则射线OA、OB组成的∠AOB叫做二面角α-l-β的平面角.
所以,二面角的取值范围为: [0°,180°]
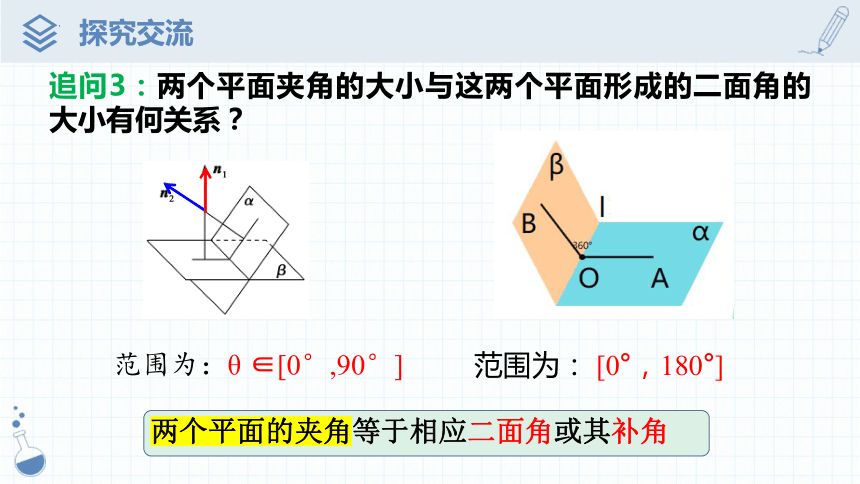
追问3:两个平面夹角的大小与这两个平面形成的二面角的大小有何关系?
范围为:θ ∈[0°,90°]
范围为: [0°,180°]
两个平面的夹角等于相应二面角或其补角
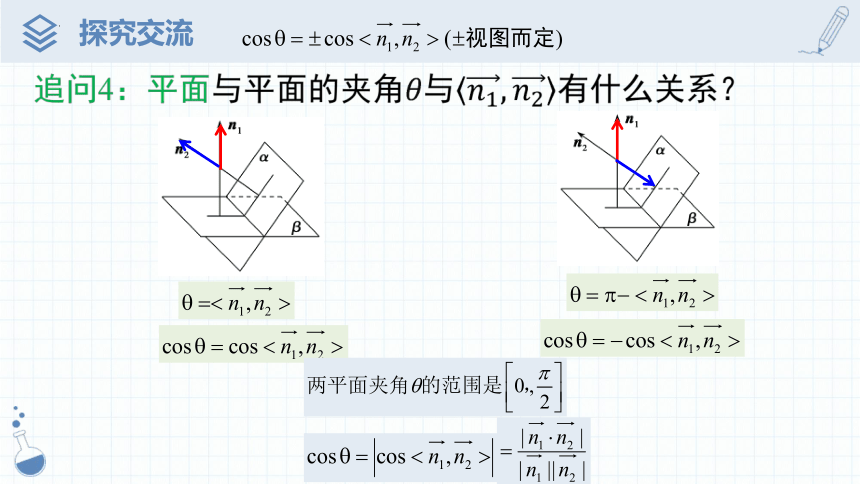
追问4:平面与平面的夹角与有什么关系?
用空间向量求平面与平面所成角的步骤和方法:
化为向量问题
进行向量运算
回到图形问题
①转化为法向量的夹角
③
A
B
C
C1
A1
B1
x
y
z
P
Q
R
解:以为原点,,,所在直线为轴、轴、轴,建立如图所示的空间直角坐标系.
设平面的法向量为,
平面的法向量为,
则平面与平面的夹角就是与的夹角或其补角.
因为平面,
所以平面的一个法向量为.
设平面的法向量为
因为,,,
所以, .
又
所以
所以 取 (3,4,2),
设平面与平面的夹角为,
则
设直线a与b的方向向量分别为,,平面α与平面β的法向量分别为,
求法:先求两向量夹角余弦值→设空间角为θ→下结论(取绝对值or定正负)
A
A1
B1
C1
C
B
x
y
z
O
H
A
B
C
C1
B1
A1
F1
D1
x
y
z
练习(第38页)
A
A
B
C
C1
B1
A1
F1
D1
H
z
P
B
O
A
C
x
y
C
P
B
O
A
C
x
y
z
1.4.2 用空间向量研究距离、夹角问题
第三课时面面角
α
两条直线的夹角
直线与平面所成的角
α
l
问题1:类比直线与直线的夹角的定义,如何定义平面到平面的夹角?
追问1:平面与平面的夹角范围是多少?
空间中,平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角成为平面α与平面β的夹角。
所以,两个平面夹角θ 的取值范围为:θ ∈[0°,90°]
追问2:二面角的平面角是如何定义的?
在二面角α-l-β的棱上任取一点O,以O为垂足,在半平面α和β内在点 O 处分别作垂直于棱的射线OA、OB,
则射线OA、OB组成的∠AOB叫做二面角α-l-β的平面角.
所以,二面角的取值范围为: [0°,180°]
追问3:两个平面夹角的大小与这两个平面形成的二面角的大小有何关系?
范围为:θ ∈[0°,90°]
范围为: [0°,180°]
两个平面的夹角等于相应二面角或其补角
追问4:平面与平面的夹角与有什么关系?
用空间向量求平面与平面所成角的步骤和方法:
化为向量问题
进行向量运算
回到图形问题
①转化为法向量的夹角
③
A
B
C
C1
A1
B1
x
y
z
P
Q
R
解:以为原点,,,所在直线为轴、轴、轴,建立如图所示的空间直角坐标系.
设平面的法向量为,
平面的法向量为,
则平面与平面的夹角就是与的夹角或其补角.
因为平面,
所以平面的一个法向量为.
设平面的法向量为
因为,,,
所以, .
又
所以
所以 取 (3,4,2),
设平面与平面的夹角为,
则
设直线a与b的方向向量分别为,,平面α与平面β的法向量分别为,
求法:先求两向量夹角余弦值→设空间角为θ→下结论(取绝对值or定正负)
A
A1
B1
C1
C
B
x
y
z
O
H
A
B
C
C1
B1
A1
F1
D1
x
y
z
练习(第38页)
A
A
B
C
C1
B1
A1
F1
D1
H
z
P
B
O
A
C
x
y
C
P
B
O
A
C
x
y
z
