1.4.2用空间向量研究距离、夹角问题 高中数学人教A版选择性必修1 课件(共19张PPT)
文档属性
| 名称 | 1.4.2用空间向量研究距离、夹角问题 高中数学人教A版选择性必修1 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 15:40:54 | ||
图片预览



文档简介
(共19张PPT)
1.4.2 用空间向量研究距离、夹角问题
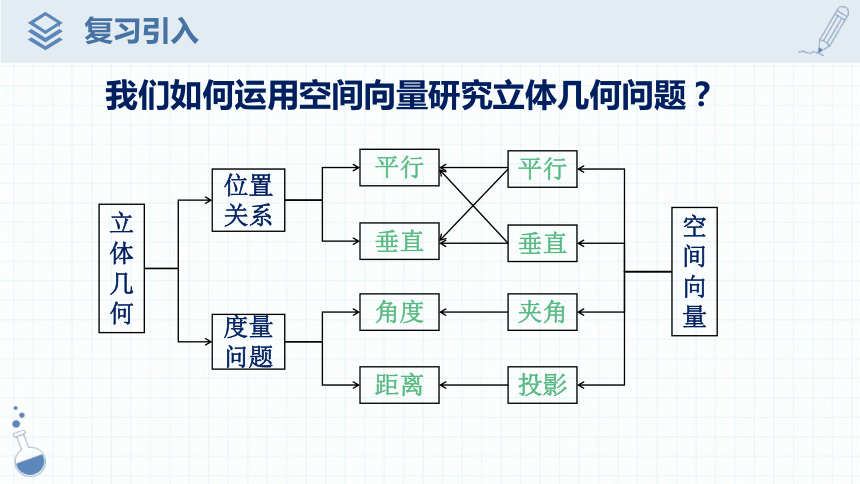
立体几何
度量问题
位置关系
平行
垂直
角度
距离
平行
垂直
夹角
投影
空间向量
我们如何运用空间向量研究立体几何问题?
考点一.求两点距离
①距离公式法(找两点坐标)
②向量求模法(基底法/坐标法)
4
3
5
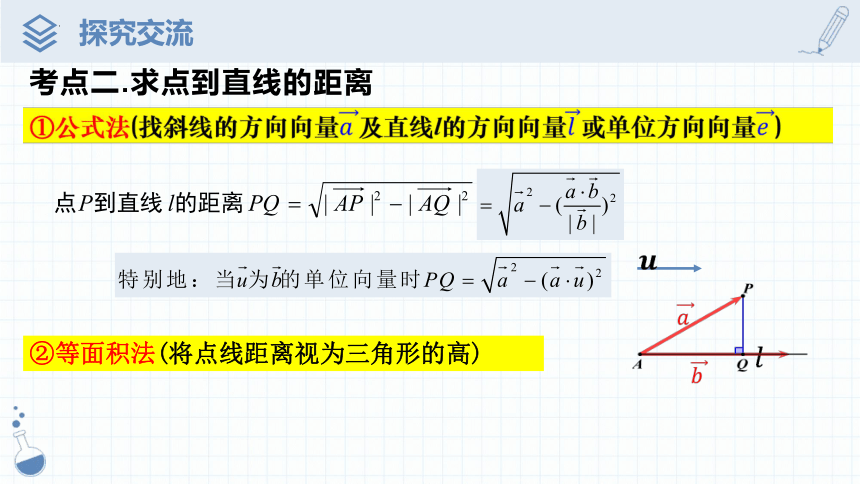
考点二.求点到直线的距离
①公式法(找斜线的方向向量及直线l的方向向量或单位方向向量)
②等面积法(将点线距离视为三角形的高)
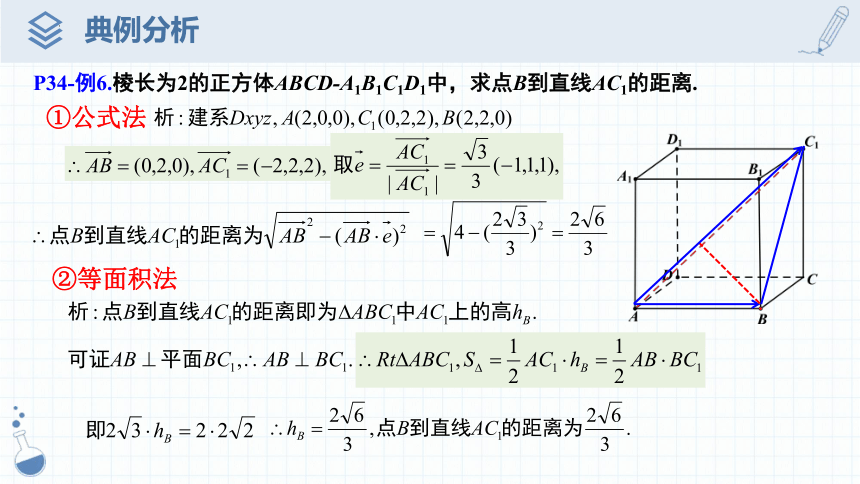
P34-例6.棱长为2的正方体ABCD-A1B1C1D1中,求点B到直线AC1的距离.
①公式法
②等面积法
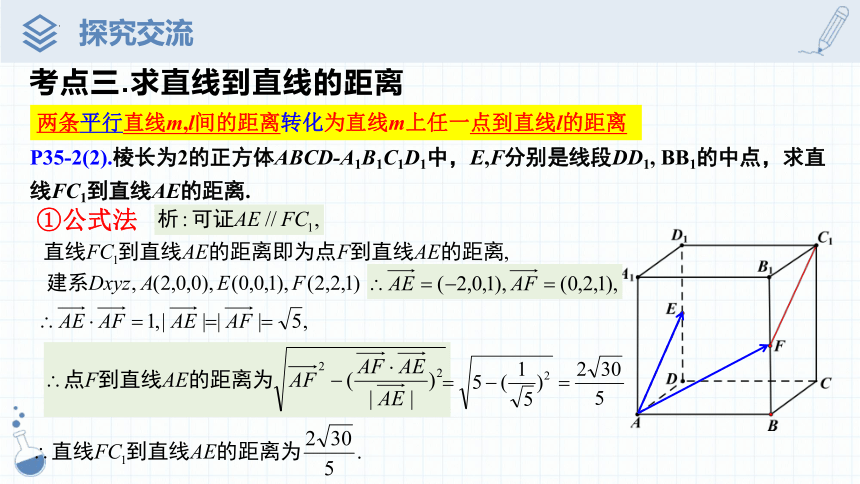
考点三.求直线到直线的距离
两条平行直线m,l间的距离转化为直线m上任一点到直线l的距离
P35-2(2).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1, BB1的中点,求直线FC1到直线AE的距离.
①公式法
考点三.求直线到直线的距离
两条平行直线m,l间的距离转化为直线m上任一点到直线l的距离
P35-2(2).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1, BB1的中点,求直线FC1到直线AE的距离.
②等面积法
M
考点四.求点到面的距离
①公式法(求斜线的方向向量在法向量上的投影向量的模)
②等体积法(将点面距离看作棱锥的高)
P35-2(3).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1的中点,求点A1到平面AEB1的距离.
①公式法
②等体积法
[练习]如图,已知PA⊥平面ABCD且PA=AB,底面ABCD为正方形,设PA=AB=4,求点A到面PDC的距离.
A
B
C
D
E
P
z
x
y
③找垂线法(过点找面的垂线)
考点五.求直线到面的距离
平行于平面的直线到平面的距离转化为线上任意一点到平面的距离
考点六.求面到面的距离
两个平行平面间的距离转化为平面内任意一点到平面的距离
先证线面平行l//α,再转化为直线l上任一点到平面α的距离
先证面面平行α//β,再转化为平面α上任一点到平面β的距离
考点七.求线线角
P41-2.在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,M,N分别为AD、BC的中点,求异面直线AN和CM所成角的余弦值.
设向量与的夹角为,
则直线与夹角的余弦值等于.
解:以{,}为基底【基底选择不唯一】
所以直线夹角的余弦值等于
P41-2.在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,M,N分别为AD、BC的中点,求异面直线AN和CM所成角的余弦值.
P41-2.在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,M,N分别为AD、BC的中点,求异面直线AN和CM所成角的余弦值.
O
M
N
所以直线夹角的余弦值等于
求直线与平面所成角
角的正弦值.
向量与平面的法向量的夹角
所以直线与平面所成的角正弦值等于
考点八.求线面角
①空间向量法
考点八.求线面角
求直线与平面所成角
角的正弦值.
③找垂线法(过点找面的垂线)
②等体积法(将点面距离看作棱锥的高)
A
B
C
D
E
O
N
F
考点九.求面面角
6.在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,E是PD的中点,求平面EAC与平面ABCD的夹角.
几何法
公式法
考点十.证明平行垂直
几何法
向量化
公式法
几何法
向量化
1.4.2 用空间向量研究距离、夹角问题
立体几何
度量问题
位置关系
平行
垂直
角度
距离
平行
垂直
夹角
投影
空间向量
我们如何运用空间向量研究立体几何问题?
考点一.求两点距离
①距离公式法(找两点坐标)
②向量求模法(基底法/坐标法)
4
3
5
考点二.求点到直线的距离
①公式法(找斜线的方向向量及直线l的方向向量或单位方向向量)
②等面积法(将点线距离视为三角形的高)
P34-例6.棱长为2的正方体ABCD-A1B1C1D1中,求点B到直线AC1的距离.
①公式法
②等面积法
考点三.求直线到直线的距离
两条平行直线m,l间的距离转化为直线m上任一点到直线l的距离
P35-2(2).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1, BB1的中点,求直线FC1到直线AE的距离.
①公式法
考点三.求直线到直线的距离
两条平行直线m,l间的距离转化为直线m上任一点到直线l的距离
P35-2(2).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1, BB1的中点,求直线FC1到直线AE的距离.
②等面积法
M
考点四.求点到面的距离
①公式法(求斜线的方向向量在法向量上的投影向量的模)
②等体积法(将点面距离看作棱锥的高)
P35-2(3).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1的中点,求点A1到平面AEB1的距离.
①公式法
②等体积法
[练习]如图,已知PA⊥平面ABCD且PA=AB,底面ABCD为正方形,设PA=AB=4,求点A到面PDC的距离.
A
B
C
D
E
P
z
x
y
③找垂线法(过点找面的垂线)
考点五.求直线到面的距离
平行于平面的直线到平面的距离转化为线上任意一点到平面的距离
考点六.求面到面的距离
两个平行平面间的距离转化为平面内任意一点到平面的距离
先证线面平行l//α,再转化为直线l上任一点到平面α的距离
先证面面平行α//β,再转化为平面α上任一点到平面β的距离
考点七.求线线角
P41-2.在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,M,N分别为AD、BC的中点,求异面直线AN和CM所成角的余弦值.
设向量与的夹角为,
则直线与夹角的余弦值等于.
解:以{,}为基底【基底选择不唯一】
所以直线夹角的余弦值等于
P41-2.在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,M,N分别为AD、BC的中点,求异面直线AN和CM所成角的余弦值.
P41-2.在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,M,N分别为AD、BC的中点,求异面直线AN和CM所成角的余弦值.
O
M
N
所以直线夹角的余弦值等于
求直线与平面所成角
角的正弦值.
向量与平面的法向量的夹角
所以直线与平面所成的角正弦值等于
考点八.求线面角
①空间向量法
考点八.求线面角
求直线与平面所成角
角的正弦值.
③找垂线法(过点找面的垂线)
②等体积法(将点面距离看作棱锥的高)
A
B
C
D
E
O
N
F
考点九.求面面角
6.在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,E是PD的中点,求平面EAC与平面ABCD的夹角.
几何法
公式法
考点十.证明平行垂直
几何法
向量化
公式法
几何法
向量化
