1.4.2用空间向量研究距离夹角问题(第一课时距离) 高中数学人教A版选择性必修1 课件(共31张PPT)
文档属性
| 名称 | 1.4.2用空间向量研究距离夹角问题(第一课时距离) 高中数学人教A版选择性必修1 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 15:41:20 | ||
图片预览







文档简介
(共31张PPT)
1.4.2 用空间向量研究距离、夹角问题
第一课时
如图,在蔬菜大棚基地有一条笔直的公路,某人要在点A处,修建一个蔬菜存储库。如何在公路上选择一个点,修一条公路到达A点,要想使这个路线长度理论上最短,应该如何设计?
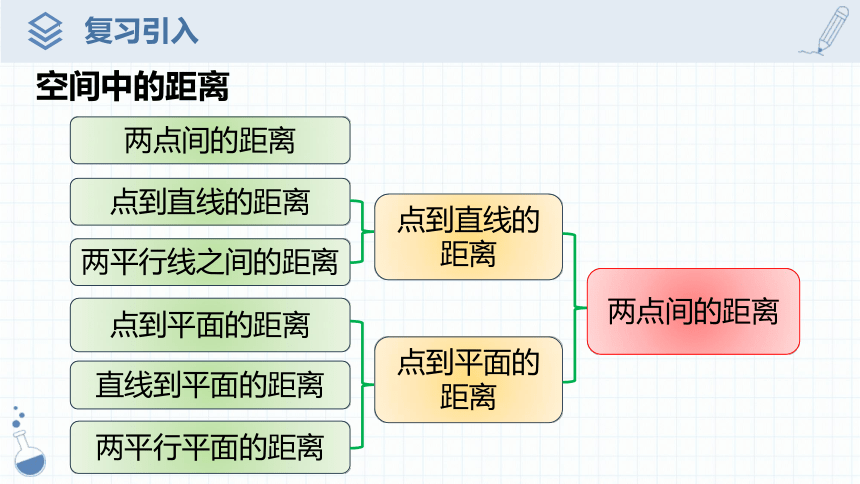
空间中的距离
两点间的距离
点到直线的距离
两平行线之间的距离
点到平面的距离
直线到平面的距离
两平行平面的距离
点到直线的距离
点到平面的距离
两点间的距离
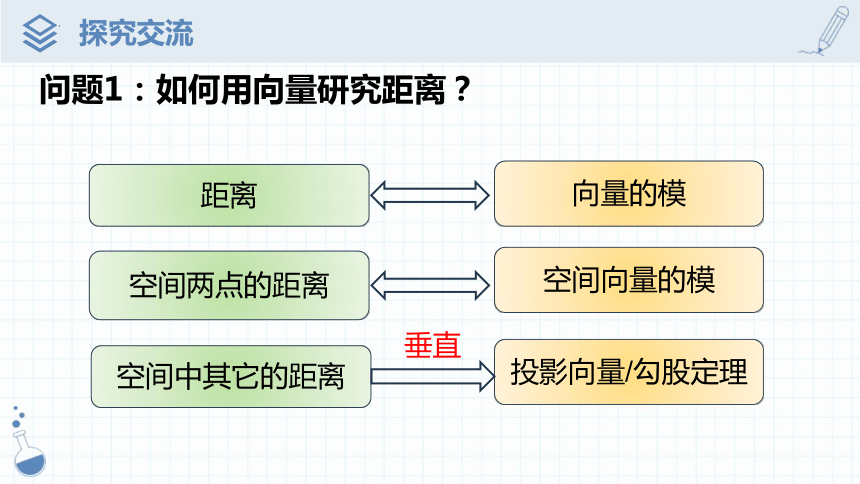
问题1:如何用向量研究距离?
距离
空间两点的距离
空间中其它的距离
向量的模
空间向量的模
投影向量/勾股定理
垂直
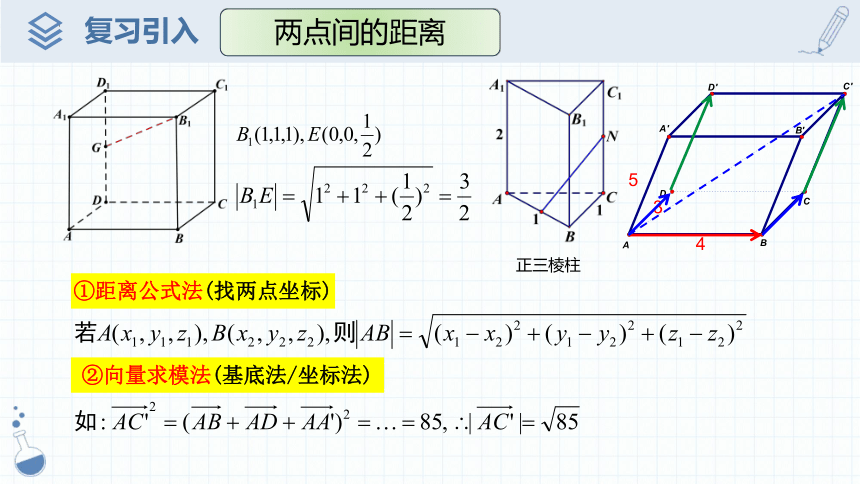
①距离公式法(找两点坐标)
4
3
5
②向量求模法(基底法/坐标法)
正三棱柱
两点间的距离
问题2:如何用向量法求点到直线的距离?
P
Q
A
设是直线的单位方向向量,Q是直线上的垂足
A是直线上的定点
追问1:无法直接计算PQ的情况下可以通过计算哪些方式PQ?
投影向量或者勾股定理
设是直线的单位方向向量,Q是直线上的垂足,A是直线上的定点
追问5:回忆所学初高中知识,求点到直线的距离主要有哪些方法?
【答案】(1)作点到直线的垂线,点到垂足的距离即 为点到直线的距离;
(2)在三角形中用等面积法求解;
(3)向量法,即点到直线的距离为参考向量的平方与投影向量的平方差的算术平方根.
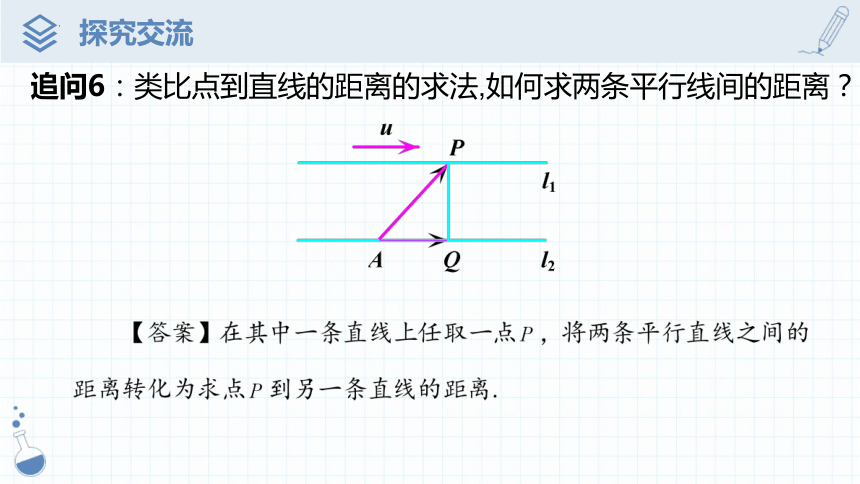
追问6:类比点到直线的距离的求法,如何求两条平行线间的距离?
问题3:类比点到直线的距离的求法,如何求点到平面的距离?
A
P
Q
l
①求
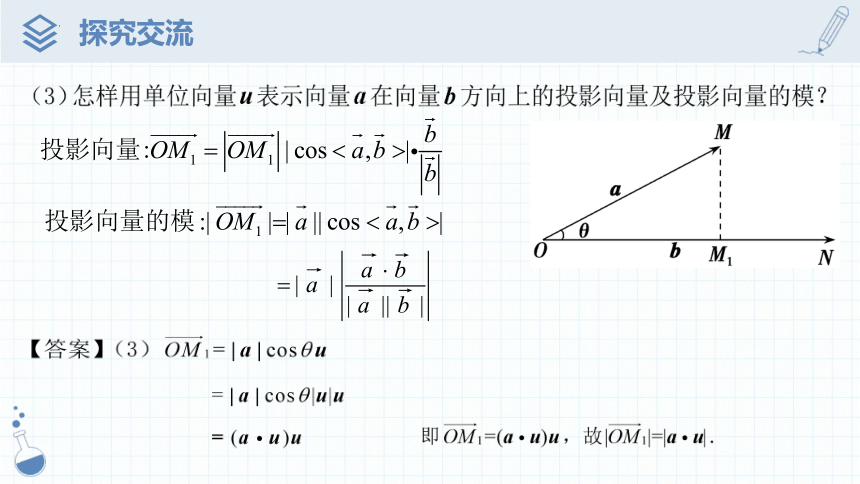
②求在l上的投影向量
③求PQ的长度
A
P
Q
l
追问1:对比点到直线的距离与点到平面的距离公式,有什么联系?
追问3:求点到平面的距离主要有哪些方法?
【答案】 (1)作点到平面的垂线,点到垂足的距离即为 点到平面的距离.
(2)在三棱锥中用等体积法求解.
(3)向量法,点到平面的距离为参考向量与 法向量数量积的绝对值与法向量的模 之比.
例6:如图,在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.(1)求点B到直线AC1的距离;(2)判断直线FC与平面AEC1的位置关系;如果平行,求直线FC 到平面AEC1的距离.
以D1为原点,D1 A1,D1 C1,D1 D所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
例6:如图,在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.(1)求点B到直线AC1的距离;
A(1,0,1),B(1,1,1),C(0,1,1),C1(0,1,0),
E(1,,0),F(1,,1).
问: 相关点的坐标是什么?
问:求哪些向量的坐标?
所以,点B到直线AC1的距离为
等面积法(将点线距离视为三角形的高)
例6:如图,在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.(1)求点B到直线AC1的距离;
问:求哪些向量的坐标?
例6:如图,在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.(2)判断直线FC与平面AEC1的位置关系;如果平行,求直线FC 到平面AEC1的距离.
直线FC//平面AEC1
点F(或C)到平面AEC1的距离
平面的法向量
思考:求两种距离的一般步骤是怎样的?
求点到直线距离的一般步骤:
A
C
B
D
A1
B1
C1
D1
1
1
1
D
C
B
A
A1
B1
C1
D1
F
E
A
C
B
D
A1
B1
C1
D1
E
F
x
y
z
P35-2(1).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1, BB1的中点,求直线A1到直线B1E的距离.
两条平行直线m,l间的距离转化为直线m上任一点到直线l的距离
P35-2(2).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1, BB1的中点,求直线FC1到直线AE的距离.
公式法(求斜线的方向向量在法向量上的投影向量的模)
P35-2(3).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1的中点,求点A1到平面AEB1的距离.
等体积法(将点面距离看作三棱锥的高)
P35-2(3).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1的中点,求点A1到平面AEB1的距离.
A
C
B
D
A1
B1
C1
D1
E
F
x
y
z
P35-2(4).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1, BB1的中点,求直线FC1到平面AB1E的距离.
小结梳理
1.求两点距离
①距离公式法(找两点坐标)
②向量求模法(基底法/坐标法)
2.求点到直线的距离
①公式法(找斜线的方向向量及直线l的方向向量或单位方向向量)
②等面积法(将点线距离视为三角形的高)
3.求直线到直线的距离
先证线线平行m//l,再转化为直线m上任一点到直线l的距离
1.4.2 用空间向量研究距离、夹角问题
第一课时
如图,在蔬菜大棚基地有一条笔直的公路,某人要在点A处,修建一个蔬菜存储库。如何在公路上选择一个点,修一条公路到达A点,要想使这个路线长度理论上最短,应该如何设计?
空间中的距离
两点间的距离
点到直线的距离
两平行线之间的距离
点到平面的距离
直线到平面的距离
两平行平面的距离
点到直线的距离
点到平面的距离
两点间的距离
问题1:如何用向量研究距离?
距离
空间两点的距离
空间中其它的距离
向量的模
空间向量的模
投影向量/勾股定理
垂直
①距离公式法(找两点坐标)
4
3
5
②向量求模法(基底法/坐标法)
正三棱柱
两点间的距离
问题2:如何用向量法求点到直线的距离?
P
Q
A
设是直线的单位方向向量,Q是直线上的垂足
A是直线上的定点
追问1:无法直接计算PQ的情况下可以通过计算哪些方式PQ?
投影向量或者勾股定理
设是直线的单位方向向量,Q是直线上的垂足,A是直线上的定点
追问5:回忆所学初高中知识,求点到直线的距离主要有哪些方法?
【答案】(1)作点到直线的垂线,点到垂足的距离即 为点到直线的距离;
(2)在三角形中用等面积法求解;
(3)向量法,即点到直线的距离为参考向量的平方与投影向量的平方差的算术平方根.
追问6:类比点到直线的距离的求法,如何求两条平行线间的距离?
问题3:类比点到直线的距离的求法,如何求点到平面的距离?
A
P
Q
l
①求
②求在l上的投影向量
③求PQ的长度
A
P
Q
l
追问1:对比点到直线的距离与点到平面的距离公式,有什么联系?
追问3:求点到平面的距离主要有哪些方法?
【答案】 (1)作点到平面的垂线,点到垂足的距离即为 点到平面的距离.
(2)在三棱锥中用等体积法求解.
(3)向量法,点到平面的距离为参考向量与 法向量数量积的绝对值与法向量的模 之比.
例6:如图,在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.(1)求点B到直线AC1的距离;(2)判断直线FC与平面AEC1的位置关系;如果平行,求直线FC 到平面AEC1的距离.
以D1为原点,D1 A1,D1 C1,D1 D所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
例6:如图,在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.(1)求点B到直线AC1的距离;
A(1,0,1),B(1,1,1),C(0,1,1),C1(0,1,0),
E(1,,0),F(1,,1).
问: 相关点的坐标是什么?
问:求哪些向量的坐标?
所以,点B到直线AC1的距离为
等面积法(将点线距离视为三角形的高)
例6:如图,在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.(1)求点B到直线AC1的距离;
问:求哪些向量的坐标?
例6:如图,在棱长为1的正方体ABCD -A1B1C1D1 中,E为线段A1B1的中点,F为线段AB的中点.(2)判断直线FC与平面AEC1的位置关系;如果平行,求直线FC 到平面AEC1的距离.
直线FC//平面AEC1
点F(或C)到平面AEC1的距离
平面的法向量
思考:求两种距离的一般步骤是怎样的?
求点到直线距离的一般步骤:
A
C
B
D
A1
B1
C1
D1
1
1
1
D
C
B
A
A1
B1
C1
D1
F
E
A
C
B
D
A1
B1
C1
D1
E
F
x
y
z
P35-2(1).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1, BB1的中点,求直线A1到直线B1E的距离.
两条平行直线m,l间的距离转化为直线m上任一点到直线l的距离
P35-2(2).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1, BB1的中点,求直线FC1到直线AE的距离.
公式法(求斜线的方向向量在法向量上的投影向量的模)
P35-2(3).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1的中点,求点A1到平面AEB1的距离.
等体积法(将点面距离看作三棱锥的高)
P35-2(3).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1的中点,求点A1到平面AEB1的距离.
A
C
B
D
A1
B1
C1
D1
E
F
x
y
z
P35-2(4).棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是线段DD1, BB1的中点,求直线FC1到平面AB1E的距离.
小结梳理
1.求两点距离
①距离公式法(找两点坐标)
②向量求模法(基底法/坐标法)
2.求点到直线的距离
①公式法(找斜线的方向向量及直线l的方向向量或单位方向向量)
②等面积法(将点线距离视为三角形的高)
3.求直线到直线的距离
先证线线平行m//l,再转化为直线m上任一点到直线l的距离
