人教A版(2019)高数 必修第一册 5.3诱导公式(一)学案
文档属性
| 名称 | 人教A版(2019)高数 必修第一册 5.3诱导公式(一)学案 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 09:39:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.3诱导公式(一)
班级 姓名
学习目标
1.了解公式二、公式三和公式四的推导方法.
2.能够准确记忆公式二、公式三和公式四.
3.掌握公式二、公式三和公式四,并能灵活应用.
学习过程
自学指导 自学检测及课堂展示
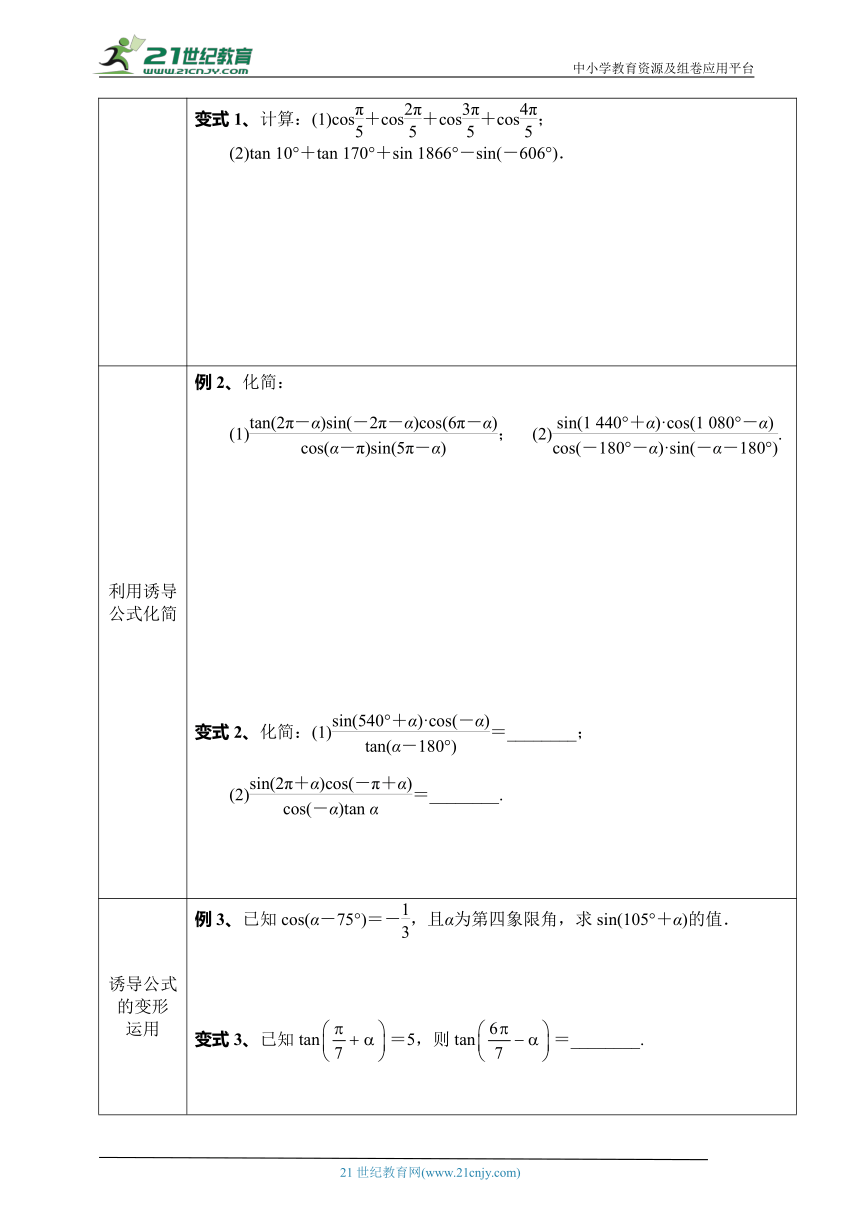
阅读教材,完成右边的内容 终边关系图示公式公式二角π+α与角α的终边关于 对称sin(π+α)= ,cos(π+α)= ,tan(π+α)= .公式三角-α与角α的终边关于 对称sin(-α)= ,cos(-α)= ,tan(-α)= .公式四角π-α与角α的终边关于 对称sin(π-α)= ,cos(π-α)= ,tan(π-α)= .【即时训练】(1)已知sin(θ+180°)<0,cos(θ-180°)>0,则θ是( )A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角(2)(多选题)下列各式运算正确的是( )A.sin(α+180°)=-sin α B.cos(-α+β)=-cos(α-β)C.sin(-α-360°)=-sin α D.cos(-α-β)=cos(α+β)
利用诱导公式求值 例1、利用公式求下列三角函数值:(1)cos 225°; (2)sin; (3)sin; (4)tan(-2040°).变式1、计算:(1)cos+cos+cos+cos; (2)tan 10°+tan 170°+sin 1866°-sin(-606°).
利用诱导公式化简 例2、化简:(1); (2).变式2、化简:(1)=________;(2)=________.
诱导公式的变形运用 例3、已知cos(α-75°)=-,且α为第四象限角,求sin(105°+α)的值.变式3、已知tan=5,则tan=________.
课后作业
一、基础训练题
1.如图所示,角θ的终边与单位圆交于点P,则cos(π-θ)的值为( )
A.- B.- C. D.
2.已知sin(π+α)=,且α是第四象限角,那么cos(α-π)的值是( )
A. B.- C.± D.
3.在△ABC中,cos(A+B)的值等于( )
A.cos C B.-cos C C.sin C D.-sin C
4.(多选)已知角α和β的终边关于x轴对称,则下列各式中正确的是( )
A.sin α=sin β B.sin(α-2π)=-sin β
C.cos α=cos β D.cos(2π-α)=-cos β
5.已知600°角的终边上有一点P(a,-3),则a的值为( )
A. B.-
C. D.-
6.设sin 160°=a,则cos 340°的值是( )
A.1-a2 B.
C.- D.±
7.已知sin=,则sin的值为( )
A. B.-
C. D.-
8.求值:(1)sin=________;(2)cos=________;(3)tan=________.
9.的值等于________.
10.已知sin(α+π)=,且sin αcos α<0,求的值.
11.已知f(α)=.
(1)化简f(α);
(2)若α是第三象限角,且sin(α-π)=,求f(α)的值;
(3)若α=-,求f(α)的值.
二、综合训练题
12.记cos(-80°)=k,则tan 100°等于( )
A. B.-
C. D.-
13.(多选题)已知A=+(k∈Z),则A的值是( )
A.-1 B.-2
C.1 D.2
三、能力提升题
14.设f(x)=asin(πx+α)+bcos(πx+β)+7,α,β均为实数,若f(2020)=8,则f(2021)的值为________.
15.已知f(x)=则f +f 的值为________.
5.3诱导公式(一)
参考答案
1、【答案】C
【解析】由题意可知cos θ=-,cos(π-θ)=-cos θ=-=.故选C.]
【答案】B
【解析】因为sin(π+α)=-sin α=,所以sin α=-.
又α是第四象限角,所以cos α=,所以cos(α-π)=cos(π-α)=-cos α=-.
【答案】B
【解析】∵在△ABC中,A+B=π-C,∴cos(A+B)=cos(π-C)=-cos C.
4、【答案】BC
【解析】由题意可知α=-β,∴sin α=sin(-β)=-sin β;sin(α-2π)=sin α=-sin β;
cos α=cos(-β)=cos β;cos(2π-α)=cos(-α)=cos α=cos β,故选BC.
5、【答案】B
【解析】由题意得tan 600°=-,
又因为tan 600°=tan(360°+240°)=tan 240°=tan(180°+60°)=tan 60°=,
所以-=,所以a=-.
6、【答案】B
【解析】因为sin 160°=a,所以sin(180°-20°)=sin 20°=a,
而cos 340°=cos(360°-20°)=cos 20°=.
7、【答案】C
【解析】sin=sin=-sin=sin=.]
8、【答案】(1) (2)- (3)-
【解析】(1)sin=sin=sin=.
(2)cos=cos=cos=-cos=-.
(3)tan=tan=tan=tan=-tan=-.
9、【答案】-2
【解析】原式==
===-2.
10、[解] 因为sin(α+π)=-sin α=,且sin αcos α<0,
所以sin α=-,cos α=,tan α=-,
所以===-.
11、[解] (1)f(α)=-=-cos α.
(2)∵sin(α-π)=-sin α=,∴sin α=-.
又α是第三象限角,∴cos α=-,∴f(α)=.
(3)∵-=-6×2π+,∴f =-cos=-cos=-cos=-.
12、【答案】B
【解析】∵cos(-80°)=cos 80°=k,sin 80°==,
∴tan 100°=-tan 80°=-.
13、【答案】BD
【解析】当k为偶数时,A=+=2;当k为奇数时,A=-=-2.
14、【答案】6
【解析】因为f(2 020)=asin(2 020π+α)+bcos(2 020π+β)+7=asin α+bcos β+7,
所以asin α+bcos β+7=8,所以asin α+bcos β=1,
又f(2 021)=asin(2 021π+α)+bcos(2 021 π+β)+7=-asin α-bcos β+7=-1+7=6.
所以f(2 021)=6.
15、【答案】-2
【解析】f =sin=sin=sin=,
f =f -1=f -1=f -2=f -2
=sin-2=-sin-2=--2=-,
所以f +f =-=-2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.3诱导公式(一)
班级 姓名
学习目标
1.了解公式二、公式三和公式四的推导方法.
2.能够准确记忆公式二、公式三和公式四.
3.掌握公式二、公式三和公式四,并能灵活应用.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 终边关系图示公式公式二角π+α与角α的终边关于 对称sin(π+α)= ,cos(π+α)= ,tan(π+α)= .公式三角-α与角α的终边关于 对称sin(-α)= ,cos(-α)= ,tan(-α)= .公式四角π-α与角α的终边关于 对称sin(π-α)= ,cos(π-α)= ,tan(π-α)= .【即时训练】(1)已知sin(θ+180°)<0,cos(θ-180°)>0,则θ是( )A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角(2)(多选题)下列各式运算正确的是( )A.sin(α+180°)=-sin α B.cos(-α+β)=-cos(α-β)C.sin(-α-360°)=-sin α D.cos(-α-β)=cos(α+β)
利用诱导公式求值 例1、利用公式求下列三角函数值:(1)cos 225°; (2)sin; (3)sin; (4)tan(-2040°).变式1、计算:(1)cos+cos+cos+cos; (2)tan 10°+tan 170°+sin 1866°-sin(-606°).
利用诱导公式化简 例2、化简:(1); (2).变式2、化简:(1)=________;(2)=________.
诱导公式的变形运用 例3、已知cos(α-75°)=-,且α为第四象限角,求sin(105°+α)的值.变式3、已知tan=5,则tan=________.
课后作业
一、基础训练题
1.如图所示,角θ的终边与单位圆交于点P,则cos(π-θ)的值为( )
A.- B.- C. D.
2.已知sin(π+α)=,且α是第四象限角,那么cos(α-π)的值是( )
A. B.- C.± D.
3.在△ABC中,cos(A+B)的值等于( )
A.cos C B.-cos C C.sin C D.-sin C
4.(多选)已知角α和β的终边关于x轴对称,则下列各式中正确的是( )
A.sin α=sin β B.sin(α-2π)=-sin β
C.cos α=cos β D.cos(2π-α)=-cos β
5.已知600°角的终边上有一点P(a,-3),则a的值为( )
A. B.-
C. D.-
6.设sin 160°=a,则cos 340°的值是( )
A.1-a2 B.
C.- D.±
7.已知sin=,则sin的值为( )
A. B.-
C. D.-
8.求值:(1)sin=________;(2)cos=________;(3)tan=________.
9.的值等于________.
10.已知sin(α+π)=,且sin αcos α<0,求的值.
11.已知f(α)=.
(1)化简f(α);
(2)若α是第三象限角,且sin(α-π)=,求f(α)的值;
(3)若α=-,求f(α)的值.
二、综合训练题
12.记cos(-80°)=k,则tan 100°等于( )
A. B.-
C. D.-
13.(多选题)已知A=+(k∈Z),则A的值是( )
A.-1 B.-2
C.1 D.2
三、能力提升题
14.设f(x)=asin(πx+α)+bcos(πx+β)+7,α,β均为实数,若f(2020)=8,则f(2021)的值为________.
15.已知f(x)=则f +f 的值为________.
5.3诱导公式(一)
参考答案
1、【答案】C
【解析】由题意可知cos θ=-,cos(π-θ)=-cos θ=-=.故选C.]
【答案】B
【解析】因为sin(π+α)=-sin α=,所以sin α=-.
又α是第四象限角,所以cos α=,所以cos(α-π)=cos(π-α)=-cos α=-.
【答案】B
【解析】∵在△ABC中,A+B=π-C,∴cos(A+B)=cos(π-C)=-cos C.
4、【答案】BC
【解析】由题意可知α=-β,∴sin α=sin(-β)=-sin β;sin(α-2π)=sin α=-sin β;
cos α=cos(-β)=cos β;cos(2π-α)=cos(-α)=cos α=cos β,故选BC.
5、【答案】B
【解析】由题意得tan 600°=-,
又因为tan 600°=tan(360°+240°)=tan 240°=tan(180°+60°)=tan 60°=,
所以-=,所以a=-.
6、【答案】B
【解析】因为sin 160°=a,所以sin(180°-20°)=sin 20°=a,
而cos 340°=cos(360°-20°)=cos 20°=.
7、【答案】C
【解析】sin=sin=-sin=sin=.]
8、【答案】(1) (2)- (3)-
【解析】(1)sin=sin=sin=.
(2)cos=cos=cos=-cos=-.
(3)tan=tan=tan=tan=-tan=-.
9、【答案】-2
【解析】原式==
===-2.
10、[解] 因为sin(α+π)=-sin α=,且sin αcos α<0,
所以sin α=-,cos α=,tan α=-,
所以===-.
11、[解] (1)f(α)=-=-cos α.
(2)∵sin(α-π)=-sin α=,∴sin α=-.
又α是第三象限角,∴cos α=-,∴f(α)=.
(3)∵-=-6×2π+,∴f =-cos=-cos=-cos=-.
12、【答案】B
【解析】∵cos(-80°)=cos 80°=k,sin 80°==,
∴tan 100°=-tan 80°=-.
13、【答案】BD
【解析】当k为偶数时,A=+=2;当k为奇数时,A=-=-2.
14、【答案】6
【解析】因为f(2 020)=asin(2 020π+α)+bcos(2 020π+β)+7=asin α+bcos β+7,
所以asin α+bcos β+7=8,所以asin α+bcos β=1,
又f(2 021)=asin(2 021π+α)+bcos(2 021 π+β)+7=-asin α-bcos β+7=-1+7=6.
所以f(2 021)=6.
15、【答案】-2
【解析】f =sin=sin=sin=,
f =f -1=f -1=f -2=f -2
=sin-2=-sin-2=--2=-,
所以f +f =-=-2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
