人教A版(2019)高数 必修第一册 5.4三角函数的图象与性质综合应用 学案
文档属性
| 名称 | 人教A版(2019)高数 必修第一册 5.4三角函数的图象与性质综合应用 学案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 09:46:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.4三角函数的图象与性质综合应用
班级 姓名
学习目标
1.理解正弦函数、余弦函数、正切函数的定义及其图象与性质;
2.掌握求解函数周期性、单调性、对称性与最值的方法.
学习过程
自学指导 自学检测及课堂展示
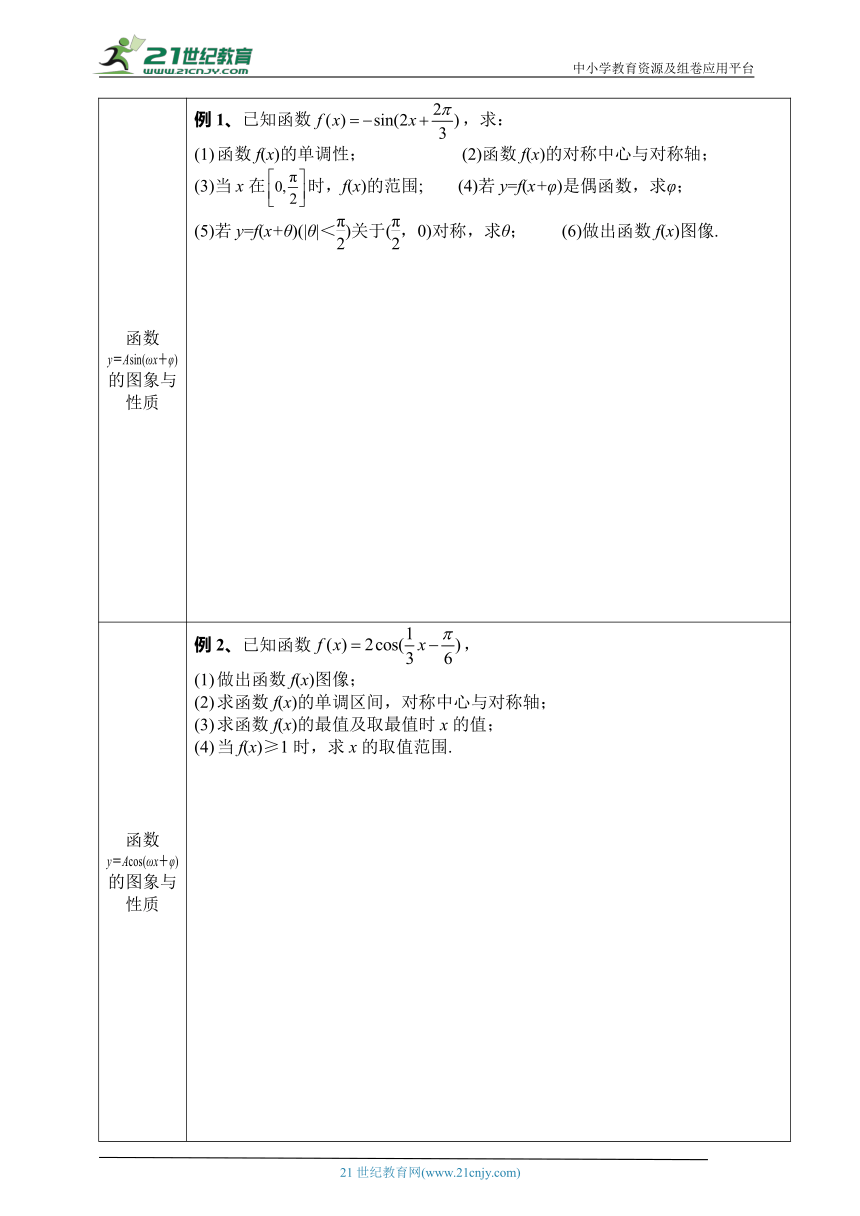
完成右边的内容 1.正弦函数、余弦函数、正切函数的图象与性质函数y=sin xy=cos xy=tan x图象定义域值域单调性奇偶性对称性周期性2.函数y=Asin(ωx+φ)(A>0,ω>0)的性质周期性y=Asin(ωx+φ)存在周期性,其最小正周期为T=奇偶性φ=kπ(k∈Z)时,函数y=Asin(ωx+φ)为奇函数;φ=kπ+(k∈Z)时,函数y=Asin(ωx+φ)为偶函数单调性根据y=sin t和t=ωx+φ的单调性来研究,由-+2kπ≤ωx+φ≤+2kπ,k∈Z得单调递增区间;由+2kπ≤ωx+φ≤+2kπ,k∈Z得单调递减区间对称性利用y=sin x的对称中心为(kπ,0)(k∈Z)求解,令ωx+φ=kπ(k∈Z),求得x. 利用y=sin x的对称轴为x=kπ+(k∈Z)求解,令ωx+φ=kπ+(k∈Z),求得其对称轴
函数y=Asin(ωx+φ)的图象与性质 已知函数,求:函数f(x)的单调性; (2)函数f(x)的对称中心与对称轴; (3)当x在时,f(x)的范围; (4)若y=f(x+φ)是偶函数,求φ; (5)若y=f(x+θ)(|θ|<)关于(,0)对称,求θ; (6)做出函数f(x)图像.
函数y=Acos(ωx+φ)的图象与性质 已知函数,做出函数f(x)图像; 求函数f(x)的单调区间,对称中心与对称轴;求函数f(x)的最值及取最值时x的值; 当f(x)≥1时,求x的取值范围.
函数y=Atan(ωx+φ)的图象与性质 已知,求:f(x)的定义域; (2)f(x)的单调区间; (3)f(x)的对称轴;(4)当f(x)<1时,求x的取值范围.
换元法的运用 例4、(1)函数y=cos2x+sin x的最大值为________.(2)当x∈时,函数y=3-sin x-2cos2x的值域为________.
课后作业
一、基础训练题
1.下列函数中,在区间上恒正且是增函数的是( )
A.y=sin x B.y=cos x C.y=-sin x D.y=-cos x
2.设函数f(x)=2sin,若对任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为( )
A.4 B.2 C.1 D.
3.(多选题)设函数f(x)=cos(x+),则下列结论正确的是( )
A.f(x)的一个周期为-2π B.y=f(x)的图象关于直线x=对称
C.f(x+π)的一个零点为x= D.f(x)在(,π)上单调递减
4.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为4π,且 x∈R,有f(x)≤f()成立,则f(x)图象的一个对称中心坐标是( )
A.(-,0) B.(-,0) C.(,0) D.(,0)
5.(多选题)下列关于函数y=tan的说法正确的是( )
A.在区间上单调递增 B.最小正周期是π
C.图象关于成中心对称 D.图象关于直线x=成轴对称
6.(多选题)已知函数f(x)=2sin+1,则下列说法中正确的是( )
A.函数f(x)的图象关于点对称 B.函数f(x)图象的一条对称轴是x=-
C.若x∈,则函数f(x)的最小值为+1 D.若07.若函数f(x)=sin ωx(ω>0)在区间上单调递增,在区间上单调递减,则ω=________.
8.已知函数f(x)=sin(2x+φ)(-π<φ<0)图象的一条对称轴是直线x=,则φ的值为__________.
9.已知函数f(x)=sin.
(1)求函数f(x)的单调递增区间;
(2)当x∈时,求函数f(x)的最大值和最小值.
二、综合训练题
10.定义在R上的函数f(x)既是偶函数,又是周期函数,若f(x)的最小正周期为π,且当x∈时,f(x)=sin x,则f 等于( )
A.- B. C.- D.
11.已知f(x)是定义在(-3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,那么不等式f(x)cos x<0的解集是__________.
12.求函数y=cos2x-sin x,x∈的最值.
三、能力提升题
13.已知函数f(x)=asin+b(a>0).当x∈时,f(x)的最大值为,最小值是
-2,求a和b的值.
5.4三角函数的图象与性质
参考答案
1、【答案】D
【解析】作出四个函数的图象(图略),知y=sin x,y=cos x在上单调递减,不符合;
而y=-sin x的图象虽满足在上单调递增但其值为负,所以只有D符合,故选D.
2、【答案】B
【解析】依题意得f(x1)是f(x)的最小值,f(x2)是f(x)的最大值.因此|x1-x2|=T(k∈Z).
∴当k=0时,|x1-x2|min=T=×=2.
3、【答案】ABC
【解析】A项,因为f(x)=cos(x+)的周期为2kπ(k∈Z),所以f(x)的一个周期为-2π,A项正确;
B项,因为f(x)=cos(x+)图象的对称轴为直线x=kπ-(k∈Z),所以y=f(x)的图象关于直线x=对称,B项正确;
C项,f(x+π)=cos(x+).令x+=kπ+(k∈Z),得x=kπ-,当k=1时,x=,
所以f(x+π)的一个零点为x=,C项正确;
D项,因为f(x)=cos(x+)的单调递减区间为[2kπ-,2kπ+](k∈Z),
单调递增区间为[2kπ+,2kπ+](k∈Z),
所以(,)是f(x)的单调递减区间,[,π)是f(x)的单调递增区间,D项错误.]
4、【答案】A
【解析】由f(x)=sin(ωx+φ)的最小正周期为4π,得ω=.
因为f(x)≤f()恒成立,所以f(x)max=f(),即×+φ=+2kπ(k∈Z),
由|φ|<,得φ=,故f(x)=sin(x+).令x+=kπ(k∈Z),得x=2kπ-(k∈Z),
故f(x)图象的对称中心为(2kπ-,0)(k∈Z),当k=0时,f(x)图象的对称中心为(-,0).
5、【答案】AB
【解析】令kπ-6、【答案】BC
【解析】对于函数f(x)=2sin+1,
当x=时,f(x)=+1,故选项A错误;当x=-时,f(x)=-1,为最小值,故函数f(x)图象的一条对称轴是x=-,故选项B正确;当x∈,2x-∈,故当2x-=或时,f(x)取得最小值为+1,故选项C正确;若07、【答案】
【解析】由已知得=,∴T=,∴ω==.
8、【答案】-π
【解析】由题意知2×+φ=+kπ,k∈Z,所以φ=+kπ,k∈Z,又-π<φ<0,所以φ=-π.
9.解 (1)令2kπ-≤2x+≤2kπ+,k∈Z,则kπ-≤x≤kπ+,k∈Z.
故函数f(x)的单调递增区间为,k∈Z.
(2)因为当x∈时,≤2x+≤,所以-1≤sin≤,所以-≤f(x)≤1,
所以当x∈时,函数f(x)的最大值为1,最小值为-.
10、【答案】D
【解析】 f =f =f =f =f =f =sin=.
11、【答案】∪(0,1)∪
【解析】∵f(x)是(-3,3)上的奇函数,∴g(x)=f(x)·cos x是(-3,3)上的奇函数,
从而观察图象(略)可知所求不等式的解集为∪(0,1)∪.
12、[解] y=cos2x-sin x=1-sin2x-sin x=-2+.
因为-≤x≤,-≤sin x≤,
所以当sin x=-,即x=-时,函数取得最大值,ymax=;
当sin x=,即x=时,函数取得最小值,ymin=-.
13、[解] ∵0≤x≤,∴-≤2x-≤,∴-≤sin≤1,
∴f(x)max=a+b=,f(x)min=-a+b=-2.
由得
21世纪教育网 www.21cn5.4三角函数的图象与性质
班级 姓名
学习目标
1.理解正弦函数、余弦函数、正切函数的定义及其图象与性质;
2.掌握求解函数周期性、单调性、对称性与最值的方法.
学习过程
自学指导 自学检测及课堂展示
完成右边的内容 1.正弦函数、余弦函数、正切函数的图象与性质函数y=sin xy=cos xy=tan x图象定义域值域单调性奇偶性对称性周期性2.函数y=Asin(ωx+φ)(A>0,ω>0)的性质周期性y=Asin(ωx+φ)存在周期性,其最小正周期为T=eq \f(2π,ω)奇偶性φ=kπ(k∈Z)时,函数y=Asin(ωx+φ)为奇函数;φ=kπ+eq \f(π,2)(k∈Z)时,函数y=Asin(ωx+φ)为偶函数单调性根据y=sin t和t=ωx+φ的单调性来研究,由-eq \f(π,2)+2kπ≤ωx+φ≤eq \f(π,2)+2kπ,k∈Z得单调递增区间;由eq \f(π,2)+2kπ≤ωx+φ≤eq \f(3π,2)+2kπ,k∈Z得单调递减区间对称性利用y=sin x的对称中心为(kπ,0)(k∈Z)求解,令ωx+φ=kπ(k∈Z),求得x. 利用y=sin x的对称轴为x=kπ+eq \f(π,2)(k∈Z)求解,令ωx+φ=kπ+eq \f(π,2)(k∈Z),求得其对称轴
函数y=Asin(ωx+φ)的图象与性质 已知函数,求:函数f(x)的单调性; (2)函数f(x)的对称中心与对称轴; (3)当x在时,f(x)的范围; (4)若y=f(x+φ)是偶函数,求φ; (5)若y=f(x+θ)(|θ|<eq \f(π,2))关于(eq \f(π,2),0)对称,求θ; (6)做出函数f(x)图像.
函数y=Acos(ωx+φ)的图象与性质 已知函数,做出函数f(x)图像; 求函数f(x)的单调区间,对称中心与对称轴;求函数f(x)的最值及取最值时x的值; 当f(x)≥1时,求x的取值范围.
函数y=Atan(ωx+φ)的图象与性质 已知,求:f(x)的定义域; (2)f(x)的单调区间; (3)f(x)的对称轴;(4)当f(x)<1时,求x的取值范围.
换元法的运用 例4、(1)函数y=cos2x+sin x的最大值为________.(2)当x∈时,函数y=3-sin x-2cos2x的值域为________.
课后作业
一、基础训练题
1.下列函数中,在区间上恒正且是增函数的是( )
A.y=sin x B.y=cos x C.y=-sin x D.y=-cos x
2.设函数f(x)=2sin,若对任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为( )
A.4 B.2 C.1 D.eq \f(1,2)
3.(多选题)设函数f(x)=cos(x+eq \f(π,3)),则下列结论正确的是( )
A.f(x)的一个周期为-2π B.y=f(x)的图象关于直线x=eq \f(8π,3)对称
C.f(x+π)的一个零点为x=eq \f(π,6) D.f(x)在(eq \f(π,2),π)上单调递减
4.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<eq \f(π,2))的最小正周期为4π,且 x∈R,有f(x)≤f(eq \f(π,3))成立,则f(x)图象的一个对称中心坐标是( )
A.(-eq \f(2π,3),0) B.(-eq \f(π,3),0) C.(eq \f(2π,3),0) D.(eq \f(5π,3),0)
5.(多选题)下列关于函数y=tan的说法正确的是( )
A.在区间上单调递增 B.最小正周期是π
C.图象关于成中心对称 D.图象关于直线x=eq \f(π,6)成轴对称
6.(多选题)已知函数f(x)=2sin+1,则下列说法中正确的是( )
A.函数f(x)的图象关于点对称 B.函数f(x)图象的一条对称轴是x=-eq \f(π,12)
C.若x∈,则函数f(x)的最小值为+1 D.若07.若函数f(x)=sin ωx(ω>0)在区间上单调递增,在区间上单调递减,则ω=________.
8.已知函数f(x)=sin(2x+φ)(-π<φ<0)图象的一条对称轴是直线x=eq \f(π,6),则φ的值为__________.
9.已知函数f(x)=sin.
(1)求函数f(x)的单调递增区间;
(2)当x∈时,求函数f(x)的最大值和最小值.
二、综合训练题
10.定义在R上的函数f(x)既是偶函数,又是周期函数,若f(x)的最小正周期为π,且当x∈时,f(x)=sin x,则f 等于( )
A.-eq \f(1,2) B.eq \f(1,2) C.- D.
11.已知f(x)是定义在(-3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,那么不等式f(x)cos x<0的解集是__________.
12.求函数y=cos2x-sin x,x∈的最值.
三、能力提升题
13.已知函数f(x)=asin+b(a>0).当x∈时,f(x)的最大值为,最小值是
-2,求a和b的值.
5.4三角函数的图象与性质
参考答案
1、【答案】D
【解析】作出四个函数的图象(图略),知y=sin x,y=cos x在eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(π,2),π))上单调递减,不符合;
而y=-sin x的图象虽满足在eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(π,2),π))上单调递增但其值为负,所以只有D符合,故选D.
2、【答案】B
【解析】依题意得f(x1)是f(x)的最小值,f(x2)是f(x)的最大值.因此|x1-x2|=eq \b\lc\(\rc\)(\a\vs4\al\co1(k+\f(1,2)))T(k∈Z).
∴当k=0时,|x1-x2|min=eq \f(1,2)T=eq \f(1,2)×eq \f(2π,\f(π,2))=2.
3、【答案】ABC
【解析】A项,因为f(x)=cos(x+eq \f(π,3))的周期为2kπ(k∈Z),所以f(x)的一个周期为-2π,A项正确;
B项,因为f(x)=cos(x+eq \f(π,3))图象的对称轴为直线x=kπ-eq \f(π,3)(k∈Z),所以y=f(x)的图象关于直线x=eq \f(8π,3)对称,B项正确;
C项,f(x+π)=cos(x+eq \f(4π,3)).令x+eq \f(4π,3)=kπ+eq \f(π,2)(k∈Z),得x=kπ-eq \f(5π,6),当k=1时,x=eq \f(π,6),
所以f(x+π)的一个零点为x=eq \f(π,6),C项正确;
D项,因为f(x)=cos(x+eq \f(π,3))的单调递减区间为[2kπ-eq \f(π,3),2kπ+eq \f(2π,3)](k∈Z),
单调递增区间为[2kπ+eq \f(2π,3),2kπ+eq \f(5π,3)](k∈Z),
所以(eq \f(π,2),eq \f(2π,3))是f(x)的单调递减区间,[eq \f(2π,3),π)是f(x)的单调递增区间,D项错误.]
4、【答案】A
【解析】由f(x)=sin(ωx+φ)的最小正周期为4π,得ω=eq \f(1,2).
因为f(x)≤f(eq \f(π,3))恒成立,所以f(x)max=f(eq \f(π,3)),即eq \f(1,2)×eq \f(π,3)+φ=eq \f(π,2)+2kπ(k∈Z),
由|φ|<eq \f(π,2),得φ=eq \f(π,3),故f(x)=sin(eq \f(1,2)x+eq \f(π,3)).令eq \f(1,2)x+eq \f(π,3)=kπ(k∈Z),得x=2kπ-eq \f(2π,3)(k∈Z),
故f(x)图象的对称中心为(2kπ-eq \f(2π,3),0)(k∈Z),当k=0时,f(x)图象的对称中心为(-eq \f(2π,3),0).
5、【答案】AB
【解析】令kπ-eq \f(π,2)6、【答案】BC
【解析】对于函数f(x)=2sineq \b\lc\(\rc\)(\a\vs4\al\co1(2x-\f(π,3)))+1,
当x=eq \f(π,3)时,f(x)=eq \r(3)+1,故选项A错误;当x=-eq \f(π,12)时,f(x)=-1,为最小值,故函数f(x)图象的一条对称轴是x=-eq \f(π,12),故选项B正确;当x∈eq \b\lc\[\rc\](\a\vs4\al\co1(\f(π,3),\f(π,2))),2x-eq \f(π,3)∈eq \b\lc\[\rc\](\a\vs4\al\co1(\f(π,3),\f(2π,3))),故当2x-eq \f(π,3)=eq \f(π,3)或eq \f(2π,3)时,f(x)取得最小值为eq \r(3)+1,故选项C正确;若07、【答案】eq \f(3,2)
【解析】由已知得eq \f(T,4)=eq \f(π,3),∴T=eq \f(4π,3),∴ω=eq \f(2π,T)=eq \f(3,2).
8、【答案】-eq \f(5,6)π
【解析】由题意知2×eq \f(π,6)+φ=eq \f(π,2)+kπ,k∈Z,所以φ=eq \f(π,6)+kπ,k∈Z,又-π<φ<0,所以φ=-eq \f(5,6)π.
9.解 (1)令2kπ-eq \f(π,2)≤2x+eq \f(π,4)≤2kπ+eq \f(π,2),k∈Z,则kπ-eq \f(3π,8)≤x≤kπ+eq \f(π,8),k∈Z.
故函数f(x)的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\co1(kπ-\f(3π,8),kπ+\f(π,8))),k∈Z.
(2)因为当x∈eq \b\lc\[\rc\](\a\vs4\al\co1(\f(π,4),\f(3π,4)))时,eq \f(3π,4)≤2x+eq \f(π,4)≤eq \f(7π,4),所以-1≤sineq \b\lc\(\rc\)(\a\vs4\al\co1(2x+\f(π,4)))≤eq \f(\r(2),2),所以-eq \r(2)≤f(x)≤1,
所以当x∈eq \b\lc\[\rc\](\a\vs4\al\co1(\f(π,4),\f(3π,4)))时,函数f(x)的最大值为1,最小值为-eq \r(2).
10、【答案】D
【解析】 f eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(5π,3)))=f eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(5π,3)-π))=f eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(2π,3)))=f eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(2π,3)-π))=f eq \b\lc\(\rc\)(\a\vs4\al\co1(-\f(π,3)))=f eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(π,3)))=sineq \f(π,3)=eq \f(\r(3),2).
11、【答案】eq \b\lc\(\rc\)(\a\vs4\al\co1(-\f(π,2),-1))∪(0,1)∪eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(π,2),3))
【解析】∵f(x)是(-3,3)上的奇函数,∴g(x)=f(x)·cos x是(-3,3)上的奇函数,
从而观察图象(略)可知所求不等式的解集为eq \b\lc\(\rc\)(\a\vs4\al\co1(-\f(π,2),-1))∪(0,1)∪eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(π,2),3)).
12、[解] y=cos2x-sin x=1-sin2x-sin x=-eq \b\lc\(\rc\)(\a\vs4\al\co1(sin x+\f(1,2)))2+eq \f(5,4).
因为-eq \f(π,4)≤x≤eq \f(π,4),-eq \f(\r(2),2)≤sin x≤eq \f(\r(2),2),
所以当sin x=-eq \f(1,2),即x=-eq \f(π,6)时,函数取得最大值,ymax=eq \f(5,4);
当sin x=eq \f(\r(2),2),即x=eq \f(π,4)时,函数取得最小值,ymin=eq \f(1,2)-eq \f(\r(2),2).
13、[解] ∵0≤x≤eq \f(π,2),∴-eq \f(π,3)≤2x-eq \f(π,3)≤eq \f(2π,3),∴-eq \f(\r(3),2)≤sineq \b\lc\(\rc\)(\a\vs4\al\co1(2x-\f(π,3)))≤1,
∴f(x)max=a+b=eq \r(3),f(x)min=-eq \f(\r(3),2)a+b=-2.
由eq \b\lc\{\rc\ (\a\vs4\al\co1(a+b=\r(3),,-\f(\r(3),2)a+b=-2,))得eq \b\lc\{\rc\ (\a\vs4\al\co1(a=2,,b=-2+\r(3).))
jy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.4三角函数的图象与性质综合应用
班级 姓名
学习目标
1.理解正弦函数、余弦函数、正切函数的定义及其图象与性质;
2.掌握求解函数周期性、单调性、对称性与最值的方法.
学习过程
自学指导 自学检测及课堂展示
完成右边的内容 1.正弦函数、余弦函数、正切函数的图象与性质函数y=sin xy=cos xy=tan x图象定义域值域单调性奇偶性对称性周期性2.函数y=Asin(ωx+φ)(A>0,ω>0)的性质周期性y=Asin(ωx+φ)存在周期性,其最小正周期为T=奇偶性φ=kπ(k∈Z)时,函数y=Asin(ωx+φ)为奇函数;φ=kπ+(k∈Z)时,函数y=Asin(ωx+φ)为偶函数单调性根据y=sin t和t=ωx+φ的单调性来研究,由-+2kπ≤ωx+φ≤+2kπ,k∈Z得单调递增区间;由+2kπ≤ωx+φ≤+2kπ,k∈Z得单调递减区间对称性利用y=sin x的对称中心为(kπ,0)(k∈Z)求解,令ωx+φ=kπ(k∈Z),求得x. 利用y=sin x的对称轴为x=kπ+(k∈Z)求解,令ωx+φ=kπ+(k∈Z),求得其对称轴
函数y=Asin(ωx+φ)的图象与性质 已知函数,求:函数f(x)的单调性; (2)函数f(x)的对称中心与对称轴; (3)当x在时,f(x)的范围; (4)若y=f(x+φ)是偶函数,求φ; (5)若y=f(x+θ)(|θ|<)关于(,0)对称,求θ; (6)做出函数f(x)图像.
函数y=Acos(ωx+φ)的图象与性质 已知函数,做出函数f(x)图像; 求函数f(x)的单调区间,对称中心与对称轴;求函数f(x)的最值及取最值时x的值; 当f(x)≥1时,求x的取值范围.
函数y=Atan(ωx+φ)的图象与性质 已知,求:f(x)的定义域; (2)f(x)的单调区间; (3)f(x)的对称轴;(4)当f(x)<1时,求x的取值范围.
换元法的运用 例4、(1)函数y=cos2x+sin x的最大值为________.(2)当x∈时,函数y=3-sin x-2cos2x的值域为________.
课后作业
一、基础训练题
1.下列函数中,在区间上恒正且是增函数的是( )
A.y=sin x B.y=cos x C.y=-sin x D.y=-cos x
2.设函数f(x)=2sin,若对任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为( )
A.4 B.2 C.1 D.
3.(多选题)设函数f(x)=cos(x+),则下列结论正确的是( )
A.f(x)的一个周期为-2π B.y=f(x)的图象关于直线x=对称
C.f(x+π)的一个零点为x= D.f(x)在(,π)上单调递减
4.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为4π,且 x∈R,有f(x)≤f()成立,则f(x)图象的一个对称中心坐标是( )
A.(-,0) B.(-,0) C.(,0) D.(,0)
5.(多选题)下列关于函数y=tan的说法正确的是( )
A.在区间上单调递增 B.最小正周期是π
C.图象关于成中心对称 D.图象关于直线x=成轴对称
6.(多选题)已知函数f(x)=2sin+1,则下列说法中正确的是( )
A.函数f(x)的图象关于点对称 B.函数f(x)图象的一条对称轴是x=-
C.若x∈,则函数f(x)的最小值为+1 D.若0
8.已知函数f(x)=sin(2x+φ)(-π<φ<0)图象的一条对称轴是直线x=,则φ的值为__________.
9.已知函数f(x)=sin.
(1)求函数f(x)的单调递增区间;
(2)当x∈时,求函数f(x)的最大值和最小值.
二、综合训练题
10.定义在R上的函数f(x)既是偶函数,又是周期函数,若f(x)的最小正周期为π,且当x∈时,f(x)=sin x,则f 等于( )
A.- B. C.- D.
11.已知f(x)是定义在(-3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,那么不等式f(x)cos x<0的解集是__________.
12.求函数y=cos2x-sin x,x∈的最值.
三、能力提升题
13.已知函数f(x)=asin+b(a>0).当x∈时,f(x)的最大值为,最小值是
-2,求a和b的值.
5.4三角函数的图象与性质
参考答案
1、【答案】D
【解析】作出四个函数的图象(图略),知y=sin x,y=cos x在上单调递减,不符合;
而y=-sin x的图象虽满足在上单调递增但其值为负,所以只有D符合,故选D.
2、【答案】B
【解析】依题意得f(x1)是f(x)的最小值,f(x2)是f(x)的最大值.因此|x1-x2|=T(k∈Z).
∴当k=0时,|x1-x2|min=T=×=2.
3、【答案】ABC
【解析】A项,因为f(x)=cos(x+)的周期为2kπ(k∈Z),所以f(x)的一个周期为-2π,A项正确;
B项,因为f(x)=cos(x+)图象的对称轴为直线x=kπ-(k∈Z),所以y=f(x)的图象关于直线x=对称,B项正确;
C项,f(x+π)=cos(x+).令x+=kπ+(k∈Z),得x=kπ-,当k=1时,x=,
所以f(x+π)的一个零点为x=,C项正确;
D项,因为f(x)=cos(x+)的单调递减区间为[2kπ-,2kπ+](k∈Z),
单调递增区间为[2kπ+,2kπ+](k∈Z),
所以(,)是f(x)的单调递减区间,[,π)是f(x)的单调递增区间,D项错误.]
4、【答案】A
【解析】由f(x)=sin(ωx+φ)的最小正周期为4π,得ω=.
因为f(x)≤f()恒成立,所以f(x)max=f(),即×+φ=+2kπ(k∈Z),
由|φ|<,得φ=,故f(x)=sin(x+).令x+=kπ(k∈Z),得x=2kπ-(k∈Z),
故f(x)图象的对称中心为(2kπ-,0)(k∈Z),当k=0时,f(x)图象的对称中心为(-,0).
5、【答案】AB
【解析】令kπ-
【解析】对于函数f(x)=2sin+1,
当x=时,f(x)=+1,故选项A错误;当x=-时,f(x)=-1,为最小值,故函数f(x)图象的一条对称轴是x=-,故选项B正确;当x∈,2x-∈,故当2x-=或时,f(x)取得最小值为+1,故选项C正确;若0
【解析】由已知得=,∴T=,∴ω==.
8、【答案】-π
【解析】由题意知2×+φ=+kπ,k∈Z,所以φ=+kπ,k∈Z,又-π<φ<0,所以φ=-π.
9.解 (1)令2kπ-≤2x+≤2kπ+,k∈Z,则kπ-≤x≤kπ+,k∈Z.
故函数f(x)的单调递增区间为,k∈Z.
(2)因为当x∈时,≤2x+≤,所以-1≤sin≤,所以-≤f(x)≤1,
所以当x∈时,函数f(x)的最大值为1,最小值为-.
10、【答案】D
【解析】 f =f =f =f =f =f =sin=.
11、【答案】∪(0,1)∪
【解析】∵f(x)是(-3,3)上的奇函数,∴g(x)=f(x)·cos x是(-3,3)上的奇函数,
从而观察图象(略)可知所求不等式的解集为∪(0,1)∪.
12、[解] y=cos2x-sin x=1-sin2x-sin x=-2+.
因为-≤x≤,-≤sin x≤,
所以当sin x=-,即x=-时,函数取得最大值,ymax=;
当sin x=,即x=时,函数取得最小值,ymin=-.
13、[解] ∵0≤x≤,∴-≤2x-≤,∴-≤sin≤1,
∴f(x)max=a+b=,f(x)min=-a+b=-2.
由得
21世纪教育网 www.21cn5.4三角函数的图象与性质
班级 姓名
学习目标
1.理解正弦函数、余弦函数、正切函数的定义及其图象与性质;
2.掌握求解函数周期性、单调性、对称性与最值的方法.
学习过程
自学指导 自学检测及课堂展示
完成右边的内容 1.正弦函数、余弦函数、正切函数的图象与性质函数y=sin xy=cos xy=tan x图象定义域值域单调性奇偶性对称性周期性2.函数y=Asin(ωx+φ)(A>0,ω>0)的性质周期性y=Asin(ωx+φ)存在周期性,其最小正周期为T=eq \f(2π,ω)奇偶性φ=kπ(k∈Z)时,函数y=Asin(ωx+φ)为奇函数;φ=kπ+eq \f(π,2)(k∈Z)时,函数y=Asin(ωx+φ)为偶函数单调性根据y=sin t和t=ωx+φ的单调性来研究,由-eq \f(π,2)+2kπ≤ωx+φ≤eq \f(π,2)+2kπ,k∈Z得单调递增区间;由eq \f(π,2)+2kπ≤ωx+φ≤eq \f(3π,2)+2kπ,k∈Z得单调递减区间对称性利用y=sin x的对称中心为(kπ,0)(k∈Z)求解,令ωx+φ=kπ(k∈Z),求得x. 利用y=sin x的对称轴为x=kπ+eq \f(π,2)(k∈Z)求解,令ωx+φ=kπ+eq \f(π,2)(k∈Z),求得其对称轴
函数y=Asin(ωx+φ)的图象与性质 已知函数,求:函数f(x)的单调性; (2)函数f(x)的对称中心与对称轴; (3)当x在时,f(x)的范围; (4)若y=f(x+φ)是偶函数,求φ; (5)若y=f(x+θ)(|θ|<eq \f(π,2))关于(eq \f(π,2),0)对称,求θ; (6)做出函数f(x)图像.
函数y=Acos(ωx+φ)的图象与性质 已知函数,做出函数f(x)图像; 求函数f(x)的单调区间,对称中心与对称轴;求函数f(x)的最值及取最值时x的值; 当f(x)≥1时,求x的取值范围.
函数y=Atan(ωx+φ)的图象与性质 已知,求:f(x)的定义域; (2)f(x)的单调区间; (3)f(x)的对称轴;(4)当f(x)<1时,求x的取值范围.
换元法的运用 例4、(1)函数y=cos2x+sin x的最大值为________.(2)当x∈时,函数y=3-sin x-2cos2x的值域为________.
课后作业
一、基础训练题
1.下列函数中,在区间上恒正且是增函数的是( )
A.y=sin x B.y=cos x C.y=-sin x D.y=-cos x
2.设函数f(x)=2sin,若对任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为( )
A.4 B.2 C.1 D.eq \f(1,2)
3.(多选题)设函数f(x)=cos(x+eq \f(π,3)),则下列结论正确的是( )
A.f(x)的一个周期为-2π B.y=f(x)的图象关于直线x=eq \f(8π,3)对称
C.f(x+π)的一个零点为x=eq \f(π,6) D.f(x)在(eq \f(π,2),π)上单调递减
4.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<eq \f(π,2))的最小正周期为4π,且 x∈R,有f(x)≤f(eq \f(π,3))成立,则f(x)图象的一个对称中心坐标是( )
A.(-eq \f(2π,3),0) B.(-eq \f(π,3),0) C.(eq \f(2π,3),0) D.(eq \f(5π,3),0)
5.(多选题)下列关于函数y=tan的说法正确的是( )
A.在区间上单调递增 B.最小正周期是π
C.图象关于成中心对称 D.图象关于直线x=eq \f(π,6)成轴对称
6.(多选题)已知函数f(x)=2sin+1,则下列说法中正确的是( )
A.函数f(x)的图象关于点对称 B.函数f(x)图象的一条对称轴是x=-eq \f(π,12)
C.若x∈,则函数f(x)的最小值为+1 D.若0
8.已知函数f(x)=sin(2x+φ)(-π<φ<0)图象的一条对称轴是直线x=eq \f(π,6),则φ的值为__________.
9.已知函数f(x)=sin.
(1)求函数f(x)的单调递增区间;
(2)当x∈时,求函数f(x)的最大值和最小值.
二、综合训练题
10.定义在R上的函数f(x)既是偶函数,又是周期函数,若f(x)的最小正周期为π,且当x∈时,f(x)=sin x,则f 等于( )
A.-eq \f(1,2) B.eq \f(1,2) C.- D.
11.已知f(x)是定义在(-3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,那么不等式f(x)cos x<0的解集是__________.
12.求函数y=cos2x-sin x,x∈的最值.
三、能力提升题
13.已知函数f(x)=asin+b(a>0).当x∈时,f(x)的最大值为,最小值是
-2,求a和b的值.
5.4三角函数的图象与性质
参考答案
1、【答案】D
【解析】作出四个函数的图象(图略),知y=sin x,y=cos x在eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(π,2),π))上单调递减,不符合;
而y=-sin x的图象虽满足在eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(π,2),π))上单调递增但其值为负,所以只有D符合,故选D.
2、【答案】B
【解析】依题意得f(x1)是f(x)的最小值,f(x2)是f(x)的最大值.因此|x1-x2|=eq \b\lc\(\rc\)(\a\vs4\al\co1(k+\f(1,2)))T(k∈Z).
∴当k=0时,|x1-x2|min=eq \f(1,2)T=eq \f(1,2)×eq \f(2π,\f(π,2))=2.
3、【答案】ABC
【解析】A项,因为f(x)=cos(x+eq \f(π,3))的周期为2kπ(k∈Z),所以f(x)的一个周期为-2π,A项正确;
B项,因为f(x)=cos(x+eq \f(π,3))图象的对称轴为直线x=kπ-eq \f(π,3)(k∈Z),所以y=f(x)的图象关于直线x=eq \f(8π,3)对称,B项正确;
C项,f(x+π)=cos(x+eq \f(4π,3)).令x+eq \f(4π,3)=kπ+eq \f(π,2)(k∈Z),得x=kπ-eq \f(5π,6),当k=1时,x=eq \f(π,6),
所以f(x+π)的一个零点为x=eq \f(π,6),C项正确;
D项,因为f(x)=cos(x+eq \f(π,3))的单调递减区间为[2kπ-eq \f(π,3),2kπ+eq \f(2π,3)](k∈Z),
单调递增区间为[2kπ+eq \f(2π,3),2kπ+eq \f(5π,3)](k∈Z),
所以(eq \f(π,2),eq \f(2π,3))是f(x)的单调递减区间,[eq \f(2π,3),π)是f(x)的单调递增区间,D项错误.]
4、【答案】A
【解析】由f(x)=sin(ωx+φ)的最小正周期为4π,得ω=eq \f(1,2).
因为f(x)≤f(eq \f(π,3))恒成立,所以f(x)max=f(eq \f(π,3)),即eq \f(1,2)×eq \f(π,3)+φ=eq \f(π,2)+2kπ(k∈Z),
由|φ|<eq \f(π,2),得φ=eq \f(π,3),故f(x)=sin(eq \f(1,2)x+eq \f(π,3)).令eq \f(1,2)x+eq \f(π,3)=kπ(k∈Z),得x=2kπ-eq \f(2π,3)(k∈Z),
故f(x)图象的对称中心为(2kπ-eq \f(2π,3),0)(k∈Z),当k=0时,f(x)图象的对称中心为(-eq \f(2π,3),0).
5、【答案】AB
【解析】令kπ-eq \f(π,2)
【解析】对于函数f(x)=2sineq \b\lc\(\rc\)(\a\vs4\al\co1(2x-\f(π,3)))+1,
当x=eq \f(π,3)时,f(x)=eq \r(3)+1,故选项A错误;当x=-eq \f(π,12)时,f(x)=-1,为最小值,故函数f(x)图象的一条对称轴是x=-eq \f(π,12),故选项B正确;当x∈eq \b\lc\[\rc\](\a\vs4\al\co1(\f(π,3),\f(π,2))),2x-eq \f(π,3)∈eq \b\lc\[\rc\](\a\vs4\al\co1(\f(π,3),\f(2π,3))),故当2x-eq \f(π,3)=eq \f(π,3)或eq \f(2π,3)时,f(x)取得最小值为eq \r(3)+1,故选项C正确;若0
【解析】由已知得eq \f(T,4)=eq \f(π,3),∴T=eq \f(4π,3),∴ω=eq \f(2π,T)=eq \f(3,2).
8、【答案】-eq \f(5,6)π
【解析】由题意知2×eq \f(π,6)+φ=eq \f(π,2)+kπ,k∈Z,所以φ=eq \f(π,6)+kπ,k∈Z,又-π<φ<0,所以φ=-eq \f(5,6)π.
9.解 (1)令2kπ-eq \f(π,2)≤2x+eq \f(π,4)≤2kπ+eq \f(π,2),k∈Z,则kπ-eq \f(3π,8)≤x≤kπ+eq \f(π,8),k∈Z.
故函数f(x)的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\co1(kπ-\f(3π,8),kπ+\f(π,8))),k∈Z.
(2)因为当x∈eq \b\lc\[\rc\](\a\vs4\al\co1(\f(π,4),\f(3π,4)))时,eq \f(3π,4)≤2x+eq \f(π,4)≤eq \f(7π,4),所以-1≤sineq \b\lc\(\rc\)(\a\vs4\al\co1(2x+\f(π,4)))≤eq \f(\r(2),2),所以-eq \r(2)≤f(x)≤1,
所以当x∈eq \b\lc\[\rc\](\a\vs4\al\co1(\f(π,4),\f(3π,4)))时,函数f(x)的最大值为1,最小值为-eq \r(2).
10、【答案】D
【解析】 f eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(5π,3)))=f eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(5π,3)-π))=f eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(2π,3)))=f eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(2π,3)-π))=f eq \b\lc\(\rc\)(\a\vs4\al\co1(-\f(π,3)))=f eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(π,3)))=sineq \f(π,3)=eq \f(\r(3),2).
11、【答案】eq \b\lc\(\rc\)(\a\vs4\al\co1(-\f(π,2),-1))∪(0,1)∪eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(π,2),3))
【解析】∵f(x)是(-3,3)上的奇函数,∴g(x)=f(x)·cos x是(-3,3)上的奇函数,
从而观察图象(略)可知所求不等式的解集为eq \b\lc\(\rc\)(\a\vs4\al\co1(-\f(π,2),-1))∪(0,1)∪eq \b\lc\(\rc\)(\a\vs4\al\co1(\f(π,2),3)).
12、[解] y=cos2x-sin x=1-sin2x-sin x=-eq \b\lc\(\rc\)(\a\vs4\al\co1(sin x+\f(1,2)))2+eq \f(5,4).
因为-eq \f(π,4)≤x≤eq \f(π,4),-eq \f(\r(2),2)≤sin x≤eq \f(\r(2),2),
所以当sin x=-eq \f(1,2),即x=-eq \f(π,6)时,函数取得最大值,ymax=eq \f(5,4);
当sin x=eq \f(\r(2),2),即x=eq \f(π,4)时,函数取得最小值,ymin=eq \f(1,2)-eq \f(\r(2),2).
13、[解] ∵0≤x≤eq \f(π,2),∴-eq \f(π,3)≤2x-eq \f(π,3)≤eq \f(2π,3),∴-eq \f(\r(3),2)≤sineq \b\lc\(\rc\)(\a\vs4\al\co1(2x-\f(π,3)))≤1,
∴f(x)max=a+b=eq \r(3),f(x)min=-eq \f(\r(3),2)a+b=-2.
由eq \b\lc\{\rc\ (\a\vs4\al\co1(a+b=\r(3),,-\f(\r(3),2)a+b=-2,))得eq \b\lc\{\rc\ (\a\vs4\al\co1(a=2,,b=-2+\r(3).))
jy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
