冀教版八年级上册第十八章综合检测题

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
冀教版八年级上册第十八章综合检测题A
河北 刘新民
一、认认真真选，沉着应战！
1．在下面的叙述中，能确定物体位置的选项的是( )
①图书大厦在火车站的西北方向 ②上午8点，小红在人民商场一层的东北角等我
③小明家在自强小区14号楼3单元501室 ④体育馆在距人民广场650米的地方
A.①② B.②③ C.①②③ D.②③④
2．如图，表示点的位置，正确的是（ ）
A．距O点3km的地方
B．在O点的东北方向上
C．在O点东偏北的方向
D．在O点北偏东方向，距O点3km的地方
3．已知点M在x轴上，且到y轴的距离是3，则M点的坐标是（ ）
A.（3，0） B.（0，3） C.（3，0）或（－3，0） D.（0，3）或（0，－3）
4．将点P先向左平移2个单位，再向下平移2个单位得点P′，则点P′的坐标为（　　）
A、　　　　B、　　　　　C、　　　　D、
5．在平面直角坐标系中，点P（2x－6,x－5）在第四象限，则x的取值范围是（ ）
A.3＜x＜5 B.－3＜x＜5 C.－5＜x＜3 D.－5＜x＜－3
6．若一元二次方程所对应的直线是，那么下列各点不在直线上的是（ 　）
A．（） 　　B． C． D．
7．四边形ABCD在平面直角坐标系中的位置如图所示，若AB⊥AD，AB∥CD，且AB=5，A点坐标为（－2，7），则B点坐标为（ ）
A.（－2，2） B.（－2，12）
C.（3，7） D.（－7，7）
8．若以一个二元一次方程组中的两个方程画出的直线平行，则此方程组（ ）
A.无解 B.有唯一解　　　　　C.有无数解 D.以上都有可能
9．直角坐标系内的一条线段上的所有点的横坐标都加1，而纵坐标不变，则这条线段被（　　）
Ａ．向左平移一个单位 Ｂ．向右平移一个单位
Ｃ．向上平移一个单位 Ｄ．向下平移一个单位
10．已知点、点（，）、点（，1），以、、三点为顶点画平行四边形，则第四个顶点不可能在( )
Ａ．第一象限　　Ｂ．第二象限　　Ｃ．第三象限　　Ｄ．第四象限
二、仔仔细细填，记录自信！
11．在电影院内，确定一个座位一般需要　　　　　个数据．“7排3号”与“3排7号”的含义　　　　（填“相同”或“不同”）．如果记“10排20号”为，则表示　　　　　　．表示“15排13号”为　　　　　．　
12．如图，如果士所在位置的坐标为（－1,－2），相所在位置的坐标为（2,－2），那么，炮所在位置的坐标为 .
13．将平面直角坐标系中的图形横向拉长2倍，则图形中各点的横坐标_______，纵坐标__________.
14．已知点P1（a－1,5）和P2（2，b－1）关于x轴对称，则（a＋b）2003的值为_____.
15．点P在直线x＋y=0上,并且到x轴的距离等于4,则点P的坐标是____________.
16．在平面直角坐标系中有一个图形，如果将这个图形上所有点的纵坐标都减去5，横坐标不变，则所得图形与原图形的关系是_______________。
17．小明在平面直角坐标系中画一个正方形，其中四个顶点到原点的距离相等，其中一个顶点的坐标为，则在第四象限内的顶点的坐标是　　　　　．
18．在一次中学生野外生存训练活动中，每位队员都配发了一张地
图，并接到训练任务：要求36小时之内到达目的地．但是，地
图上并未标明目的地的具体位置，仅知道两地坐标分别为
，且目的地离两地的距离分别为10、6，
如图所示，则目的地确切位置的坐标为　　　　　　　．
19．若直线2x－y－3=0与直线5x＋2y－a=0相交于点(3,3),则a=____________.
20．如图，A表示三经路与一纬路的十字路口，B表示一经路与三纬路的十字路口，如果用（3，1）→(3,2)→(3,3)→(2,3)→(1,3)表示由A到B的一条路径，用同样的方式写出另外一条由A到B的路径：（3，1）→（____________）→（____________）→（____________）→（1，3）.
三、平心静气做，展示智慧！
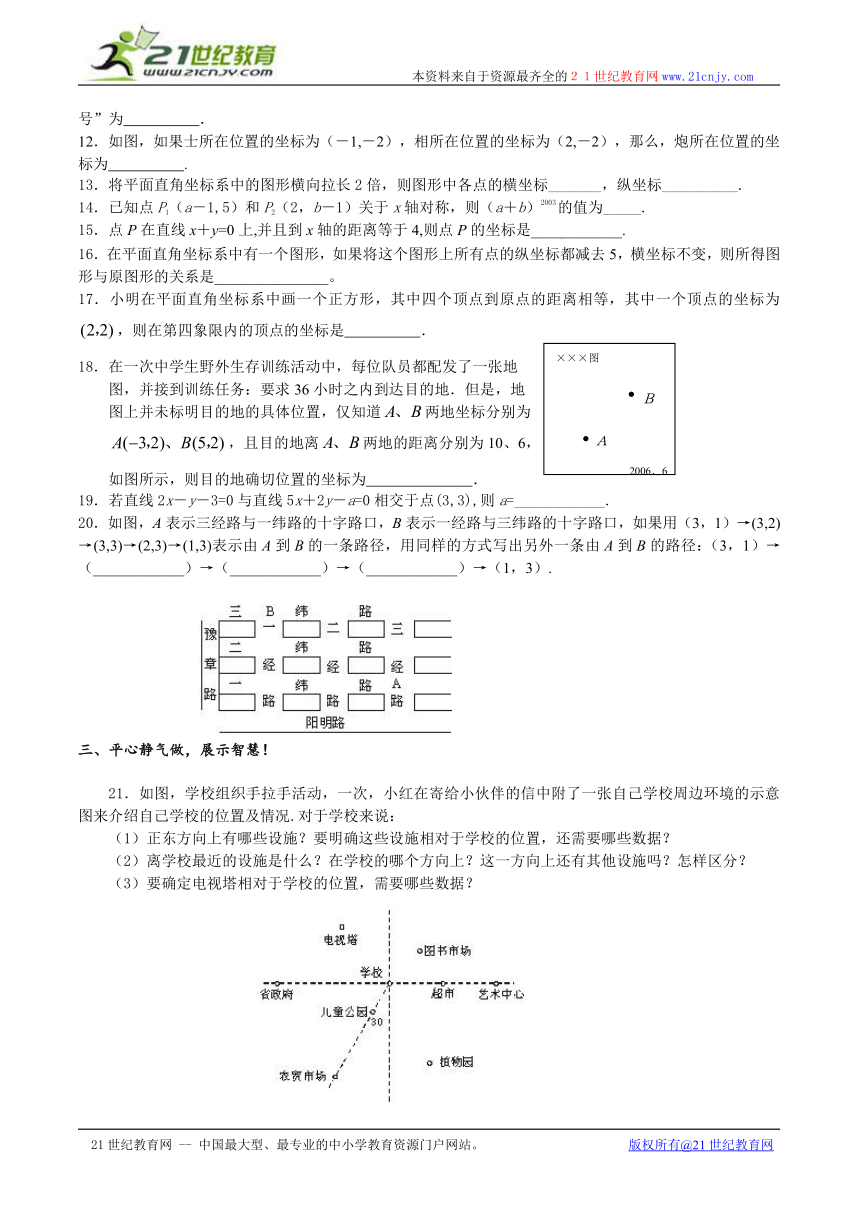
21．如图，学校组织手拉手活动，一次，小红在寄给小伙伴的信中附了一张自己学校周边环境的示意图来介绍自己学校的位置及情况.对于学校来说：
（1）正东方向上有哪些设施？要明确这些设施相对于学校的位置，还需要哪些数据？
（2）离学校最近的设施是什么？在学校的哪个方向上？这一方向上还有其他设施吗？怎样区分？
（3）要确定电视塔相对于学校的位置，需要哪些数据？
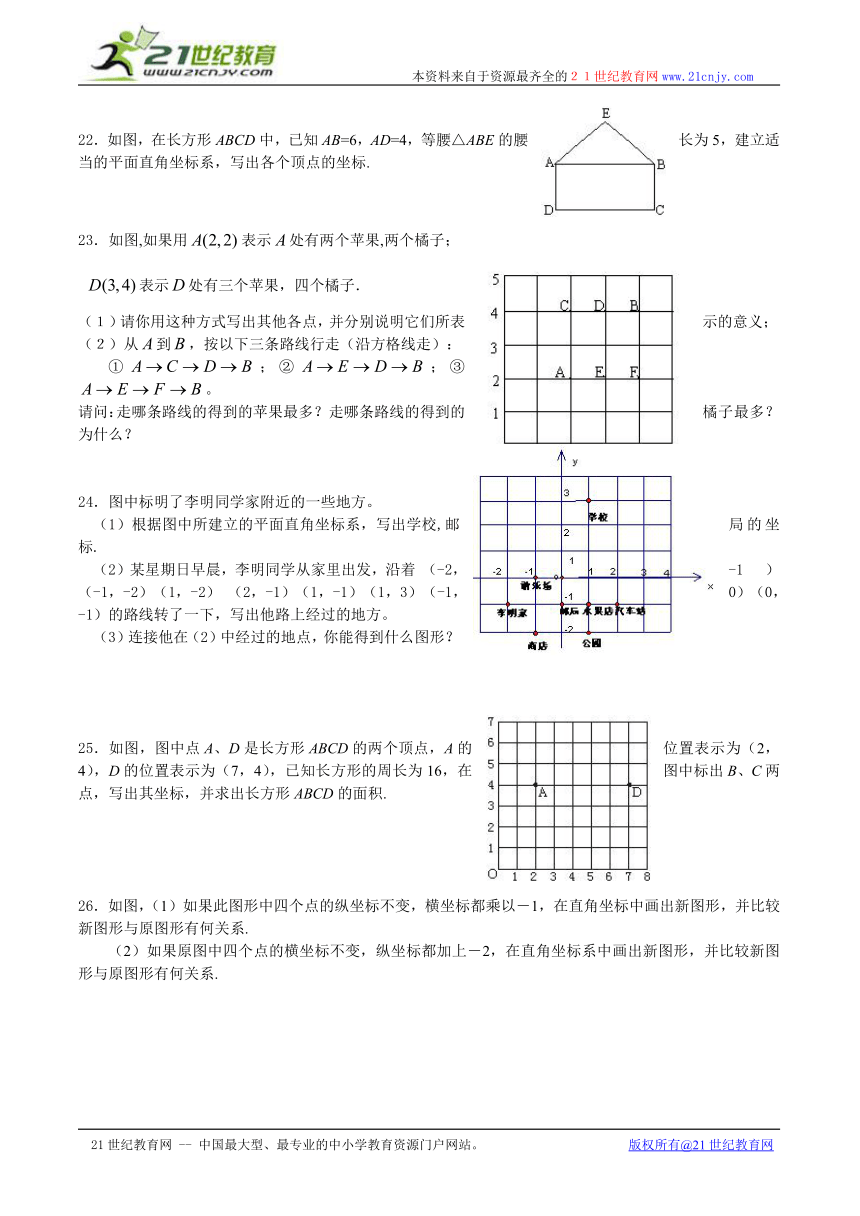
22．如图，在长方形ABCD中，已知AB=6，AD=4，等腰△ABE的腰长为5，建立适当的平面直角坐标系，写出各个顶点的坐标.
23．如图,如果用表示处有两个苹果,两个橘子；
表示处有三个苹果，四个橘子．
（１）请你用这种方式写出其他各点，并分别说明它们所表示的意义；
（２）从到，按以下三条路线行走（沿方格线走）：
①；②；③。
请问：走哪条路线的得到的苹果最多？走哪条路线的得到的橘子最多？为什么？
24．图中标明了李明同学家附近的一些地方。
（1）根据图中所建立的平面直角坐标系，写出学校,邮局的坐标.
（2）某星期日早晨，李明同学从家里出发，沿着 （-2，-1）（-1，-2）（1，-2） （2，-1）（1，-1）（1，3）（-1，0）（0，-1）的路线转了一下，写出他路上经过的地方。
（3）连接他在（2）中经过的地点，你能得到什么图形？
25．如图，图中点A、D是长方形ABCD的两个顶点，A的位置表示为（2，4），D的位置表示为（7，4），已知长方形的周长为16，在图中标出B、C两点，写出其坐标，并求出长方形ABCD的面积.
26．如图，（1）如果此图形中四个点的纵坐标不变，横坐标都乘以－1，在直角坐标中画出新图形，并比较新图形与原图形有何关系.
（2）如果原图中四个点的横坐标不变，纵坐标都加上－2，在直角坐标系中画出新图形，并比较新图形与原图形有何关系.
四、发散思维，游刃有余！
27．我们发现当图形平移时,图形的形状、大小都不变,只是位置变了.但是图形横向、纵向伸缩后,形状和大小都发生了变化,下面我们从面积的变化来感受一下这种变化.
首先在坐标系中画出长方形ABCD,其各点的坐标分别为A(1,2)、B(1,－1)、C(6,－1)、D(6,2),则AB=____________,BC=____________,S长方形ABCD=____________.(如下图
(1)将各点的横坐标不变,纵坐标都乘以2,并把所得各点依次连结,得到长方形A1B1C1D1,A1(1,4),B1(1,－2),C1(6,－2),D1(6,4),则A1B1=________,B1C1=______,
S长方形ABCD=____________.显然S长方形ABCD=2S长方形ABCD,即图形纵向拉长为原来的2倍,面积也变为原来的2倍.
(2)很显然,若将原长方形ABCD纵向缩为原来的,面积也就会变为原来的.横向伸缩(纵向不变)的变化规律与此相同.
(3)探究:若将长方形ABCD各点的横坐标都乘以2,纵坐标都乘以3,则所得长方形的面积是原长方形ABCD面积的____________倍.
(4)若将原长方形ABCD各点的横坐标都乘以m,纵坐标都乘以n(m、n均为正数),则所得长方形的面积是原长方形ABCD面积的____________倍;若m、n中有负数时,面积的变化规律如何
参考答案
一、1—5：BDCBA 6—10：BCABC
二、11．两，不同，20排10号，
12．（－3,1）
13．扩大2倍； 不变
14．－1
15．(－4,4)或(4,－4)
16．是原图形向下平移5个单位得到的
17．
18．或
19．21
20．路径不唯一，如（2，1）→(1,1)→(1,2);(2,1)→(2,2)→(2,3);(3,2)→(2,2)→(1,2)等
三、21．（1）正东方向上有超市和艺术中心.要明确这些设施相对于学校的位置还需要距离.（2）离学校最近的设施是儿童公园，它在学校南偏西30°的方向上；这一方向上还有农贸市场；它们距学校的距离不同.（3）要确定电视塔相对于学校的位置，需要方位角和距离.
22．建立如图所示的坐标系.
在Rt△AOE中，AE=5，AO=3，则OE=4，所以各个顶点的坐标分别为A（－3，0）、B（3，0）、C（3，－4）、D（－3，－4）、E（0，4）.
23．（1）表示处有四个苹果,四个橘子；表示处有两个苹果,四个橘子；
表示处有三个苹果,两个橘子；表示处有四个苹果,两个橘子。
（2）：得到的苹果数为：2+2+3+4=11（个），得到的橘子数为：2+4+4+4=14（个）；
：得到的苹果数为：2+3+3+4=12（个），得到的橘子数为：2+2+4+4=12（个）；
：得到的苹果数为：2+3+4+4=13（个），得到的橘子数为：2+2+2+4=10（个）；
所以走得到的苹果最多，走得到的橘子最多。
24．（1）学校（1，3）， 邮局（0，-1）；
（2）商店、公园、汽车站、水果店、学校、娱乐场、邮局；（3）一只小船。
25．B（2，1）或(2,7)，C（7，1）或(7,7)，由AD长为5，周长为16可知，长为5，宽为3，则S=15.
26．（1）四个点的坐标变化为（0，0）、（－6，3）、（－4，0）、（－6，－3），如图所示.新图形与原图形关于y轴对称.
（2）四个点的坐标变化为（0，－2）、（6，1）、（4，－2）、（6，－5），如图所示.新图形是由原图形向下平移2个单位长度得到的.
四、27．3 5 15 (1)6 5 30 (3)6 (4)mn
当m、n中出现负数时,会引起图形关于坐标轴或轴对称的变换,但图形的形状、大小与m、n的绝对值有关,所以面积是原长方形ABCD面积的|mn|倍.
×××图
2006．6
Ｂ
Ａ
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网