4.1几何图形(第2课时)课件(共38张PPT)2023-2024学年七年级数学上册(人教版)
文档属性
| 名称 | 4.1几何图形(第2课时)课件(共38张PPT)2023-2024学年七年级数学上册(人教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 00:00:00 | ||
图片预览






文档简介
(共38张PPT)
第四章 几何图形初步
4.1 几何图形
4.1.2 从不同的方向看立体图形和立体图形的展开图
学习目标
1、了解立体图形与平面图形之间的联系;
2、能画出简单立体图形从不同方向看得到的平面图形;
3、了解研究立体图形的方法,体会一个立体图形按照不同方式展开可得到不同的平面展开图;
4、通过展开与折叠,了解棱柱、棱锥、圆柱、圆锥、长方体、正方体的表面展开图或根据展开图判断立体图形;
情景引入
想一想:这是为什么呢?
从不同方向看山可看到“峰”,看到“岭”,那么从不同方向看几何体又能看到什么呢?你想知道吗?
现在就让我们一起来学习今天的“从三个方向看物体的形状”.
漫画“6”与“9”
思考:为什么他们会对同一个物体产生不同的看法?
知识点一 从不同方向看几何体
知识精讲
A
B
D
C
每台摄像机拍到的分别是下面的哪张照片?
B
A
C
D
当我们从不同的方向观察同一物体时,通常可以看到不同的图形.
知识精讲
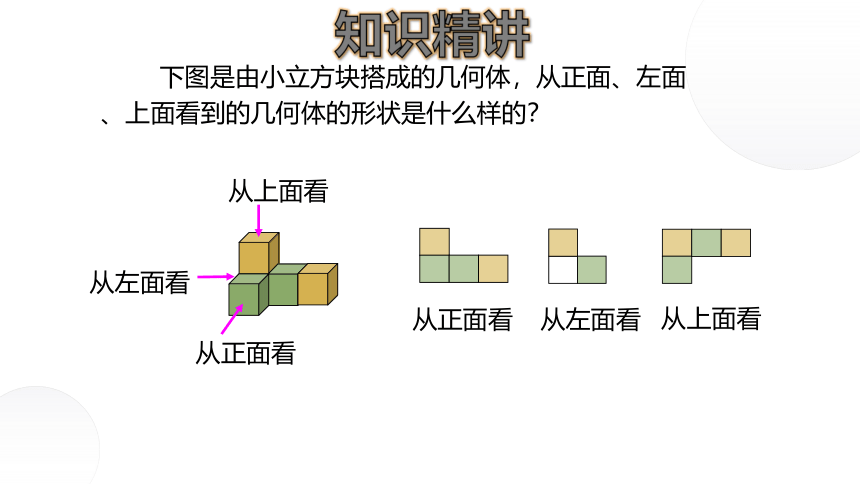
下图是由小立方块搭成的几何体,从正面、左面、上面看到的几何体的形状是什么样的?
从左面看
从正面看
从左面看
从上面看
从正面看
从上面看
知识精讲
视图来自于投影.投影现象广泛存在于我们日常生活中,根据光源发出的光线不同,有中心投影和平行投影,如:灯光的光线可以看作是从一点发出的,我们称这种投影为中心投影;太阳的光线可以看是平行的,我们称这种投影为平行投影;视图是一种特殊的平行投影.
中心投影
平行投影
知识精讲
正面
侧面
水平面
主视图
俯视图
左视图
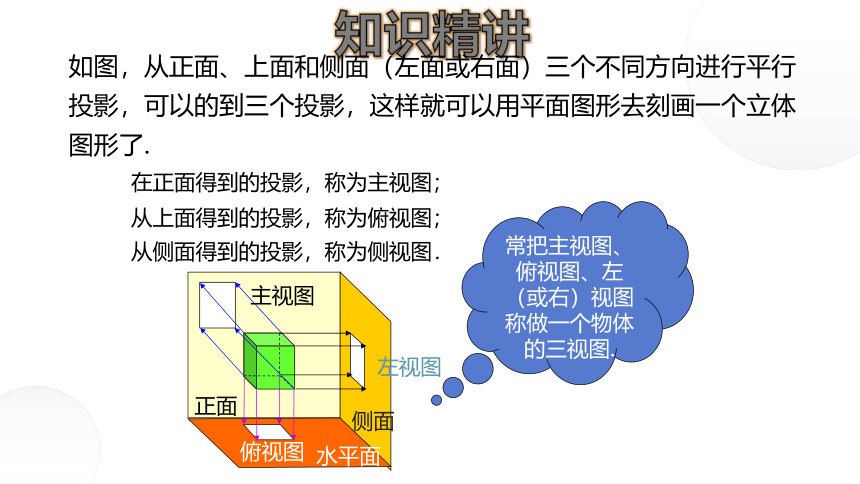
如图,从正面、上面和侧面(左面或右面)三个不同方向进行平行投影,可以的到三个投影,这样就可以用平面图形去刻画一个立体图形了.
从上面得到的投影,称为俯视图;
从侧面得到的投影,称为侧视图.
在正面得到的投影,称为主视图;
常把主视图、俯视图、左(或右)视图称做一个物体的三视图.
知识精讲
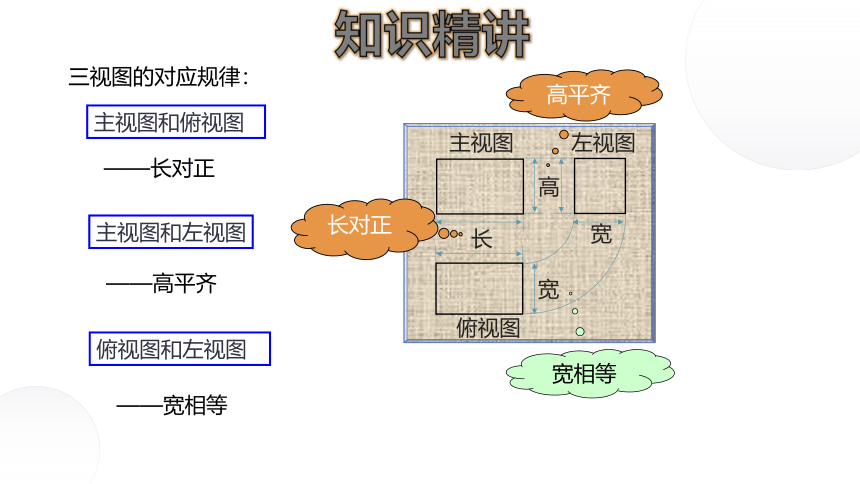
三视图的对应规律:
俯视图和左视图
主视图和俯视图
主视图和左视图
——长对正
——高平齐
——宽相等
主视图
俯视图
左视图
高
长
宽
宽
高平齐
长对正
宽相等
知识精讲
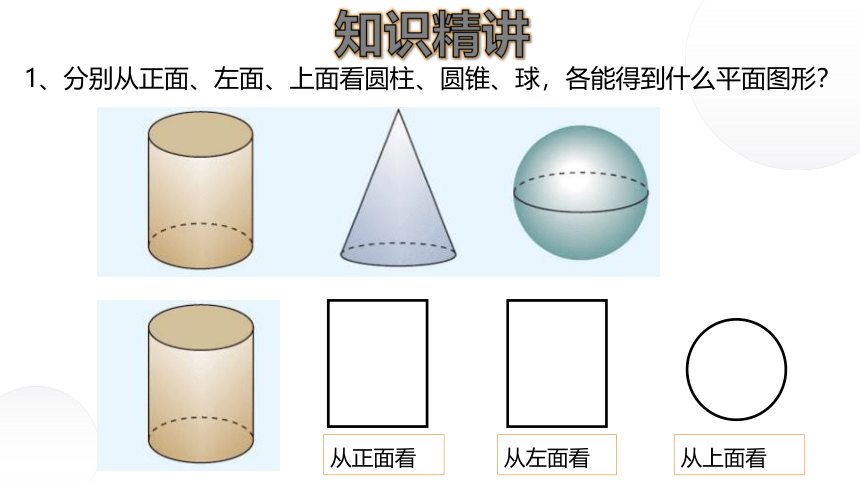
1、分别从正面、左面、上面看圆柱、圆锥、球,各能得到什么平面图形?
从上面看
从正面看
从左面看
知识精讲
从上面看
从正面看
从左面看
从上面看
从正面看
从左面看
练一练
1、分别从正面、左面、上面看下面几何体,各能得到什么平面图形?
从上面看
从正面看
从左面看
从上面看
从正面看
从左面看
从正面看
从左面看
从上面看
知识点二 立体图形的展开图
知识精讲
男孩子有没有折过飞机、纸船?
女孩子有没有折过千纸鹤、星星吗?
你还有折过什么吗?
思考:你能想象包装纸盒的展开图是什么样吗?
知识精讲
将一个长方体的表面沿某些棱剪开,能展成一个平面图形吗?你能得到哪些平面图形?与同伴进行交流.
案例 1:
案例 2:
案例 3:
知识精讲
将一个正方体的表面沿某些棱剪开,能展成一个平面图形吗?你能得到哪些平面图形?与同伴进行交流.
1
2
3
4
5
6
7
8
9
10
11
正方体的11种展开图
知识精讲
1.观察上面的11种正方体的展开图有没有什么规律?
2.小组讨论这些正方体展开图可以分为几类?哪几号展开图可以分为一类,为什么
问题
知识精讲
知识精讲
知识精讲
蓝
黄
红
正方体盒巧展开,
六个面儿七刀裁,
十一类图记分明;
中间四个成一行,
两边各一无规律;
二三紧连错一个,
三一相连一随意;
两两相连各错一,
三个两排一对齐;
对面相隔不相连,
识图巧排“凹”和“田”.
总结口诀
练一练
A B C D
C
1. 下列图形中,不是正方体表面展开图的是 ( )
2. “坚”在下,“就”在后,“胜”和“利”在哪里?
【点睛】一个多面体的展开图中,在同一直线上的相邻的三个线框中,首尾两个线框是立体图形中相对的两个面.
“胜”在上,“利”在前.
知识点三 根据从不同方向看到的图形还原几何体
知识精讲
1
1
2
2
不用摆出这个几何体,你能画出这个几何体的从正面看与从左面看的图吗?你能研究出上面看中的列与从正面看中的列有什么关系吗?每列的方块数又如何确定?
知识精讲
主视图:
左视图:
思考方法:
先根据上面看确定从正面看有几列,
3
再根据数字确定每列的方块有几个,
从正面看有 列,
第一列的方块有 个,
1
第二列的方块有 个,
2
第三列的方块有 个,
1
从左面看有 列,
2
第一列的方块有 个,
2
第二列的方块有 个,
2
1
1
2
2
典型例题
典例精析
【例1】从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
从左面看
从上面看
从正面看
解:
分析
从正面看有3列,从左往右,看到小方块的数量分别是1,2,1;
从左面看有1列,看到小方块的数量是2;
从上面看有3列,从左往右,看到小方块的数量都是1.
练一练
1、一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面、左面看到的这个几何体的形状图.
解:如图:
从正面看
从左面看
方法一:先摆出几何体,然后再画从正面看和从左面看到的形状图;
方法二:根据从上面看到的形状图及其各位置上小方块的个数,确定从正面看有2列,从左面看有2列,再根据数字确定每列方块的个数,进而画出从正面看和从左面看到的形状图.
分析
课堂练习
1.下面左图是两个长方体堆成的物体,则从正面看到的平面图形是( )
A
A.
C.
B.
D.
正面
2. 下图是由一些相同的小正方体构成的几何体的从正面、左面、上面看得到的三个平面图形,这些相同的小正方体的个数是 ( )
A.4个 B.5个 C.6个 D.7个
B
3.几个相同的正方体叠合在一起,该组合体的主视图和俯视图如图所示,那么组合体中正方体的个数至少有几个?至多有几个?( )
A.5,6 B.6,7 C.7,8 D.8,10
【详解】
解:第一层有1+2+3=6个正方体,第二层最少有2个正方体,
所以这个几何体最少有8个正方体组成;
第一层有1+2+3=6个正方体,第二层最多有4个正方体,
所以这个几何体最多有10个正方体组成.故答案为8,10.
4.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最多有
A.4 B.5 C.6 D.7
【解析】
由主视知这个几何体共有2层,由俯视图易得最底层有4个小正方体,由主视图可得二层最多有2个小正方体,第那么搭成这个几何体的小正方体最多为4+2=6个。故选C。
5.如图,是由一些棱长为1cm的小正方体构成的立体图形的三种视图,那么这个立体图形的表面积是( )
A.12 B.14 C.16 D.18
【详解】
由视图可得第一层有2个小正方体,第二层有1个小正方体,一共有3个,
表面积为:2×(2+2+3)=14cm2,
故选B.
6.将下图中平面展开图折叠成正方体后,相对面上的两个数之和都为6,则x=____,y=____.
1 2 3
x y
5
3
7、如图是一个几何体的三视图,若这个几何体的体积是30,则它的表面积是________.
【详解】∵由主视图得出长方体的长是5,宽是3,这个几何体的体积是30,
∴设高为h,则5×3×h=30,解得:h=2,
∴它的表面积是:5×3×2+5×2×2+3×2×2=30+20+12=62.
8、如图是一个几何体从三个方向看所得到的形状图.
(1)写出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)若从正面看的高为4cm,从上面看三角形的边长都为3 cm,求这个几何体的侧面积.
三棱柱
(3)3×4×3=36cm2,
∴这个几何体的侧面积为36 cm2
课堂总结
名称 立体图形 表面展开图 底面形状 侧面形状 侧面展开
图的形状
正方体 正方形 正方形 正方形
长方体 长方形 长方形 长方形
五棱柱 五边形 长方形 长方形
圆柱 圆 曲面 长方形
圆锥 圆 曲面 扇形
各类图形的表面展开图
课堂总结
正方体的展开图
正方体的11种展开图
展开图中对面、邻面的位置规律
第一类:141
第二类:132
第三类:222或33
一线不过四
田凹应弃之
间二、拐角邻面知
相间、Z端是对面
第四章 几何图形初步
4.1 几何图形
4.1.2 从不同的方向看立体图形和立体图形的展开图
学习目标
1、了解立体图形与平面图形之间的联系;
2、能画出简单立体图形从不同方向看得到的平面图形;
3、了解研究立体图形的方法,体会一个立体图形按照不同方式展开可得到不同的平面展开图;
4、通过展开与折叠,了解棱柱、棱锥、圆柱、圆锥、长方体、正方体的表面展开图或根据展开图判断立体图形;
情景引入
想一想:这是为什么呢?
从不同方向看山可看到“峰”,看到“岭”,那么从不同方向看几何体又能看到什么呢?你想知道吗?
现在就让我们一起来学习今天的“从三个方向看物体的形状”.
漫画“6”与“9”
思考:为什么他们会对同一个物体产生不同的看法?
知识点一 从不同方向看几何体
知识精讲
A
B
D
C
每台摄像机拍到的分别是下面的哪张照片?
B
A
C
D
当我们从不同的方向观察同一物体时,通常可以看到不同的图形.
知识精讲
下图是由小立方块搭成的几何体,从正面、左面、上面看到的几何体的形状是什么样的?
从左面看
从正面看
从左面看
从上面看
从正面看
从上面看
知识精讲
视图来自于投影.投影现象广泛存在于我们日常生活中,根据光源发出的光线不同,有中心投影和平行投影,如:灯光的光线可以看作是从一点发出的,我们称这种投影为中心投影;太阳的光线可以看是平行的,我们称这种投影为平行投影;视图是一种特殊的平行投影.
中心投影
平行投影
知识精讲
正面
侧面
水平面
主视图
俯视图
左视图
如图,从正面、上面和侧面(左面或右面)三个不同方向进行平行投影,可以的到三个投影,这样就可以用平面图形去刻画一个立体图形了.
从上面得到的投影,称为俯视图;
从侧面得到的投影,称为侧视图.
在正面得到的投影,称为主视图;
常把主视图、俯视图、左(或右)视图称做一个物体的三视图.
知识精讲
三视图的对应规律:
俯视图和左视图
主视图和俯视图
主视图和左视图
——长对正
——高平齐
——宽相等
主视图
俯视图
左视图
高
长
宽
宽
高平齐
长对正
宽相等
知识精讲
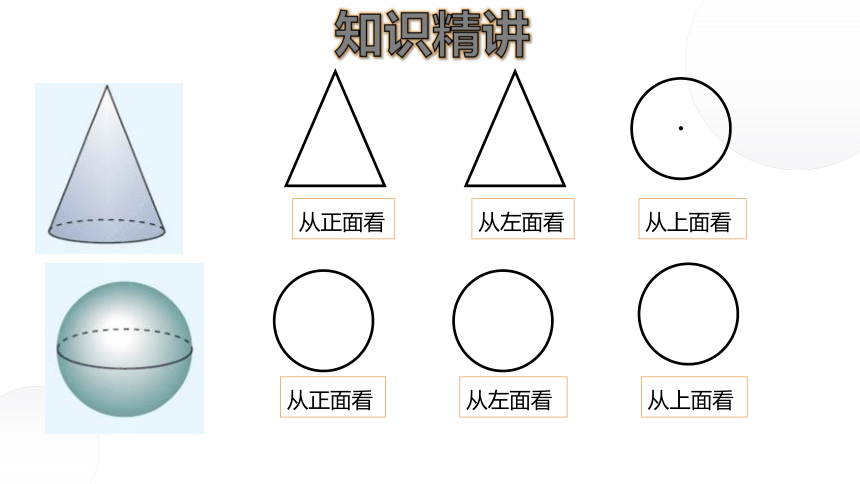
1、分别从正面、左面、上面看圆柱、圆锥、球,各能得到什么平面图形?
从上面看
从正面看
从左面看
知识精讲
从上面看
从正面看
从左面看
从上面看
从正面看
从左面看
练一练
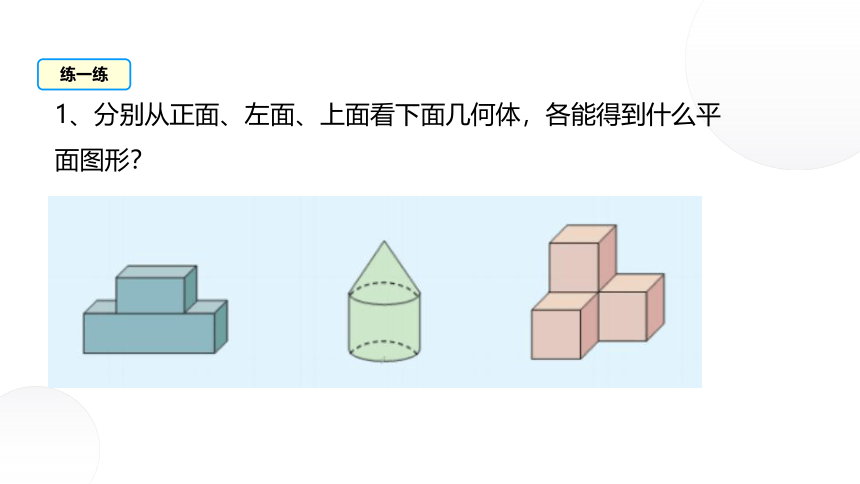
1、分别从正面、左面、上面看下面几何体,各能得到什么平面图形?
从上面看
从正面看
从左面看
从上面看
从正面看
从左面看
从正面看
从左面看
从上面看
知识点二 立体图形的展开图
知识精讲
男孩子有没有折过飞机、纸船?
女孩子有没有折过千纸鹤、星星吗?
你还有折过什么吗?
思考:你能想象包装纸盒的展开图是什么样吗?
知识精讲
将一个长方体的表面沿某些棱剪开,能展成一个平面图形吗?你能得到哪些平面图形?与同伴进行交流.
案例 1:
案例 2:
案例 3:
知识精讲
将一个正方体的表面沿某些棱剪开,能展成一个平面图形吗?你能得到哪些平面图形?与同伴进行交流.
1
2
3
4
5
6
7
8
9
10
11
正方体的11种展开图
知识精讲
1.观察上面的11种正方体的展开图有没有什么规律?
2.小组讨论这些正方体展开图可以分为几类?哪几号展开图可以分为一类,为什么
问题
知识精讲
知识精讲
知识精讲
蓝
黄
红
正方体盒巧展开,
六个面儿七刀裁,
十一类图记分明;
中间四个成一行,
两边各一无规律;
二三紧连错一个,
三一相连一随意;
两两相连各错一,
三个两排一对齐;
对面相隔不相连,
识图巧排“凹”和“田”.
总结口诀
练一练
A B C D
C
1. 下列图形中,不是正方体表面展开图的是 ( )
2. “坚”在下,“就”在后,“胜”和“利”在哪里?
【点睛】一个多面体的展开图中,在同一直线上的相邻的三个线框中,首尾两个线框是立体图形中相对的两个面.
“胜”在上,“利”在前.
知识点三 根据从不同方向看到的图形还原几何体
知识精讲
1
1
2
2
不用摆出这个几何体,你能画出这个几何体的从正面看与从左面看的图吗?你能研究出上面看中的列与从正面看中的列有什么关系吗?每列的方块数又如何确定?
知识精讲
主视图:
左视图:
思考方法:
先根据上面看确定从正面看有几列,
3
再根据数字确定每列的方块有几个,
从正面看有 列,
第一列的方块有 个,
1
第二列的方块有 个,
2
第三列的方块有 个,
1
从左面看有 列,
2
第一列的方块有 个,
2
第二列的方块有 个,
2
1
1
2
2
典型例题
典例精析
【例1】从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
从左面看
从上面看
从正面看
解:
分析
从正面看有3列,从左往右,看到小方块的数量分别是1,2,1;
从左面看有1列,看到小方块的数量是2;
从上面看有3列,从左往右,看到小方块的数量都是1.
练一练
1、一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面、左面看到的这个几何体的形状图.
解:如图:
从正面看
从左面看
方法一:先摆出几何体,然后再画从正面看和从左面看到的形状图;
方法二:根据从上面看到的形状图及其各位置上小方块的个数,确定从正面看有2列,从左面看有2列,再根据数字确定每列方块的个数,进而画出从正面看和从左面看到的形状图.
分析
课堂练习
1.下面左图是两个长方体堆成的物体,则从正面看到的平面图形是( )
A
A.
C.
B.
D.
正面
2. 下图是由一些相同的小正方体构成的几何体的从正面、左面、上面看得到的三个平面图形,这些相同的小正方体的个数是 ( )
A.4个 B.5个 C.6个 D.7个
B
3.几个相同的正方体叠合在一起,该组合体的主视图和俯视图如图所示,那么组合体中正方体的个数至少有几个?至多有几个?( )
A.5,6 B.6,7 C.7,8 D.8,10
【详解】
解:第一层有1+2+3=6个正方体,第二层最少有2个正方体,
所以这个几何体最少有8个正方体组成;
第一层有1+2+3=6个正方体,第二层最多有4个正方体,
所以这个几何体最多有10个正方体组成.故答案为8,10.
4.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最多有
A.4 B.5 C.6 D.7
【解析】
由主视知这个几何体共有2层,由俯视图易得最底层有4个小正方体,由主视图可得二层最多有2个小正方体,第那么搭成这个几何体的小正方体最多为4+2=6个。故选C。
5.如图,是由一些棱长为1cm的小正方体构成的立体图形的三种视图,那么这个立体图形的表面积是( )
A.12 B.14 C.16 D.18
【详解】
由视图可得第一层有2个小正方体,第二层有1个小正方体,一共有3个,
表面积为:2×(2+2+3)=14cm2,
故选B.
6.将下图中平面展开图折叠成正方体后,相对面上的两个数之和都为6,则x=____,y=____.
1 2 3
x y
5
3
7、如图是一个几何体的三视图,若这个几何体的体积是30,则它的表面积是________.
【详解】∵由主视图得出长方体的长是5,宽是3,这个几何体的体积是30,
∴设高为h,则5×3×h=30,解得:h=2,
∴它的表面积是:5×3×2+5×2×2+3×2×2=30+20+12=62.
8、如图是一个几何体从三个方向看所得到的形状图.
(1)写出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)若从正面看的高为4cm,从上面看三角形的边长都为3 cm,求这个几何体的侧面积.
三棱柱
(3)3×4×3=36cm2,
∴这个几何体的侧面积为36 cm2
课堂总结
名称 立体图形 表面展开图 底面形状 侧面形状 侧面展开
图的形状
正方体 正方形 正方形 正方形
长方体 长方形 长方形 长方形
五棱柱 五边形 长方形 长方形
圆柱 圆 曲面 长方形
圆锥 圆 曲面 扇形
各类图形的表面展开图
课堂总结
正方体的展开图
正方体的11种展开图
展开图中对面、邻面的位置规律
第一类:141
第二类:132
第三类:222或33
一线不过四
田凹应弃之
间二、拐角邻面知
相间、Z端是对面
