人教版8年级下册数学18.2.1 矩形 学案(含答案)
文档属性
| 名称 | 人教版8年级下册数学18.2.1 矩形 学案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 120.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 12:50:37 | ||
图片预览

文档简介
矩形
班级:_____________姓名:__________________组号:_________
矩形的性质
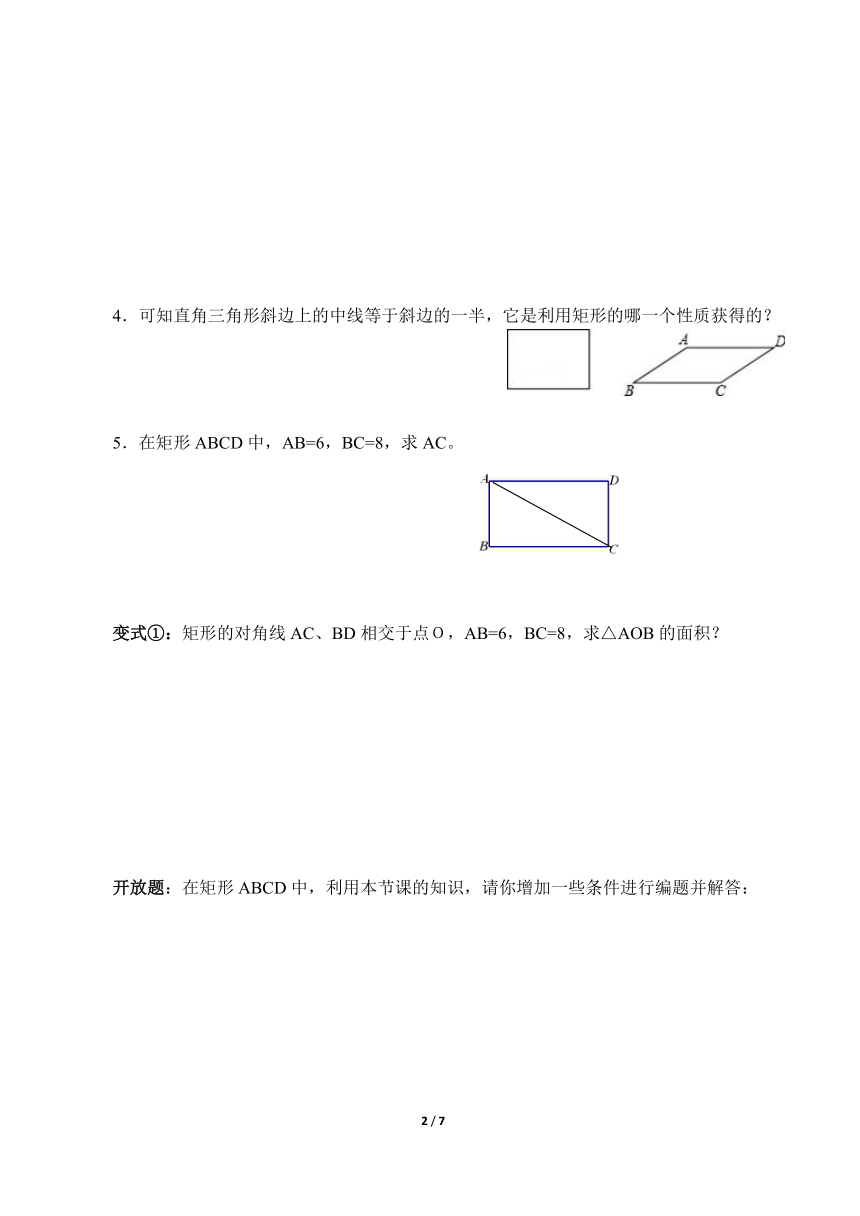
1.如图,ABCD中,写出平行四边形具有的性质?
2.什么叫矩形?用几何语言阐述你的理解:
3.矩形是特殊的平行四边形,它具备平行四边形的所有性质,下面再归纳出它的独特性质:
(1)矩形是轴对称图形吗?如果是,对称轴有几条?
(2)矩形的角、对角线有哪些特殊性质?
(3)对照旁边的图形,证明矩形的对角线相等这条性质。
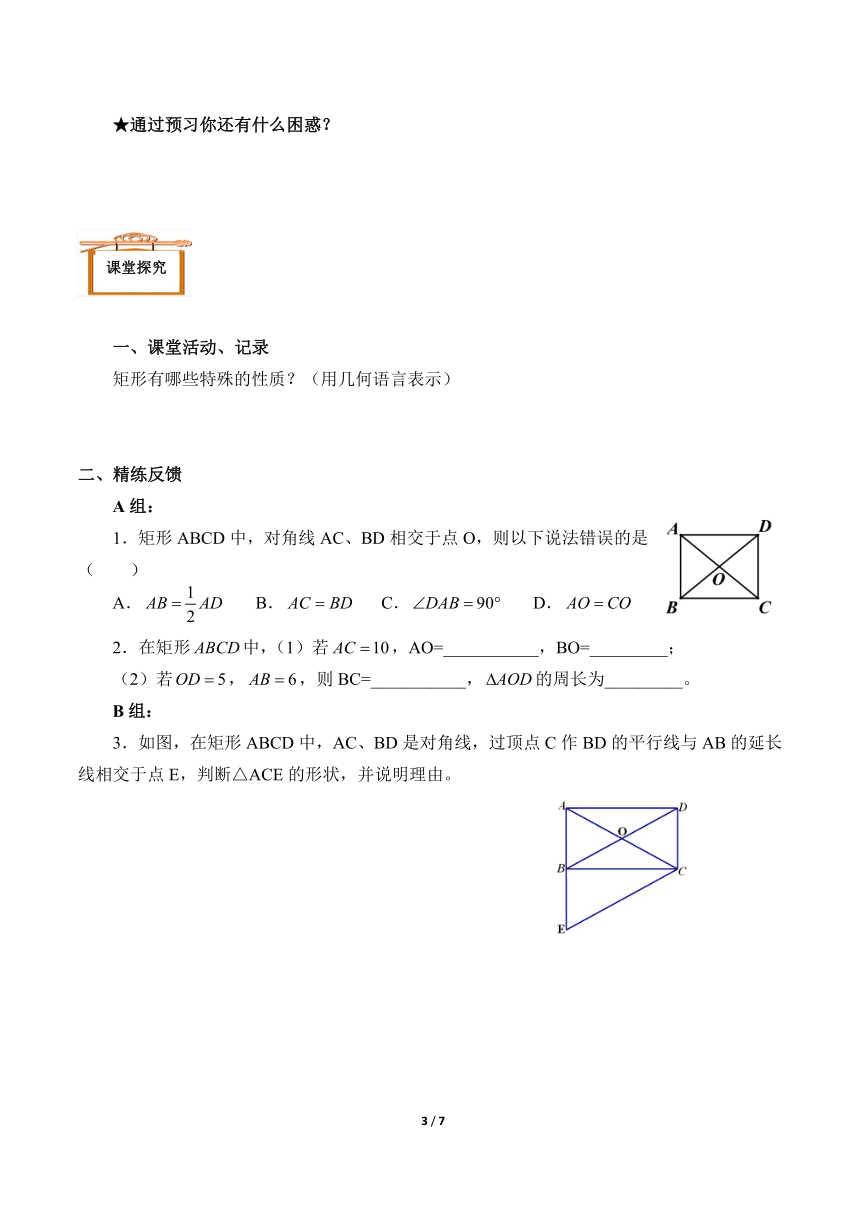
4.可知直角三角形斜边上的中线等于斜边的一半,它是利用矩形的哪一个性质获得的?
5.在矩形ABCD中,AB=6,BC=8,求AC。
变式①:矩形的对角线AC、BD相交于点O,AB=6,BC=8,求△AOB的面积?
开放题:在矩形ABCD中,利用本节课的知识,请你增加一些条件进行编题并解答:
★通过预习你还有什么困惑?
一、课堂活动、记录
矩形有哪些特殊的性质?(用几何语言表示)
二、精练反馈
A组:
1.矩形ABCD中,对角线AC、BD相交于点O,则以下说法错误的是( )
A. B. C. D.
2.在矩形中,(1)若,AO=___________,BO=_________;
(2)若,,则BC=___________,的周长为_________。
B组:
3.如图,在矩形ABCD中,AC、BD是对角线,过顶点C作BD的平行线与AB的延长线相交于点E,判断△ACE的形状,并说明理由。
三、课堂小结
1.矩形有哪些性质,直角三角形的性质。
2.你的其他收获。
四、拓展延伸(选做题)
1.将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的一半(木条宽度忽略不计),则这个平行四边形的最小内角为 度。
2.已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 ————————————————————。
3.如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,(1)求证:OE=OF;(2)若BC=2,求AB的长。
【答案】
【学前准备】
1.(1)平行四边形的两组对边分别平行且相等;
平行四边形两组对角分别相等;
平行四边形对角线互相平分
2.有一个角是直角的平行四边形是矩形,
∵四边形ABCD为平行四边形
又∠A=90°
∴平行四边形ABCD为矩形
3.(1)矩形是轴对称图形,对称轴有2条
(2)矩形4个角都是直角,矩形对角线相等且互相平分
(3)∵四边形ABCD为矩形
∴AB=CD,∠ABC=∠DCB
在△ABC和△DCB中
AB=CD,∠ABC=∠DCB,BC=CB
∴△ABC≌△DCB(S。A.S)
∴AC=BD
4.矩形的对角线相等且互相平分
5.连接AC
∵四边形ABCD为矩形∴∠ABC=90°
在Rt△ABC中
变式①:∵四边形ABCD为矩形∴∠ABC=90°
在Rt△ABC中
开放题:略
【课堂探究】
课堂活动、记录
略
精练反馈
1.A
2.(1)5;5(2)8;18
3.证明:∵四边形ABCD是矩形,
∴AC=BD,DC∥AE
∴DC∥BE
又BD∥EC
∴四边形BDCE是平行四边形
∴BD=EC.
∴AC=EC
∴△ACE是等腰三角形。
课堂小结
略
拓展延伸(选做题)
1.30
2.(3,4)、(2,4)
3.解:(1)证明:∵四边形ABCD是矩形,∴DC∥AB.
∴∠OAE=∠OCF,∠OEA=∠OFC
又∵AE=CF,∴△OEA≌△OFC(ASA)。
∴OE=OF。
如图,连接OB,
∵BE=BF,OE=OF,∴BO⊥EF,∠ABO=∠OBF。
∵△OEA≌△OFC ∴OA=OC
∵矩形ABCD中,∠ABC=90°,∴∠BOE=∠ABC=90°
在Rt△ABC中,
∵OA=OC=OB ∴∠OAB=∠OBA
∵∠BEF=2∠BAC,∴∠BEF=∠EBF
∴EF=BF ∴△BEF是等边三角形
作FG⊥AB,则FG=BC=OB=2
∴AC=2OB=4
在Rt△ABC中,
∴AB的长为6。
学前准备
课堂探究
7 / 7
班级:_____________姓名:__________________组号:_________
矩形的性质
1.如图,ABCD中,写出平行四边形具有的性质?
2.什么叫矩形?用几何语言阐述你的理解:
3.矩形是特殊的平行四边形,它具备平行四边形的所有性质,下面再归纳出它的独特性质:
(1)矩形是轴对称图形吗?如果是,对称轴有几条?
(2)矩形的角、对角线有哪些特殊性质?
(3)对照旁边的图形,证明矩形的对角线相等这条性质。
4.可知直角三角形斜边上的中线等于斜边的一半,它是利用矩形的哪一个性质获得的?
5.在矩形ABCD中,AB=6,BC=8,求AC。
变式①:矩形的对角线AC、BD相交于点O,AB=6,BC=8,求△AOB的面积?
开放题:在矩形ABCD中,利用本节课的知识,请你增加一些条件进行编题并解答:
★通过预习你还有什么困惑?
一、课堂活动、记录
矩形有哪些特殊的性质?(用几何语言表示)
二、精练反馈
A组:
1.矩形ABCD中,对角线AC、BD相交于点O,则以下说法错误的是( )
A. B. C. D.
2.在矩形中,(1)若,AO=___________,BO=_________;
(2)若,,则BC=___________,的周长为_________。
B组:
3.如图,在矩形ABCD中,AC、BD是对角线,过顶点C作BD的平行线与AB的延长线相交于点E,判断△ACE的形状,并说明理由。
三、课堂小结
1.矩形有哪些性质,直角三角形的性质。
2.你的其他收获。
四、拓展延伸(选做题)
1.将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的一半(木条宽度忽略不计),则这个平行四边形的最小内角为 度。
2.已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 ————————————————————。
3.如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,(1)求证:OE=OF;(2)若BC=2,求AB的长。
【答案】
【学前准备】
1.(1)平行四边形的两组对边分别平行且相等;
平行四边形两组对角分别相等;
平行四边形对角线互相平分
2.有一个角是直角的平行四边形是矩形,
∵四边形ABCD为平行四边形
又∠A=90°
∴平行四边形ABCD为矩形
3.(1)矩形是轴对称图形,对称轴有2条
(2)矩形4个角都是直角,矩形对角线相等且互相平分
(3)∵四边形ABCD为矩形
∴AB=CD,∠ABC=∠DCB
在△ABC和△DCB中
AB=CD,∠ABC=∠DCB,BC=CB
∴△ABC≌△DCB(S。A.S)
∴AC=BD
4.矩形的对角线相等且互相平分
5.连接AC
∵四边形ABCD为矩形∴∠ABC=90°
在Rt△ABC中
变式①:∵四边形ABCD为矩形∴∠ABC=90°
在Rt△ABC中
开放题:略
【课堂探究】
课堂活动、记录
略
精练反馈
1.A
2.(1)5;5(2)8;18
3.证明:∵四边形ABCD是矩形,
∴AC=BD,DC∥AE
∴DC∥BE
又BD∥EC
∴四边形BDCE是平行四边形
∴BD=EC.
∴AC=EC
∴△ACE是等腰三角形。
课堂小结
略
拓展延伸(选做题)
1.30
2.(3,4)、(2,4)
3.解:(1)证明:∵四边形ABCD是矩形,∴DC∥AB.
∴∠OAE=∠OCF,∠OEA=∠OFC
又∵AE=CF,∴△OEA≌△OFC(ASA)。
∴OE=OF。
如图,连接OB,
∵BE=BF,OE=OF,∴BO⊥EF,∠ABO=∠OBF。
∵△OEA≌△OFC ∴OA=OC
∵矩形ABCD中,∠ABC=90°,∴∠BOE=∠ABC=90°
在Rt△ABC中,
∵OA=OC=OB ∴∠OAB=∠OBA
∵∠BEF=2∠BAC,∴∠BEF=∠EBF
∴EF=BF ∴△BEF是等边三角形
作FG⊥AB,则FG=BC=OB=2
∴AC=2OB=4
在Rt△ABC中,
∴AB的长为6。
学前准备
课堂探究
7 / 7
