人教版8年级下册数学18.2.1 矩形 学案(无答案)
文档属性
| 名称 | 人教版8年级下册数学18.2.1 矩形 学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 129.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览

文档简介
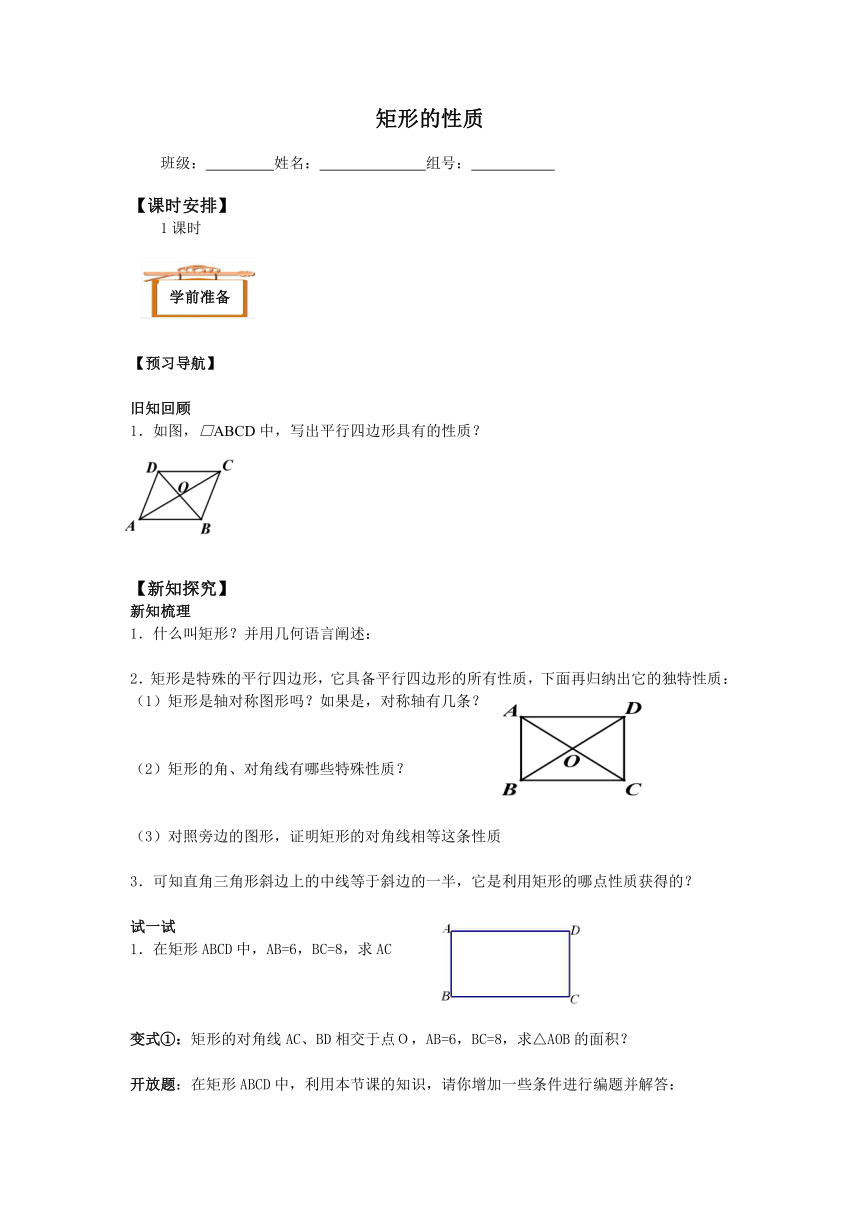
矩形的性质
班级: 姓名: 组号:
【课时安排】
1课时
【预习导航】
旧知回顾
1.如图,□ABCD中,写出平行四边形具有的性质?
【新知探究】
新知梳理
1.什么叫矩形?并用几何语言阐述:
2.矩形是特殊的平行四边形,它具备平行四边形的所有性质,下面再归纳出它的独特性质:
(1)矩形是轴对称图形吗?如果是,对称轴有几条?
(2)矩形的角、对角线有哪些特殊性质?
(3)对照旁边的图形,证明矩形的对角线相等这条性质
3.可知直角三角形斜边上的中线等于斜边的一半,它是利用矩形的哪点性质获得的?
试一试
1.在矩形ABCD中,AB=6,BC=8,求AC
变式①:矩形的对角线AC、BD相交于点O,AB=6,BC=8,求△AOB的面积?
开放题:在矩形ABCD中,利用本节课的知识,请你增加一些条件进行编题并解答:
★通过预习你还有什么困惑
课堂活动、记录
矩形有哪些特殊的性质?(用几何语言表示)
【精练反馈】
A组:
1.矩形ABCD中,对角线AC、BD相交于点O,则以下说法错误的是( )
A. B. C. D.
2.在矩形中,(1)若,,,
(2)若,,则,的周长为__________,
B组:
1.如图,在矩形ABCD中,AC、BD是对角线,过顶点C作BD的平行线与AB的延长线相交于点E,判断△ACE的形状,并说明理由。
【学习小结】
课堂小结
矩形有哪些性质,直角三角形的性质
【拓展延伸】
(选做题)
1. 将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的一半(木条宽度忽略不计),则这个平行四边形的最小内角为 度.
2.已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),
C(0,4),点D是OA的中点,点P在BC上运动,
当△ODP是腰长为5的等腰三角形时,
则P点的坐标为
3.如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC , (1)求证:OE=OF (2)若BC=2,求AB的长
班级: 姓名: 组号:
【课时安排】
1课时
【预习导航】
旧知回顾
1.如图,□ABCD中,写出平行四边形具有的性质?
【新知探究】
新知梳理
1.什么叫矩形?并用几何语言阐述:
2.矩形是特殊的平行四边形,它具备平行四边形的所有性质,下面再归纳出它的独特性质:
(1)矩形是轴对称图形吗?如果是,对称轴有几条?
(2)矩形的角、对角线有哪些特殊性质?
(3)对照旁边的图形,证明矩形的对角线相等这条性质
3.可知直角三角形斜边上的中线等于斜边的一半,它是利用矩形的哪点性质获得的?
试一试
1.在矩形ABCD中,AB=6,BC=8,求AC
变式①:矩形的对角线AC、BD相交于点O,AB=6,BC=8,求△AOB的面积?
开放题:在矩形ABCD中,利用本节课的知识,请你增加一些条件进行编题并解答:
★通过预习你还有什么困惑
课堂活动、记录
矩形有哪些特殊的性质?(用几何语言表示)
【精练反馈】
A组:
1.矩形ABCD中,对角线AC、BD相交于点O,则以下说法错误的是( )
A. B. C. D.
2.在矩形中,(1)若,,,
(2)若,,则,的周长为__________,
B组:
1.如图,在矩形ABCD中,AC、BD是对角线,过顶点C作BD的平行线与AB的延长线相交于点E,判断△ACE的形状,并说明理由。
【学习小结】
课堂小结
矩形有哪些性质,直角三角形的性质
【拓展延伸】
(选做题)
1. 将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的一半(木条宽度忽略不计),则这个平行四边形的最小内角为 度.
2.已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),
C(0,4),点D是OA的中点,点P在BC上运动,
当△ODP是腰长为5的等腰三角形时,
则P点的坐标为
3.如图,在矩形ABCD中,E、F分别是AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC , (1)求证:OE=OF (2)若BC=2,求AB的长
