4.1.1 第2课时从不同方向看立体图形及立体图形的展开图 课件(共34张PPT)
文档属性
| 名称 | 4.1.1 第2课时从不同方向看立体图形及立体图形的展开图 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 20:58:15 | ||
图片预览









文档简介
(共34张PPT)
人教七上数学同步精品课件
人教版七年级上册
第四章 几何图形初步
4.1.1第2课时 从不同方向看立体图形及立体图形的展开图
第1节 几何图形
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 能画出从不同方向看一些简单几何体以及由它们组成的简单组合体得到的平面图形.
2. 通过“展开”和“围成”两种途径认识常见几何图形.
3. 通过直观感知、操作等实践活动,丰富立体图形的认知和感受,进一步体会立体图形与平面图形之间的关系.
学习目标
重点
难点
新课引入
“横看成岭侧成峰”一句中,蕴含了怎样的数学道理
如图,把茶壶放在桌面上,那么下面五幅图片分别是从哪个方向看得到的?
从右面看
从左面看
从后面看
从上面看
从正面看
新知学习
从不同方向看立体图形,往往会得到不同形状的平面图形.
一般从三个方向看:
从正面看、
从左面看、
从上面看.
注意:
(1) 物体摆放方式不同,从同一方向看,得到的平面图形也会有所不同.
(2) 画从正面、左面、上面看一个几何体得到的平面图形时,画出的是示意图,只要形状相同,大小大致相当即可.
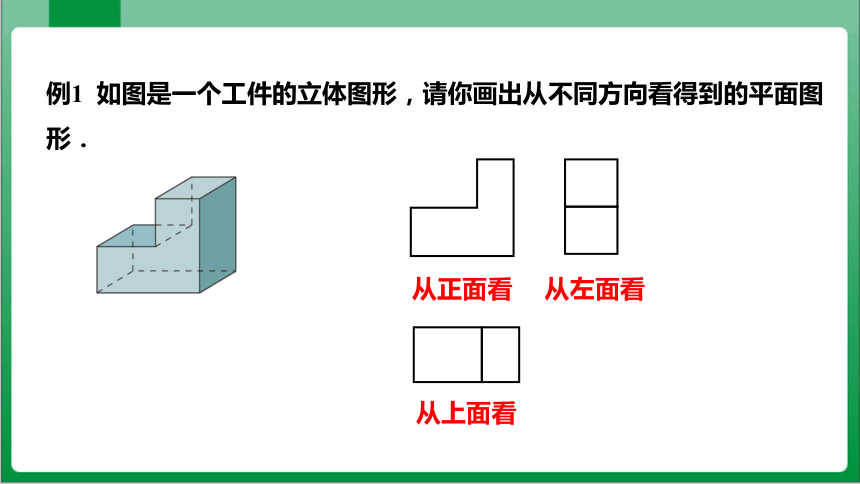
例1 如图是一个工件的立体图形,请你画出从不同方向看得到的平面图形.
从左面看
从上面看
从正面看
探究
如图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形各能得到什么平面图形?
从上面看
从左面看
从正面看
从正面看
从左面看
从上面看
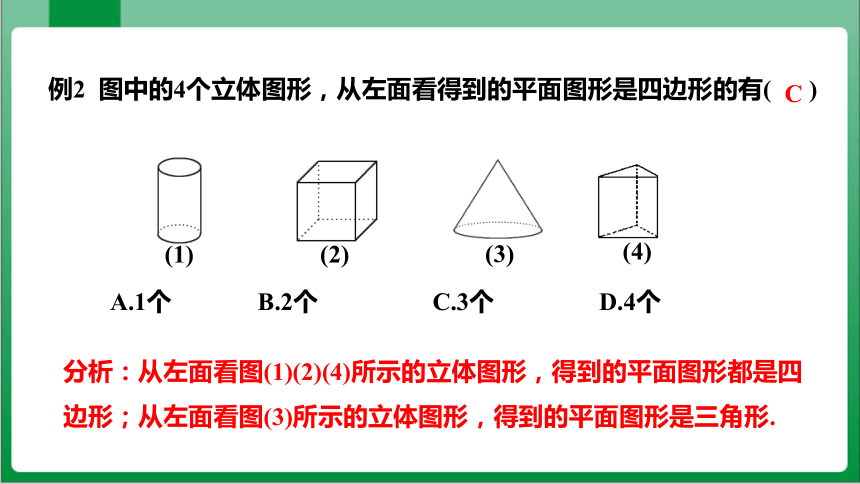
例2 图中的4个立体图形,从左面看得到的平面图形是四边形的有( )
分析:从左面看图(1)(2)(4)所示的立体图形,得到的平面图形都是四边形;从左面看图(3)所示的立体图形,得到的平面图形是三角形.
A.1个 B.2个 C.3个 D.4个
(3)
(1)
(2)
(4)
C
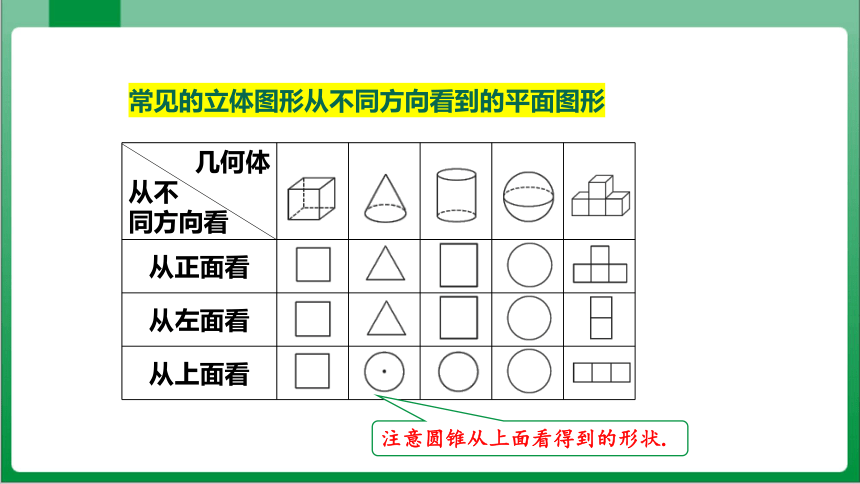
常见的立体图形从不同方向看到的平面图形
几何体 从不 同方向看
从正面看
从左面看
从上面看
注意圆锥从上面看得到的形状.
将一个正方体的表面适当剪开,能展开成哪些平面图形?
提示:沿着棱剪,展开后是一个平面图形.
观察与思考
立体图形的展开图:
有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形.这样的平面图形称为相应立体图形的展开图.
注意:(1) 同一个立体图形,按不同的方式展开,可能得到不同的平面图形,如正方体就有11种展开图.
(2) 不是所有的立体图形都有展开图,如球就没有展开图.
(3) 立体图形中相对的两个面在展开图中既没有公共边,也没有公共顶点.
常见立体图形的展开图
名称 正方体 长方体 五棱柱 圆柱 圆锥
立体图形
展开图(举例)
拓展
正方体的展开图
正方体的 11 种不同的展开图.
归纳
思考
能否将得到的平面图形分类?按什么规律来分类的?
第一类:1 — 4 — 1 型,共六种.
简记:中间 4 个连一串,两边各一随便放.
第二类:2 — 3 — 1 型,共三种.
简记:二三紧连错一个,三一相连一随便.
第三类: 2 — 2 — 2 型,只有一种.
第四类: 3 — 3 型,只有一种.
简记:两两相连各错一,三个两排一对齐.
例3 将一个无盖的正方体形状的盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )
C
分析:选项A,B,D中的平面图形都可以拼成无盖的正方体,但选项C中的平面图形拼成的是缺少两个面,且有一个面重合的“正方体”.
下面的平面图形是某些立体图形的展开图,请写出各平面图形所对应的立体图形的名称.
正方体
圆柱
三棱柱
圆锥
五棱柱
四棱锥
探究
(1) 展开图全是长方形或正方形时,要考虑长方体或正方体;
(2) 展开图中有三角形时,要考虑三棱柱或棱锥;
(3) 展开图中有长方形(或正方形)和圆时,要考虑圆柱;
(4) 展开图中有扇形时,要考虑圆锥.
根据展开图判断立体图形形状的方法:
随堂练习
1.正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是( )
A.厉 B.害 C.了 D.我
分析:由正方体的表面展开图的特征可得,“的”与“害”所在面是相对面,“了”与“厉”所在面是相对面,“我”与“国”所在面是相对面.
D
2.如图是一个几何体的表面展开图,则该几何体是( )
A.正方体 B.长方体
C.三棱柱 D.四棱锥
分析:由展开图知该几何体为棱柱,又底面为三角形,所以是三棱柱.
C
3.由若干个相同的小正方体搭成一个几何体,从不同方向观察该几何体所得到的平面图形如图所示,则搭成这个几何体所用小正方体的个数是( )
A.4 B.5 C.6 D.7
分析:由从上面看所得平面图形可以确定该几何体最底层有4个小正方体;由从正面看所得平面图形可以确定该几何体只有2层,且上面一层最多有2个小正方体;由从左面看所得平面图形可确定上面一层只有1个小正方体.所以搭成这个几何体所用小正方体的个数是4+1=5.
B
1.从不同方向看立体图形,往往会得到不同形状的平面图形.
一般从三个方向看:
从正面看、
从左面看、
从上面看.
课堂小结
2.有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展成平面图形. 这样的平面图形称为相应立体图形的展开图.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七上数学同步精品课件
人教版七年级上册
第四章 几何图形初步
4.1.1第2课时 从不同方向看立体图形及立体图形的展开图
第1节 几何图形
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 能画出从不同方向看一些简单几何体以及由它们组成的简单组合体得到的平面图形.
2. 通过“展开”和“围成”两种途径认识常见几何图形.
3. 通过直观感知、操作等实践活动,丰富立体图形的认知和感受,进一步体会立体图形与平面图形之间的关系.
学习目标
重点
难点
新课引入
“横看成岭侧成峰”一句中,蕴含了怎样的数学道理
如图,把茶壶放在桌面上,那么下面五幅图片分别是从哪个方向看得到的?
从右面看
从左面看
从后面看
从上面看
从正面看
新知学习
从不同方向看立体图形,往往会得到不同形状的平面图形.
一般从三个方向看:
从正面看、
从左面看、
从上面看.
注意:
(1) 物体摆放方式不同,从同一方向看,得到的平面图形也会有所不同.
(2) 画从正面、左面、上面看一个几何体得到的平面图形时,画出的是示意图,只要形状相同,大小大致相当即可.
例1 如图是一个工件的立体图形,请你画出从不同方向看得到的平面图形.
从左面看
从上面看
从正面看
探究
如图是一个由9个正方体组成的立体图形,分别从正面、左面、上面观察这个图形各能得到什么平面图形?
从上面看
从左面看
从正面看
从正面看
从左面看
从上面看
例2 图中的4个立体图形,从左面看得到的平面图形是四边形的有( )
分析:从左面看图(1)(2)(4)所示的立体图形,得到的平面图形都是四边形;从左面看图(3)所示的立体图形,得到的平面图形是三角形.
A.1个 B.2个 C.3个 D.4个
(3)
(1)
(2)
(4)
C
常见的立体图形从不同方向看到的平面图形
几何体 从不 同方向看
从正面看
从左面看
从上面看
注意圆锥从上面看得到的形状.
将一个正方体的表面适当剪开,能展开成哪些平面图形?
提示:沿着棱剪,展开后是一个平面图形.
观察与思考
立体图形的展开图:
有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形.这样的平面图形称为相应立体图形的展开图.
注意:(1) 同一个立体图形,按不同的方式展开,可能得到不同的平面图形,如正方体就有11种展开图.
(2) 不是所有的立体图形都有展开图,如球就没有展开图.
(3) 立体图形中相对的两个面在展开图中既没有公共边,也没有公共顶点.
常见立体图形的展开图
名称 正方体 长方体 五棱柱 圆柱 圆锥
立体图形
展开图(举例)
拓展
正方体的展开图
正方体的 11 种不同的展开图.
归纳
思考
能否将得到的平面图形分类?按什么规律来分类的?
第一类:1 — 4 — 1 型,共六种.
简记:中间 4 个连一串,两边各一随便放.
第二类:2 — 3 — 1 型,共三种.
简记:二三紧连错一个,三一相连一随便.
第三类: 2 — 2 — 2 型,只有一种.
第四类: 3 — 3 型,只有一种.
简记:两两相连各错一,三个两排一对齐.
例3 将一个无盖的正方体形状的盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )
C
分析:选项A,B,D中的平面图形都可以拼成无盖的正方体,但选项C中的平面图形拼成的是缺少两个面,且有一个面重合的“正方体”.
下面的平面图形是某些立体图形的展开图,请写出各平面图形所对应的立体图形的名称.
正方体
圆柱
三棱柱
圆锥
五棱柱
四棱锥
探究
(1) 展开图全是长方形或正方形时,要考虑长方体或正方体;
(2) 展开图中有三角形时,要考虑三棱柱或棱锥;
(3) 展开图中有长方形(或正方形)和圆时,要考虑圆柱;
(4) 展开图中有扇形时,要考虑圆锥.
根据展开图判断立体图形形状的方法:
随堂练习
1.正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是( )
A.厉 B.害 C.了 D.我
分析:由正方体的表面展开图的特征可得,“的”与“害”所在面是相对面,“了”与“厉”所在面是相对面,“我”与“国”所在面是相对面.
D
2.如图是一个几何体的表面展开图,则该几何体是( )
A.正方体 B.长方体
C.三棱柱 D.四棱锥
分析:由展开图知该几何体为棱柱,又底面为三角形,所以是三棱柱.
C
3.由若干个相同的小正方体搭成一个几何体,从不同方向观察该几何体所得到的平面图形如图所示,则搭成这个几何体所用小正方体的个数是( )
A.4 B.5 C.6 D.7
分析:由从上面看所得平面图形可以确定该几何体最底层有4个小正方体;由从正面看所得平面图形可以确定该几何体只有2层,且上面一层最多有2个小正方体;由从左面看所得平面图形可确定上面一层只有1个小正方体.所以搭成这个几何体所用小正方体的个数是4+1=5.
B
1.从不同方向看立体图形,往往会得到不同形状的平面图形.
一般从三个方向看:
从正面看、
从左面看、
从上面看.
课堂小结
2.有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展成平面图形. 这样的平面图形称为相应立体图形的展开图.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
