2023—2024学年北师大版数学七年级下册1.6完全平方公式(1)课件(共32张PPT)
文档属性
| 名称 | 2023—2024学年北师大版数学七年级下册1.6完全平方公式(1)课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 399.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
学习口号
一二三四五,学习不怕苦;
一二三四五,学习要专注;
一二三四五,坚持有进步;
一二三四五,进步不停步。
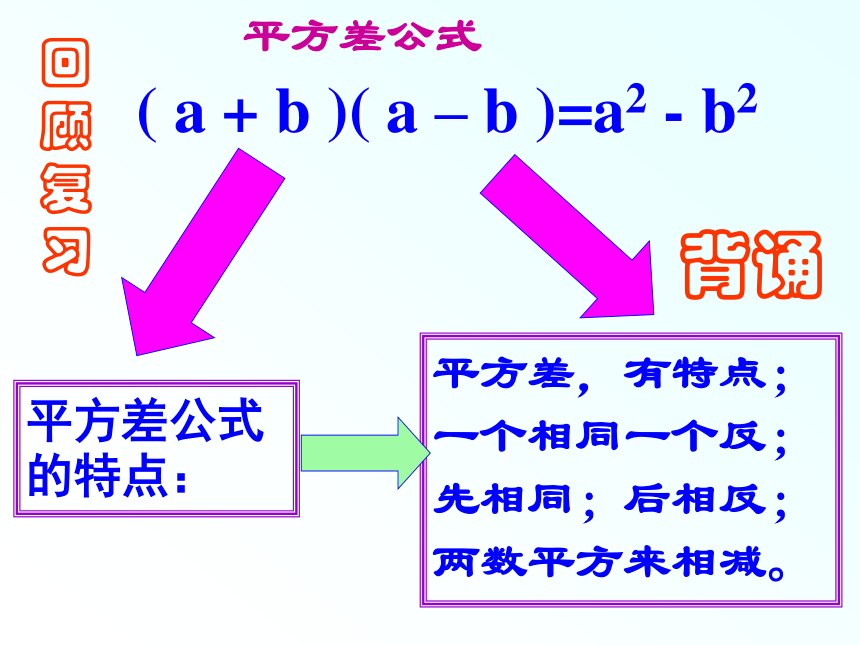
平方差公式
平方差公式的特点:
平方差,有特点;
一个相同一个反;
先相同;后相反;
两数平方来相减。
背诵
回顾复习
( a + b )( a – b )=a2 - b2
①(x + 10) ( x-10)
②(—7 + 2a) ( —7-2a)
③(2m+ 3n) ( 2m-3n)
④(—5y — 2x ) (5y —2x )
算一算,比一比,看谁算得又快又准
1.6 完全平方公式(1)
学习新课
计算下列各式,你能发现什么?
(p+1)2 =(p+1)(p+1)=
(m+2)2 =
(p-1)2 =(p-1)(p-1)=
(m-2)2 =
p2+2p+1
(m+2)(m+2)= m2+4m+4
p2-2p+1
(m-2)(m-2)= m2- 4m+4
计算下列各式,你能发现什么?
(p+1)2 =
(m+2)2=
(p-1)2 =
(m-2)2 =
p2+2p+1=p2+2×p×1+12
m2+4m+4=m2+2×m×2+22
p2-2p+1=p2-2×p×1+12
m2- 4m+4=m2-2×m×2+22
猜想 (a+b)2=
(a -b)2=
a2+2ab+b2
a2 - 2ab+b2
验证: (a+b)2, (a- b)2
解: (a+b)2= (a+b) (a+b)
=a2+ab+ab+b2
=a2+2ab+b2
(a-b)2= (a-b) (a-b)
=a2-ab-ab+b2
=a2-2ab+b2
b
b
a
a
(a+b)
a
b
ab
ab
+
+
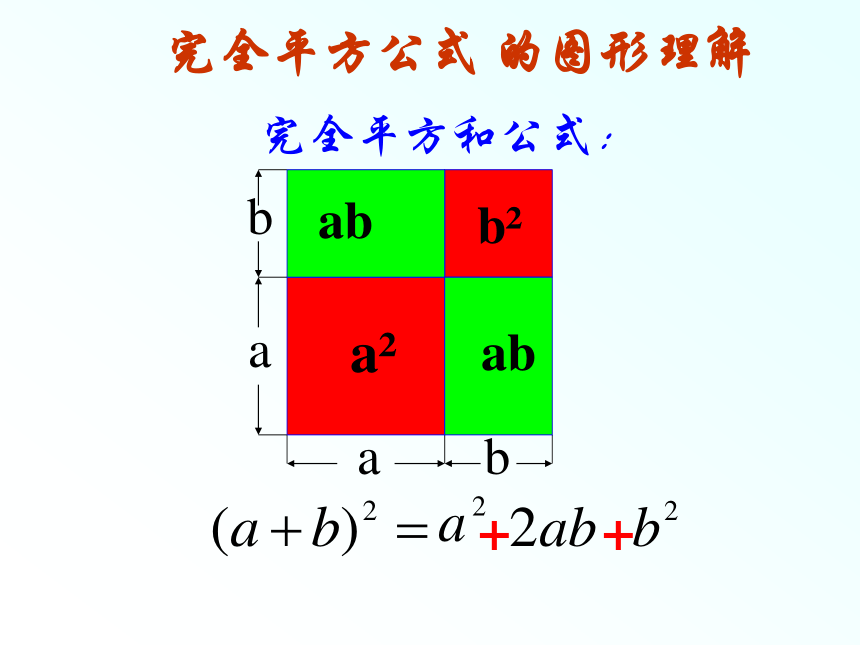
完全平方和公式:
完全平方公式 的图形理解
a
a
b
b
(a-b)
a
ab
ab
b
b
b
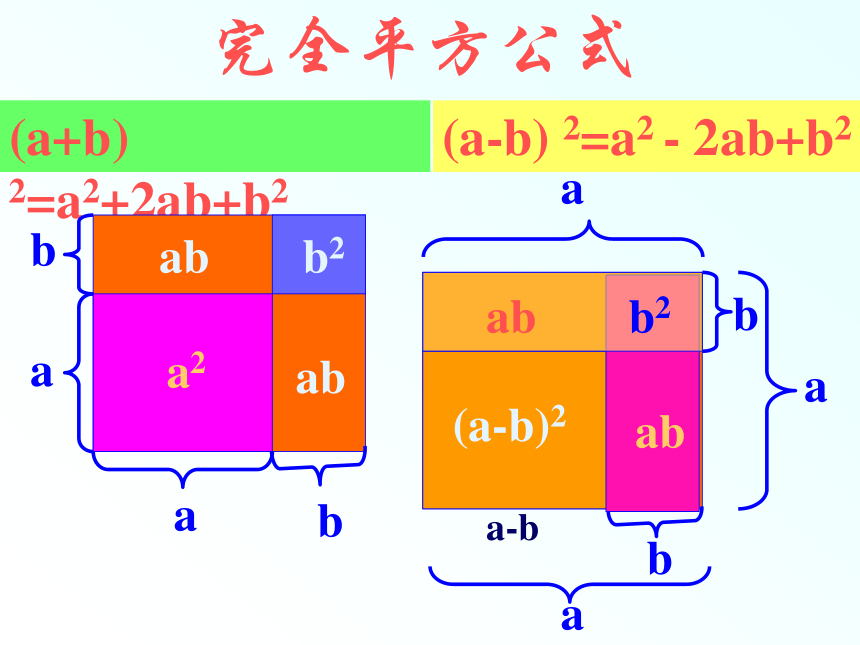
完全平方差公式:
完全平方公式 的图形理解
完全平方公式
(a+b) 2=a2+2ab+b2
(a-b) 2=a2 - 2ab+b2
b
b
a
a
ab
ab
a2
b2
b
a
b
a
(a-b)2
ab
ab
b2
a
a-b
公式特点:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
亲们,
背过啊。
背写3遍
完全平方有 3 项,
首平方,尾平方,
首尾2倍放中央。
中央符号看端详。
【例1】运用完全平方公式计算:
【解析】
=x2
(1)(x+2y)2
(a + b)2 = a2 + 2 a b + b2
x2
+2 x 2y
+ (2y)2
+4xy
+4y2
【例题】
(x + 2y)2 =
例1 运用完全平方公式计算:
解: (x-2y)2=
=x2
(2)(x-2y)2
(a - b)2= a2 - 2 ab + b2
x2
-2 x 2y
+(2y)2
-4xy
+4y2
(a+b)2=a2+2ab+b2, (a -b)2 =a2-2ab+b2
例1.计算: (x+2y)2, (x-2y)2
解: (x+2y)2=
( a+ b)2=a2+2 a b+ b2
=x2+4xy+4y2
(x - 2y )2=
(a - b )2 =a2 - 2 a b + b2
x2 - 2· x· 2y +( 2y )2
x2+2·x·2y+(2y)2
=x2 - 4xy+4y2
(1)(x+2y)2 =
(2)(4-y)2 =
(3)(2m-n)2=
算一算
解:1) (4a-b)2 = (4a)2-2·4a·b+b2
= 16a2-8ab+b2
例2.运用完全平方公式计算:
1) (4a-b)2 2) (y+ )2
2) (y+ )2
= y2+y+
=y2+2·y· +( )2
随堂练习
运用完全平方公式计算:
(-2x+5)2
(n +1)2 n2.
(1) ( x 2y)2 ;
(2) (2xy+ x )2 ;
亲,你会吗?
1.运用完全平方公式计算:
(1)(x+6)2; (2) (y-5)2;
(3) (-2x+5)2; (4) ( x - y)2.
基础练习:
思考
(3) (a+b)2与(-a-b)2相等吗
(1) (a-b)2与(b-a)2相等吗
(2) (-a+b)2与(b-a)2相等吗
下列等式是否成立?说明理由。
⑴
⑵
(-a-b)2
(a-b)2
诊断
√
√
=(a+b)2
=(b-a)2
(-a+b)2
=(b-a)2
(1) (6a+5b)2
=36a2+60ab+25b2
(2)(4x-3y)2
=16x2-24xy+9y2
(3) (2m-1)2
=4m2-4m+1
(4)(-2m-1)2
=4m2+4m+1
亲,你会吗?
【例3】运用完全平方公式计算:
(1) 1022; (2) 992.
(1) 1022 = (100 +2)2
= 1002 +2×100×2 + 22
= 10 000 +400 +4
= 10 404
(2) 992 = (100 -1)2
= 1002 -2×100×1+12
= 10 000 - 200 + 1
= 9 801
【例3】运用完全平方公式计算:
(1) 1022; (2) 992.
1992=
8.92=
利用完全平方公式计算:
1012=
(1)若x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
(2)将正方形的边长由a增加6,
则正方形的面积增加了( )
A.36 B.12a
C.36+12a D.以上都不对
c
c
亲,你会吗?
(3).若x2-6x+N是完全平方式,则N是( )
(A ) 11 (B) 9 (C) -11 (D) -9
B
(4)小贾计算二项整式的完全平方式时, 得到正确结果是4x2 + _____ + 25y2, 但中间一项不慎被污染了,这一项应是( )
A 10xy B 20xy C±10xy D±20xy
D
你不会?
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
(1)如果x2+kx+25是完全平方式,
则 k =_____.
±5
(2)如果9x2-mxy+16y 可化为一个
整式的平方,则 m =_____.
2
±24
你会吗?
1. =_______;
2.若 是一个完全平方公式, 则 _______;
3.若 是一个完全平方公式,则 _______;
1
亲,你会吗?
亲们
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
完全平方有 3 项,
首平方,尾平方,
首尾2倍放中央。
中央符号看端详。
亲们
再背2遍
最后 再写2遍
亲,会填空吗?
1) a2+ +b2=(a+b)2
2) a2+ +b2=(a - b)2
3) 4a2+ +b2=(2a+b)2
4) 4a2+ +b2=(2a - b)2
5) ( )2+4ab+b2=( +b)2
6) a2-8ab+ =( )2
2ab
(-2ab)
4ab
(-4ab)
2a
2a
16b2
a-4b
计算:(x+3)2-x2.
你有几种解法?
【解法1】
(x+3)2-x2.
=(x+3+x)(x+3-x)
=(2x+3)×3
=6x+9.
【解法2】
(x+3)2-x2.
=x2+6x+9-x2
=6x+9.
逆用平方差公式
用完全平方公式
学习口号
一二三四五,学习不怕苦;
一二三四五,学习要专注;
一二三四五,坚持有进步;
一二三四五,进步不停步。
平方差公式
平方差公式的特点:
平方差,有特点;
一个相同一个反;
先相同;后相反;
两数平方来相减。
背诵
回顾复习
( a + b )( a – b )=a2 - b2
①(x + 10) ( x-10)
②(—7 + 2a) ( —7-2a)
③(2m+ 3n) ( 2m-3n)
④(—5y — 2x ) (5y —2x )
算一算,比一比,看谁算得又快又准
1.6 完全平方公式(1)
学习新课
计算下列各式,你能发现什么?
(p+1)2 =(p+1)(p+1)=
(m+2)2 =
(p-1)2 =(p-1)(p-1)=
(m-2)2 =
p2+2p+1
(m+2)(m+2)= m2+4m+4
p2-2p+1
(m-2)(m-2)= m2- 4m+4
计算下列各式,你能发现什么?
(p+1)2 =
(m+2)2=
(p-1)2 =
(m-2)2 =
p2+2p+1=p2+2×p×1+12
m2+4m+4=m2+2×m×2+22
p2-2p+1=p2-2×p×1+12
m2- 4m+4=m2-2×m×2+22
猜想 (a+b)2=
(a -b)2=
a2+2ab+b2
a2 - 2ab+b2
验证: (a+b)2, (a- b)2
解: (a+b)2= (a+b) (a+b)
=a2+ab+ab+b2
=a2+2ab+b2
(a-b)2= (a-b) (a-b)
=a2-ab-ab+b2
=a2-2ab+b2
b
b
a
a
(a+b)
a
b
ab
ab
+
+
完全平方和公式:
完全平方公式 的图形理解
a
a
b
b
(a-b)
a
ab
ab
b
b
b
完全平方差公式:
完全平方公式 的图形理解
完全平方公式
(a+b) 2=a2+2ab+b2
(a-b) 2=a2 - 2ab+b2
b
b
a
a
ab
ab
a2
b2
b
a
b
a
(a-b)2
ab
ab
b2
a
a-b
公式特点:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
亲们,
背过啊。
背写3遍
完全平方有 3 项,
首平方,尾平方,
首尾2倍放中央。
中央符号看端详。
【例1】运用完全平方公式计算:
【解析】
=x2
(1)(x+2y)2
(a + b)2 = a2 + 2 a b + b2
x2
+2 x 2y
+ (2y)2
+4xy
+4y2
【例题】
(x + 2y)2 =
例1 运用完全平方公式计算:
解: (x-2y)2=
=x2
(2)(x-2y)2
(a - b)2= a2 - 2 ab + b2
x2
-2 x 2y
+(2y)2
-4xy
+4y2
(a+b)2=a2+2ab+b2, (a -b)2 =a2-2ab+b2
例1.计算: (x+2y)2, (x-2y)2
解: (x+2y)2=
( a+ b)2=a2+2 a b+ b2
=x2+4xy+4y2
(x - 2y )2=
(a - b )2 =a2 - 2 a b + b2
x2 - 2· x· 2y +( 2y )2
x2+2·x·2y+(2y)2
=x2 - 4xy+4y2
(1)(x+2y)2 =
(2)(4-y)2 =
(3)(2m-n)2=
算一算
解:1) (4a-b)2 = (4a)2-2·4a·b+b2
= 16a2-8ab+b2
例2.运用完全平方公式计算:
1) (4a-b)2 2) (y+ )2
2) (y+ )2
= y2+y+
=y2+2·y· +( )2
随堂练习
运用完全平方公式计算:
(-2x+5)2
(n +1)2 n2.
(1) ( x 2y)2 ;
(2) (2xy+ x )2 ;
亲,你会吗?
1.运用完全平方公式计算:
(1)(x+6)2; (2) (y-5)2;
(3) (-2x+5)2; (4) ( x - y)2.
基础练习:
思考
(3) (a+b)2与(-a-b)2相等吗
(1) (a-b)2与(b-a)2相等吗
(2) (-a+b)2与(b-a)2相等吗
下列等式是否成立?说明理由。
⑴
⑵
(-a-b)2
(a-b)2
诊断
√
√
=(a+b)2
=(b-a)2
(-a+b)2
=(b-a)2
(1) (6a+5b)2
=36a2+60ab+25b2
(2)(4x-3y)2
=16x2-24xy+9y2
(3) (2m-1)2
=4m2-4m+1
(4)(-2m-1)2
=4m2+4m+1
亲,你会吗?
【例3】运用完全平方公式计算:
(1) 1022; (2) 992.
(1) 1022 = (100 +2)2
= 1002 +2×100×2 + 22
= 10 000 +400 +4
= 10 404
(2) 992 = (100 -1)2
= 1002 -2×100×1+12
= 10 000 - 200 + 1
= 9 801
【例3】运用完全平方公式计算:
(1) 1022; (2) 992.
1992=
8.92=
利用完全平方公式计算:
1012=
(1)若x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
(2)将正方形的边长由a增加6,
则正方形的面积增加了( )
A.36 B.12a
C.36+12a D.以上都不对
c
c
亲,你会吗?
(3).若x2-6x+N是完全平方式,则N是( )
(A ) 11 (B) 9 (C) -11 (D) -9
B
(4)小贾计算二项整式的完全平方式时, 得到正确结果是4x2 + _____ + 25y2, 但中间一项不慎被污染了,这一项应是( )
A 10xy B 20xy C±10xy D±20xy
D
你不会?
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
(1)如果x2+kx+25是完全平方式,
则 k =_____.
±5
(2)如果9x2-mxy+16y 可化为一个
整式的平方,则 m =_____.
2
±24
你会吗?
1. =_______;
2.若 是一个完全平方公式, 则 _______;
3.若 是一个完全平方公式,则 _______;
1
亲,你会吗?
亲们
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
完全平方有 3 项,
首平方,尾平方,
首尾2倍放中央。
中央符号看端详。
亲们
再背2遍
最后 再写2遍
亲,会填空吗?
1) a2+ +b2=(a+b)2
2) a2+ +b2=(a - b)2
3) 4a2+ +b2=(2a+b)2
4) 4a2+ +b2=(2a - b)2
5) ( )2+4ab+b2=( +b)2
6) a2-8ab+ =( )2
2ab
(-2ab)
4ab
(-4ab)
2a
2a
16b2
a-4b
计算:(x+3)2-x2.
你有几种解法?
【解法1】
(x+3)2-x2.
=(x+3+x)(x+3-x)
=(2x+3)×3
=6x+9.
【解法2】
(x+3)2-x2.
=x2+6x+9-x2
=6x+9.
逆用平方差公式
用完全平方公式
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
