人教版数学8年级上册 12.2 三角形全等的判定 学案(无答案)
文档属性
| 名称 | 人教版数学8年级上册 12.2 三角形全等的判定 学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 177.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览



文档简介
三角形全等的判定
【课时安排】
4课时。
【第一课时】
【学习目标】
1.掌握“边边边”的条件内容。
2.能初步应用“SSS”条件判定两个三角形全等。
3.会作一个角等于已知角。
4.经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
【学习重难点】
1.“边边边”的条件。
2.探索三角形全等的条件。
【学习过程】
一、复习巩固。
已知△ABC≌△DEF,找出其中相等的边和角。
思考:
1.满足这六个条件,可以保证△ABC≌△DEF吗?
2.如果只满足这六个条件中的一部分,那么能保证△ABC≌△DEF吗?
二、探究新知。
分情况讨论:(要求学生画出符合要求的三角形,同桌相互比较)
1.只给一个条件。
①只给一条边②只给一个角。
2.满足两个条件。
①两边②一边一角③两角。
结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。
3.满足三个条件。
①三角②三边③两边一角④两角一边。
已知两个三角形的三个内角分别为30°,60°,90°,它们一定全等吗?
三、应用新知。
如图,三角形钢架中,AB=AC,AD是连接A与BC中点的支架,求证△ABD≌△ACD。
归纳:证明的书写步骤。
①准备条件:证全等时要用的条件要先证好。
②三角形全等书写三步骤:写出在哪两个三角形中;摆出三个条件用大括号括起来;写出全等结论。
四、变式练习。
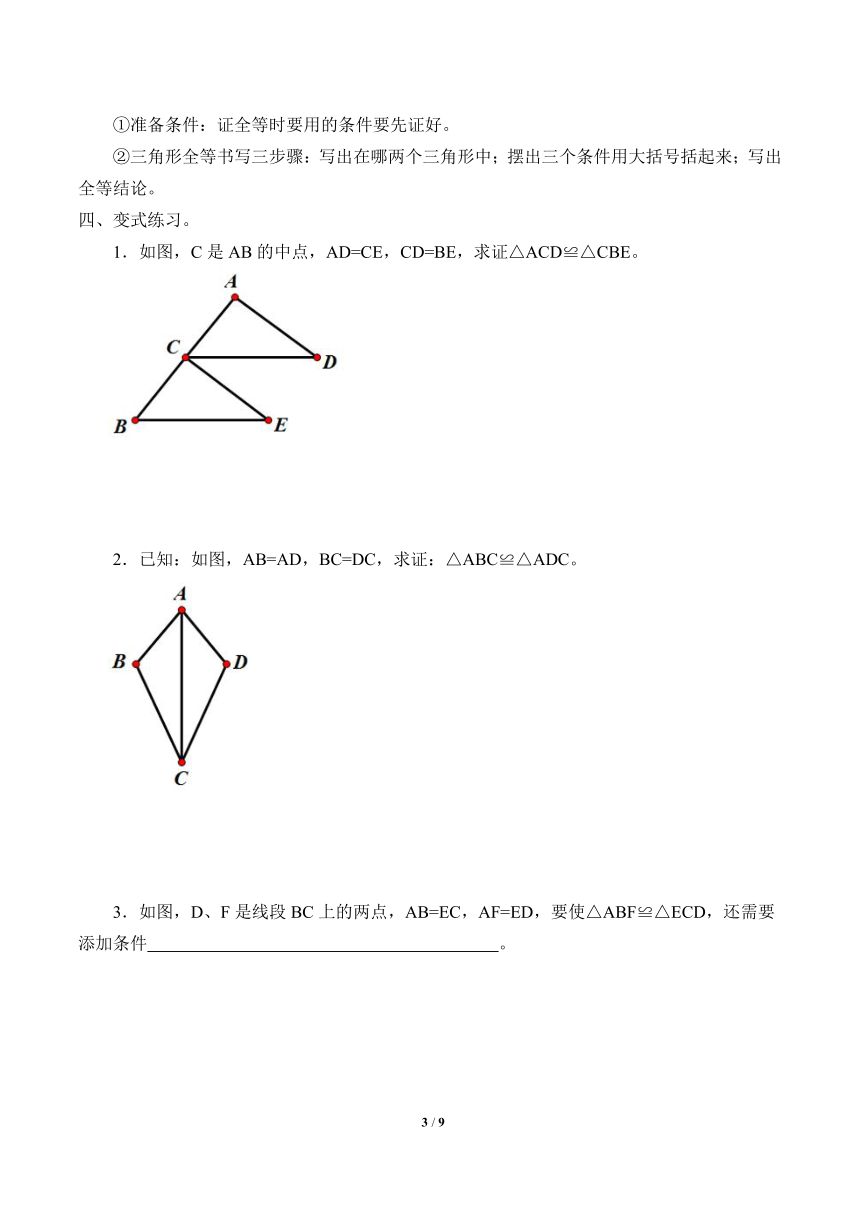
1.如图,C是AB的中点,AD=CE,CD=BE,求证△ACD≌△CBE。
2.已知:如图,AB=AD,BC=DC,求证:△ABC≌△ADC。
3.如图,D、F是线段BC上的两点,AB=EC,AF=ED,要使△ABF≌△ECD,还需要添加条件 。
【第二课时】
【学习目标】
1.掌握“SAS”的判定方法。
2.能初步应用“边角边”条件判定两个三角形全等。
3.经历探索三角形全等的过程,体验操作,归纳得出数学结论的过程。
【学习重难点】
1.“边角边”条件的理解和应用。
2.学会分析问题,寻找判定三角形全等的条件。
【学习过程】
一、创设情境。
上节课学习了三角形全等的判定定理边边边,除此之外,判定三角形全等还有没有其他方法?
二、探究指导。
思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能呢?
三、应用新知。
如图:有一池塘,要测池塘两端A,B的距离,可先在平底上取一点C,从点C不经过池塘可以直接到达点A和点B,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE,那么量出DE的长就是A,B的距离,为什么?
四、变式练习。
1.如图,两车从南北方向的路段AB的A端出发,分别向东,向西行进相同的距离,到达C、D两地,此时C、D到B的距离相等吗?为什么?
2.如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,求证∠A=∠D。
3.如图,已知AB=AC,点D、E分别是AB和AC上的点,且DB=EC,求证∠B=∠C。
【第三课时】
【学习目标】
1.掌握“角边角”及“角角边”条件内容。
2.能初步应用“角边角”及“角角边”条件判定两个三角形全等。
3.经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
【学习重难点】
1.“角边角”条件及“角角边”条件。
2.分析问题,寻找判定两个三角形全等的条件。
【学习过程】
一、复习导入。
思考我们已经会哪些条件判定两个三角形全等?
二、探究新知。
思考:师提问,两个角和其中一个角的对边对角相等的两个三角形全等吗?
师出示多媒体:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF(如下图),△ABC和△DEF全等吗?你能用角边角证明得到的结论吗?
生分小组讨论证明,师巡视指导,将一个学生的证明过程展台展示,师生共同纠正,后师生共同总结。
三、应用新知。
如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C。求证:AD=AE。
总结:两角和其中一个角的对边分别相等的两个三角形全等(AAS)。
四、变式练习。
1.要测量池塘两岸相对的两点A、B的距离,在池塘外取AB的垂线BF上的两点C,D,使BC=CD,在画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
2.如图,点D在AB上,点E在AC上,∠B=∠C,那么补充下列哪一个条件后,仍无法判定△ABE≌△ACD?( )
A.AD=AE B.∠AEB=∠ADC
C.BE=CD D.AB=AC
【第四课时】
【学习目标】
1.探索掌握直角三角形全等的条件:“斜边,直角边”。
2.经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
3.充分调动积极性,增强自信心。
【学习重难点】
1.探究直角三角形全等的条件。
2.灵活运用直角三角形全等的条件进行证明。
【学习过程】
一、复习巩固。
我们已经学过了哪些判定三角形全等的方法?
二、情境诱导。
对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?
三、探究新知。
师出示多媒体:任意画一个Rt△ABC,使∠C=90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,把画好的Rt△A′B′C′剪下,放到Rt△ABC上,它们全等吗?
四、应用新知。
如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD。求证:BC=AD。
五、变式练习。
1.如图,C是路段AB的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D、E两地,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?
2.如图,AB=AD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF,求证:AE=DF。
9 / 9
【课时安排】
4课时。
【第一课时】
【学习目标】
1.掌握“边边边”的条件内容。
2.能初步应用“SSS”条件判定两个三角形全等。
3.会作一个角等于已知角。
4.经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
【学习重难点】
1.“边边边”的条件。
2.探索三角形全等的条件。
【学习过程】
一、复习巩固。
已知△ABC≌△DEF,找出其中相等的边和角。
思考:
1.满足这六个条件,可以保证△ABC≌△DEF吗?
2.如果只满足这六个条件中的一部分,那么能保证△ABC≌△DEF吗?
二、探究新知。
分情况讨论:(要求学生画出符合要求的三角形,同桌相互比较)
1.只给一个条件。
①只给一条边②只给一个角。
2.满足两个条件。
①两边②一边一角③两角。
结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。
3.满足三个条件。
①三角②三边③两边一角④两角一边。
已知两个三角形的三个内角分别为30°,60°,90°,它们一定全等吗?
三、应用新知。
如图,三角形钢架中,AB=AC,AD是连接A与BC中点的支架,求证△ABD≌△ACD。
归纳:证明的书写步骤。
①准备条件:证全等时要用的条件要先证好。
②三角形全等书写三步骤:写出在哪两个三角形中;摆出三个条件用大括号括起来;写出全等结论。
四、变式练习。
1.如图,C是AB的中点,AD=CE,CD=BE,求证△ACD≌△CBE。
2.已知:如图,AB=AD,BC=DC,求证:△ABC≌△ADC。
3.如图,D、F是线段BC上的两点,AB=EC,AF=ED,要使△ABF≌△ECD,还需要添加条件 。
【第二课时】
【学习目标】
1.掌握“SAS”的判定方法。
2.能初步应用“边角边”条件判定两个三角形全等。
3.经历探索三角形全等的过程,体验操作,归纳得出数学结论的过程。
【学习重难点】
1.“边角边”条件的理解和应用。
2.学会分析问题,寻找判定三角形全等的条件。
【学习过程】
一、创设情境。
上节课学习了三角形全等的判定定理边边边,除此之外,判定三角形全等还有没有其他方法?
二、探究指导。
思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能呢?
三、应用新知。
如图:有一池塘,要测池塘两端A,B的距离,可先在平底上取一点C,从点C不经过池塘可以直接到达点A和点B,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE,那么量出DE的长就是A,B的距离,为什么?
四、变式练习。
1.如图,两车从南北方向的路段AB的A端出发,分别向东,向西行进相同的距离,到达C、D两地,此时C、D到B的距离相等吗?为什么?
2.如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,求证∠A=∠D。
3.如图,已知AB=AC,点D、E分别是AB和AC上的点,且DB=EC,求证∠B=∠C。
【第三课时】
【学习目标】
1.掌握“角边角”及“角角边”条件内容。
2.能初步应用“角边角”及“角角边”条件判定两个三角形全等。
3.经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
【学习重难点】
1.“角边角”条件及“角角边”条件。
2.分析问题,寻找判定两个三角形全等的条件。
【学习过程】
一、复习导入。
思考我们已经会哪些条件判定两个三角形全等?
二、探究新知。
思考:师提问,两个角和其中一个角的对边对角相等的两个三角形全等吗?
师出示多媒体:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF(如下图),△ABC和△DEF全等吗?你能用角边角证明得到的结论吗?
生分小组讨论证明,师巡视指导,将一个学生的证明过程展台展示,师生共同纠正,后师生共同总结。
三、应用新知。
如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C。求证:AD=AE。
总结:两角和其中一个角的对边分别相等的两个三角形全等(AAS)。
四、变式练习。
1.要测量池塘两岸相对的两点A、B的距离,在池塘外取AB的垂线BF上的两点C,D,使BC=CD,在画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
2.如图,点D在AB上,点E在AC上,∠B=∠C,那么补充下列哪一个条件后,仍无法判定△ABE≌△ACD?( )
A.AD=AE B.∠AEB=∠ADC
C.BE=CD D.AB=AC
【第四课时】
【学习目标】
1.探索掌握直角三角形全等的条件:“斜边,直角边”。
2.经历探索三角形全等的过程,体验用操作,归纳得出数学结论的过程。
3.充分调动积极性,增强自信心。
【学习重难点】
1.探究直角三角形全等的条件。
2.灵活运用直角三角形全等的条件进行证明。
【学习过程】
一、复习巩固。
我们已经学过了哪些判定三角形全等的方法?
二、情境诱导。
对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?
三、探究新知。
师出示多媒体:任意画一个Rt△ABC,使∠C=90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,把画好的Rt△A′B′C′剪下,放到Rt△ABC上,它们全等吗?
四、应用新知。
如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD。求证:BC=AD。
五、变式练习。
1.如图,C是路段AB的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D、E两地,DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?
2.如图,AB=AD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF,求证:AE=DF。
9 / 9
