第二十四章 圆 单元测试 (含答案)2023—-2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十四章 圆 单元测试 (含答案)2023—-2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 137.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 09:22:54 | ||
图片预览


文档简介
第二十四章 圆
一、单选题
1.已知☉O的半径为5,点P在直线l上,且OP=5,则直线l与☉O的位置关系是( )
A.相切 B.相交 C.相离 D.相切或相交
2.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为( )
A.0个 B.1个 C.2个 D.3个
3.如图,AB是⊙O的直径,⊙O的半径cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
A.cm B.3cm C.2cm D.9cm
4.如图,A、B、C是⊙O上的三个点,∠ABC=25°,则∠AOC的度数是 ( )
A.25° B.65° C.50° D.130°
5.如图,是半圆的直径,、是半圆上的两点,,则( )
A.55° B.65° C.75° D.85°
6.如图,已知AB是⊙O的直径,⊙O的切线CD与AB的延长线交于点D,点C为切点,联接AC,若∠A=26°,则∠D的度数是( )
A.26° B.38° C.42° D.64°
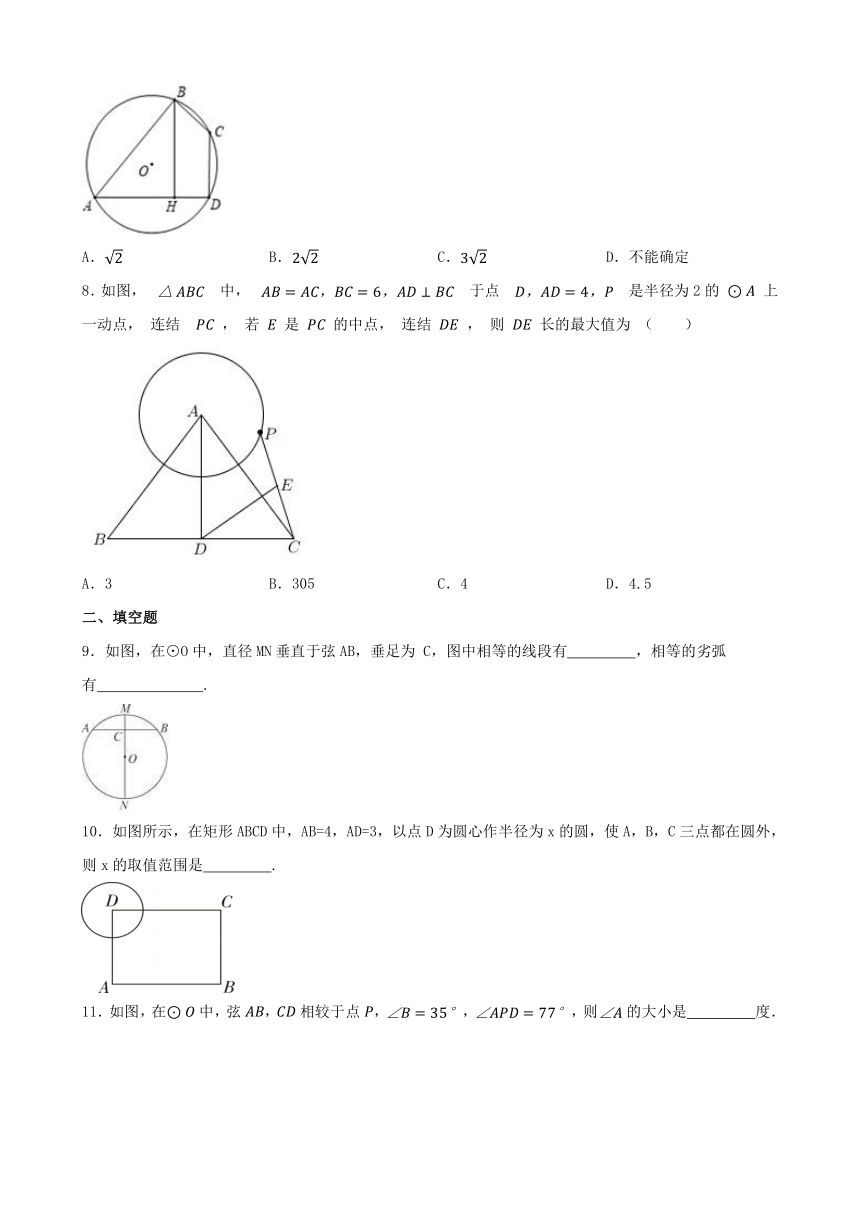
7.如图,四边形 内接于圆 ,过 点作 于点 ,若 , ,则 的长度为( )
A. B. C. D.不能确定
8.如图, 中, 于点 是半径为2的 上一动点, 连结 , 若 是 的中点, 连结 , 则 长的最大值为 ( )
A.3 B.305 C.4 D.4.5
二、填空题
9.如图,在⊙O中,直径MN垂直于弦AB,垂足为 C,图中相等的线段有 ,相等的劣弧有 .
10.如图所示,在矩形ABCD中,AB=4,AD=3,以点D为圆心作半径为x的圆,使A,B,C三点都在圆外,则x的取值范围是 .
11.如图,在中,弦,相较于点,,,则的大小是 度.
12.在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是 (结果不取近似值).
13.已知矩形ABCD,对角线AC与BD相交于点O,AB=6,BC=8,分别以点O、D为圆心画圆,如果⊙O与直线AD相交、与直线CD相离,且⊙D与⊙O内切,那么⊙D的半径长r的取值范围是 .
三、解答题
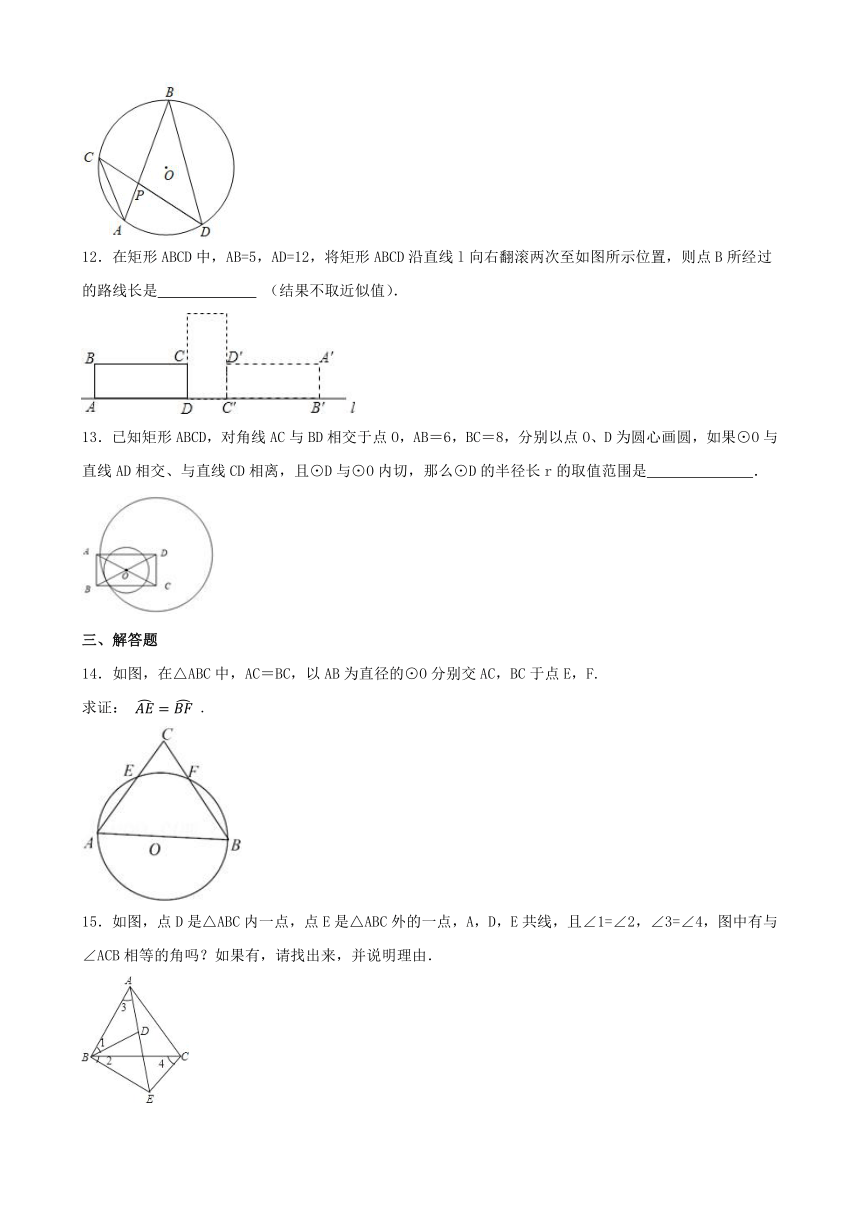
14.如图,在△ABC中,AC=BC,以AB为直径的⊙O分别交AC,BC于点E,F.
求证: .
15.如图,点D是△ABC内一点,点E是△ABC外的一点,A,D,E共线,且∠1=∠2,∠3=∠4,图中有与∠ACB相等的角吗?如果有,请找出来,并说明理由.
16.如图,在△ABC中,∠ACB=90°,AC=BC,O点在△ABC内部,⊙O经过B、C两点且交AB于点D,连接CO并延长交线段AB于点G,以GD、GC为邻边作平行四边形GDEC.
(1)求证:直线DE是⊙O的切线;
(2)若DE=7,CE=5,求⊙O的半径.
17.基本模型:如图1,点A,F,B在同一直线上,若∠A=∠B=∠EFC=90°,易得△AFE~△BCF.
(1)模型拓展:如图2,点A,F,B在同一直线上,若∠A=∠B=∠EFC,求证:△AFE~△BCF;
(2)拓展应用:如图3,AB是半圆⊙O的直径,弦长AC=BC=4 ,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
18.某公园管理人员在巡视公园时,发现有一条圆柱形的输水管道破裂,通知维修人员到场检测,维修员画出水平放置的破裂管道有水部分的截面图(如图).
(1)请你帮忙补全这个输水管道的圆形截面(不写作法,但应保留作图痕迹);
(2)维修员量得这个输水管道有水部分的水面宽AB=12cm,水面最深地方的高度为6cm,请你求出这个圆形截面的半径r及破裂管道有水部分的截面图的面积S.
参考答案
1.D
2.C
3.B
4.C
5.C
6.B
7.B
8.B
9.AC=BC;弧AM=弧BM
10.
11.42
12.12.5π
13.8<r<9.
14.证明:连接BE、AF,如图,
∵AB为直径,
∴∠AEB=∠AFB=90°,
∵CA=CB,
∴∠CAB=∠CBA,
∴∠ABE=∠BAF,
∴ .
15.解:有,∠AEB=∠ACB.理由如下:
∵∠3=∠4,
∴四点A、B、C、E共圆(在一条边的同一侧,该边所对的两个角相等,则四点共圆).
∴∠AEB=∠ACB
16.(1)证明:连接OD,
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∴∠COD=2∠ABC=90°,
∵四边形GDEC是平行四边形,
∴DE∥CG,
∴∠ODE+∠COD=180°,
∴∠ODE=90°,即OD⊥DE,
∵OD是半径,
∴直线DE是⊙O的切线
(2)解:设⊙O的半径为r,
∵四边形GDEC是平行四边形,
∴CG=DE=7,DG=CE=5,
∵∠GOD=90°,
∴OD2+OG2=DG2,即r2+(7﹣r)2=52,
解得:r1=3,r2=4,
当r=3时,OG=4>3,此时点G在⊙O外,不合题意,舍去,
∴r=4,即⊙O的半径4.
17.(1)证明:如图2,∵∠A=∠EFC,
∴∠E+∠EFA=∠EFA+∠CFB,
∴∠E=∠CFB,
∵∠A=∠B,
∴△AFE∽△BCF
(2)解:如图3,∵AB是⊙O的直径,
∴∠ACB=90°,
∴AB= =8,
∵AC=BC,
∴∠A=∠B=45°,
∴∠A=∠B=∠CFE=45°,
由(1)可得△AFE∽△BCF,
∴ ,
即 ,
∴y=﹣ x2+ x(0≤x≤8),
18.解:(1)如图:
(2)过点O作OC⊥AB于D,交弧AB于C,则CD=6cm.
∵OC⊥AB,
∴BD=AD=AB,
∵AB=12cm,
∴BD=AD=6cm,
∵半径为rcm,则OD=(r﹣6)cm,
在Rt△BOD 中,由勾股定理得:
BD2+OD2=BO2,
∴,
解得r=12,
∴这个圆形截面的半径为12cm.
又∵设弧长AB所对圆心角为θ,则,
在Rt△BOD中,BD=6,OB=12,
∴,且∠DOB为Rt△BOD的一个内角,
求得=60°
∴θ=120°
∵S=S扇形OACB面积﹣S△OAB面积=
=(cm2)
一、单选题
1.已知☉O的半径为5,点P在直线l上,且OP=5,则直线l与☉O的位置关系是( )
A.相切 B.相交 C.相离 D.相切或相交
2.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为( )
A.0个 B.1个 C.2个 D.3个
3.如图,AB是⊙O的直径,⊙O的半径cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
A.cm B.3cm C.2cm D.9cm
4.如图,A、B、C是⊙O上的三个点,∠ABC=25°,则∠AOC的度数是 ( )
A.25° B.65° C.50° D.130°
5.如图,是半圆的直径,、是半圆上的两点,,则( )
A.55° B.65° C.75° D.85°
6.如图,已知AB是⊙O的直径,⊙O的切线CD与AB的延长线交于点D,点C为切点,联接AC,若∠A=26°,则∠D的度数是( )
A.26° B.38° C.42° D.64°
7.如图,四边形 内接于圆 ,过 点作 于点 ,若 , ,则 的长度为( )
A. B. C. D.不能确定
8.如图, 中, 于点 是半径为2的 上一动点, 连结 , 若 是 的中点, 连结 , 则 长的最大值为 ( )
A.3 B.305 C.4 D.4.5
二、填空题
9.如图,在⊙O中,直径MN垂直于弦AB,垂足为 C,图中相等的线段有 ,相等的劣弧有 .
10.如图所示,在矩形ABCD中,AB=4,AD=3,以点D为圆心作半径为x的圆,使A,B,C三点都在圆外,则x的取值范围是 .
11.如图,在中,弦,相较于点,,,则的大小是 度.
12.在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是 (结果不取近似值).
13.已知矩形ABCD,对角线AC与BD相交于点O,AB=6,BC=8,分别以点O、D为圆心画圆,如果⊙O与直线AD相交、与直线CD相离,且⊙D与⊙O内切,那么⊙D的半径长r的取值范围是 .
三、解答题
14.如图,在△ABC中,AC=BC,以AB为直径的⊙O分别交AC,BC于点E,F.
求证: .
15.如图,点D是△ABC内一点,点E是△ABC外的一点,A,D,E共线,且∠1=∠2,∠3=∠4,图中有与∠ACB相等的角吗?如果有,请找出来,并说明理由.
16.如图,在△ABC中,∠ACB=90°,AC=BC,O点在△ABC内部,⊙O经过B、C两点且交AB于点D,连接CO并延长交线段AB于点G,以GD、GC为邻边作平行四边形GDEC.
(1)求证:直线DE是⊙O的切线;
(2)若DE=7,CE=5,求⊙O的半径.
17.基本模型:如图1,点A,F,B在同一直线上,若∠A=∠B=∠EFC=90°,易得△AFE~△BCF.
(1)模型拓展:如图2,点A,F,B在同一直线上,若∠A=∠B=∠EFC,求证:△AFE~△BCF;
(2)拓展应用:如图3,AB是半圆⊙O的直径,弦长AC=BC=4 ,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
18.某公园管理人员在巡视公园时,发现有一条圆柱形的输水管道破裂,通知维修人员到场检测,维修员画出水平放置的破裂管道有水部分的截面图(如图).
(1)请你帮忙补全这个输水管道的圆形截面(不写作法,但应保留作图痕迹);
(2)维修员量得这个输水管道有水部分的水面宽AB=12cm,水面最深地方的高度为6cm,请你求出这个圆形截面的半径r及破裂管道有水部分的截面图的面积S.
参考答案
1.D
2.C
3.B
4.C
5.C
6.B
7.B
8.B
9.AC=BC;弧AM=弧BM
10.
11.42
12.12.5π
13.8<r<9.
14.证明:连接BE、AF,如图,
∵AB为直径,
∴∠AEB=∠AFB=90°,
∵CA=CB,
∴∠CAB=∠CBA,
∴∠ABE=∠BAF,
∴ .
15.解:有,∠AEB=∠ACB.理由如下:
∵∠3=∠4,
∴四点A、B、C、E共圆(在一条边的同一侧,该边所对的两个角相等,则四点共圆).
∴∠AEB=∠ACB
16.(1)证明:连接OD,
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∴∠COD=2∠ABC=90°,
∵四边形GDEC是平行四边形,
∴DE∥CG,
∴∠ODE+∠COD=180°,
∴∠ODE=90°,即OD⊥DE,
∵OD是半径,
∴直线DE是⊙O的切线
(2)解:设⊙O的半径为r,
∵四边形GDEC是平行四边形,
∴CG=DE=7,DG=CE=5,
∵∠GOD=90°,
∴OD2+OG2=DG2,即r2+(7﹣r)2=52,
解得:r1=3,r2=4,
当r=3时,OG=4>3,此时点G在⊙O外,不合题意,舍去,
∴r=4,即⊙O的半径4.
17.(1)证明:如图2,∵∠A=∠EFC,
∴∠E+∠EFA=∠EFA+∠CFB,
∴∠E=∠CFB,
∵∠A=∠B,
∴△AFE∽△BCF
(2)解:如图3,∵AB是⊙O的直径,
∴∠ACB=90°,
∴AB= =8,
∵AC=BC,
∴∠A=∠B=45°,
∴∠A=∠B=∠CFE=45°,
由(1)可得△AFE∽△BCF,
∴ ,
即 ,
∴y=﹣ x2+ x(0≤x≤8),
18.解:(1)如图:
(2)过点O作OC⊥AB于D,交弧AB于C,则CD=6cm.
∵OC⊥AB,
∴BD=AD=AB,
∵AB=12cm,
∴BD=AD=6cm,
∵半径为rcm,则OD=(r﹣6)cm,
在Rt△BOD 中,由勾股定理得:
BD2+OD2=BO2,
∴,
解得r=12,
∴这个圆形截面的半径为12cm.
又∵设弧长AB所对圆心角为θ,则,
在Rt△BOD中,BD=6,OB=12,
∴,且∠DOB为Rt△BOD的一个内角,
求得=60°
∴θ=120°
∵S=S扇形OACB面积﹣S△OAB面积=
=(cm2)
同课章节目录
