27.1 图形的相似 课件(共33张PPT)
文档属性
| 名称 | 27.1 图形的相似 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
人教九上数学同步精品课件
人教版九年级上册
27.1 图形的相似
第二十七章 相似
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 了解相似图形和相似比的概念,会计算比例线段.
2. 理解相似多边形的定义.
3. 能根据多边形相似进行相关的计算,会根据条件判断两个多边形是否相似.
重点
难点
学习目标
两张图片有何关系?
两两之间形状相同大小不同
新课引入
我们能发现上述图片两两之间形状相同大小不同,于是我们把这类形状相同大小不同图形叫做相似图形,其中一个图形可以看作由另一个图形放大或缩小得到.
新知学习
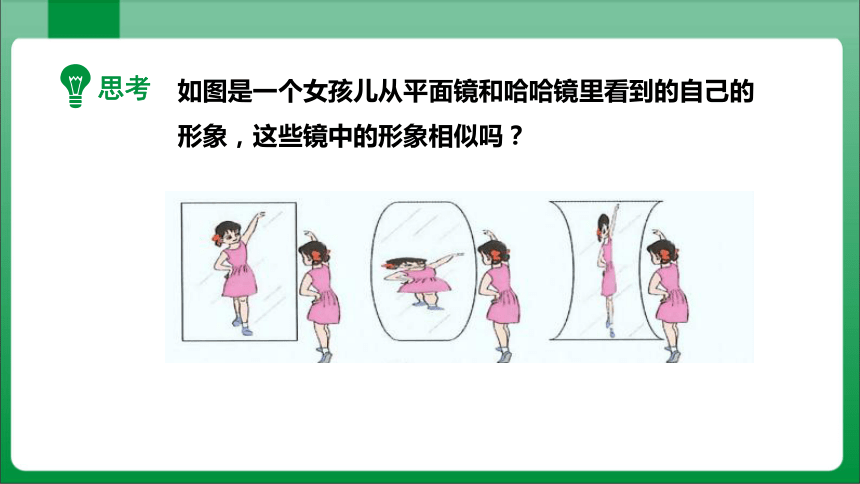
思考
如图是一个女孩儿从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象相似吗?
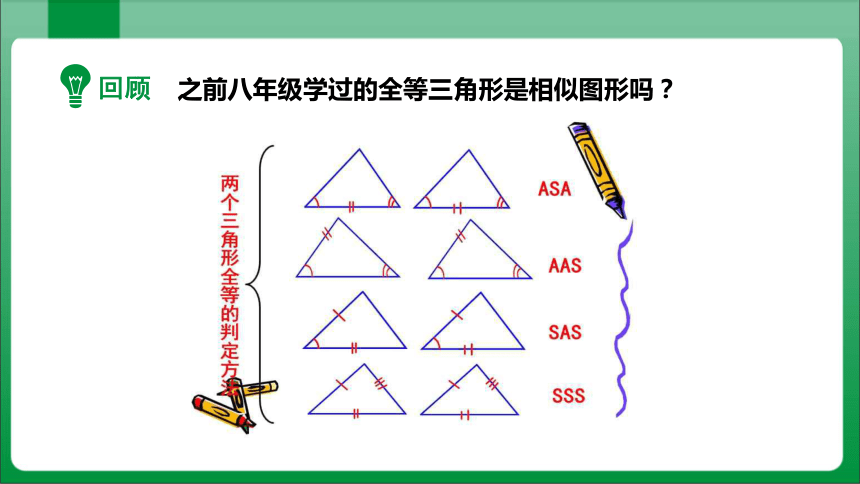
之前八年级学过的全等三角形是相似图形吗?
回顾
1.“形状相同”是判定相似图形的唯一条件.
2.两个图形相似是指它们的形状相同,与它们的位置、大小无关.
3.全等图形是一种特殊的相似图形,不仅形状相同,大小也相同.
归纳总结
1.如图,从放大镜里看到的三角尺和原来的三角尺相似吗
针对训练
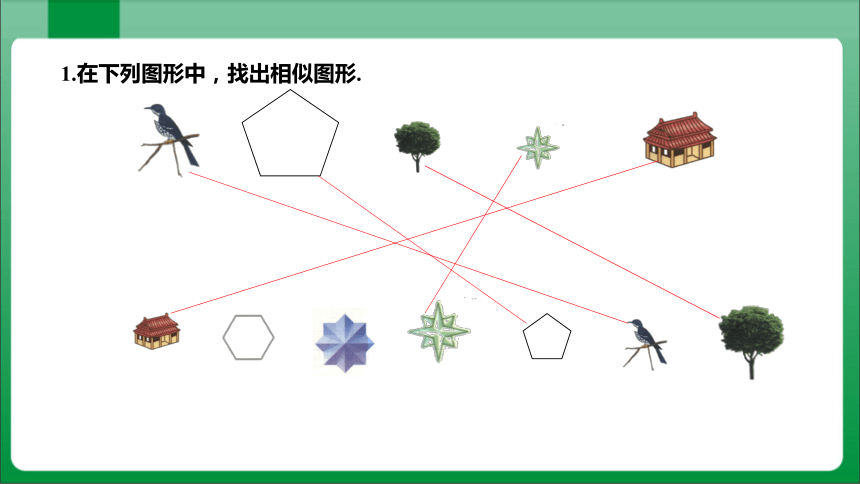
1.在下列图形中,找出相似图形.
这两条线段的长度分别是多少?它们的比是多少
二 比例线段
思考
A B
C D
线段的比:在同一长度单位下,量得的两条线段长度的比叫做这两条线段的比.
注意:线段的比是两条线段的长度比,所以要求两条线段的长度单位必须一致
新知学习
第11~13张PPT放在第29张PPT后面
四条线段成比例
探究
a
c
b
d
量出a,b,c,d的长度,并观察它们有何比例关系?
四条线段成比例:对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等.如(即 ad = bc).我们就说这四条线段成比例.
新知学习
1.下列各组中的四条线段成比例的是( )
针对训练
A. a= ,b=3,c=4,d=
B. a=4 ,b=6,c=4,d=10
C. a=4 ,b= ,c= ,d=
D. a=2,b=3,c=4,d=1
C
3
4
甲
4
8
丙
3
6
乙
下面甲、乙、丙三个矩形相似吗?
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的对应边的比叫作相似比.
不相似
所有矩形都相似吗?为什么?
不一定相似.因为虽然它们对应角相等,但它们对应边不一定成比例.
思考
矩形
所有菱形都相似吗?为什么?
不一定相似.因为虽然它们对应边是成比例的,但它们的对应角不一定相等.
菱形
所有等边三角形都相似吗?为什么?
相似,等边三角形的每个角都为60°, 三边都相等. 所以满足对应角相等,以及对应边的比相等.
所有正方形都相似吗?为什么?所有正多边形呢?
相似,正方形的每个角都为90°,四边都相等. 所以满足对应角相等,以及对应边的比相等.
任意两个边数相等的正多边形都相似.
①对应角相等
②对应边的比相等,
那么这两个多边形是相似多边形.
相似多边形的判定方法
归纳总结
相似多边形的对应边的比叫作相似比.
例 如图,四边形 ABCD 和 EFGH 相似,求角 α,β 的大小和 EH 的长度 x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
在四边形 ABCD 中,
β = 360°-(78°+83°+118°) = 81°.
∠α = ∠C = 83°,∠A = ∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,
∴ 它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
∵ 四边形 ABCD 和四边形 EFGH 相似,
∴它们的对应边成比例,由此可得
解得 x = 28 cm.
,即 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
针对训练
1.如图所示的两个五边形相似,求未知边 a,b, c,d 的长度.
5
3
2
c
d
7.5
b
a
6
9
解:相似多边形的对应边的成比例,由此可得
解得:a = 3,b = 4.5,c = 4,d = 6.
所以未知边 a,b,c,d 的长度分别为3,4.5,4,6.
, , , ,
2.一块长3m、宽1.5m的矩形黑板如图所示,镶在其外围的木板边框宽7.5cm,边框的内外边缘所成的矩形相似吗?为什么?
两个矩形满足各角分别相等
两个矩形的各边不成比例,不相似.
各边比值为
(1)
2
3
3
4.5
2
3
2.5
6
(2)
3.图中每组的两个矩形相似吗?说说你的理由
第(1)组两个矩形满足各角分别相等,且 ,各边成比例,相似
第(2)组两个矩形满足各角分别相等, ,各边不成比例,不相似
1.两个相似多边形的相似比是3:7,其中一个多边形的最长边是21 ,则另一个多边形的最长边是_______.
解析:设另一个多边形最长边为x,
①当x是较大的多边形的边,
∴ ,x=49.
②当x是较小的多边形的边: ,x=9,
∴x=49或9.
随堂练习
49或9
不确定所在多边形是较大的还是较小的,所以要分类讨论
2.如图,梯形ABCD中,AB//CD,对角线AC、BD交于点O,过点O作EF//AB,分别交AD、BC 于 E、F,求证:
(1)OE=OF
证:∵EF//DC,
∴
∵AB//DC,
∴
∴OE=OF.
(2)
证:∵EF//AB,∴
∵EF//DC,∴
∴
∵OE=OF= EF
∴
即
图形的相似
相似图形
相似多边形
形状相同的图形叫做相似图形
对应角相等,对应边成比例
相似多边形对应边
的比叫做相似比
全等图形是相似比为1的相似图形
相似图形的大小不一定相同
课堂小结
2.已知a,b,c为△ABC的三边,且 ,则k的值为____.
1
解析:∵ ,
∴2a=(b+c)k=bk+ck①,2b=(a+c)k=ak+ck②, 2c=(a+b)k=ak+bk③,
①+②+③,整理得2(a+b+c)=2k(a +b+c),
再根据a、b、c为△ABC的三边可得,a+b+c≠ 0,
∴2k=2,∴k=1.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
27.1 图形的相似
第二十七章 相似
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 了解相似图形和相似比的概念,会计算比例线段.
2. 理解相似多边形的定义.
3. 能根据多边形相似进行相关的计算,会根据条件判断两个多边形是否相似.
重点
难点
学习目标
两张图片有何关系?
两两之间形状相同大小不同
新课引入
我们能发现上述图片两两之间形状相同大小不同,于是我们把这类形状相同大小不同图形叫做相似图形,其中一个图形可以看作由另一个图形放大或缩小得到.
新知学习
思考
如图是一个女孩儿从平面镜和哈哈镜里看到的自己的形象,这些镜中的形象相似吗?
之前八年级学过的全等三角形是相似图形吗?
回顾
1.“形状相同”是判定相似图形的唯一条件.
2.两个图形相似是指它们的形状相同,与它们的位置、大小无关.
3.全等图形是一种特殊的相似图形,不仅形状相同,大小也相同.
归纳总结
1.如图,从放大镜里看到的三角尺和原来的三角尺相似吗
针对训练
1.在下列图形中,找出相似图形.
这两条线段的长度分别是多少?它们的比是多少
二 比例线段
思考
A B
C D
线段的比:在同一长度单位下,量得的两条线段长度的比叫做这两条线段的比.
注意:线段的比是两条线段的长度比,所以要求两条线段的长度单位必须一致
新知学习
第11~13张PPT放在第29张PPT后面
四条线段成比例
探究
a
c
b
d
量出a,b,c,d的长度,并观察它们有何比例关系?
四条线段成比例:对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等.如(即 ad = bc).我们就说这四条线段成比例.
新知学习
1.下列各组中的四条线段成比例的是( )
针对训练
A. a= ,b=3,c=4,d=
B. a=4 ,b=6,c=4,d=10
C. a=4 ,b= ,c= ,d=
D. a=2,b=3,c=4,d=1
C
3
4
甲
4
8
丙
3
6
乙
下面甲、乙、丙三个矩形相似吗?
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的对应边的比叫作相似比.
不相似
所有矩形都相似吗?为什么?
不一定相似.因为虽然它们对应角相等,但它们对应边不一定成比例.
思考
矩形
所有菱形都相似吗?为什么?
不一定相似.因为虽然它们对应边是成比例的,但它们的对应角不一定相等.
菱形
所有等边三角形都相似吗?为什么?
相似,等边三角形的每个角都为60°, 三边都相等. 所以满足对应角相等,以及对应边的比相等.
所有正方形都相似吗?为什么?所有正多边形呢?
相似,正方形的每个角都为90°,四边都相等. 所以满足对应角相等,以及对应边的比相等.
任意两个边数相等的正多边形都相似.
①对应角相等
②对应边的比相等,
那么这两个多边形是相似多边形.
相似多边形的判定方法
归纳总结
相似多边形的对应边的比叫作相似比.
例 如图,四边形 ABCD 和 EFGH 相似,求角 α,β 的大小和 EH 的长度 x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
在四边形 ABCD 中,
β = 360°-(78°+83°+118°) = 81°.
∠α = ∠C = 83°,∠A = ∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,
∴ 它们的对应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
∵ 四边形 ABCD 和四边形 EFGH 相似,
∴它们的对应边成比例,由此可得
解得 x = 28 cm.
,即 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
针对训练
1.如图所示的两个五边形相似,求未知边 a,b, c,d 的长度.
5
3
2
c
d
7.5
b
a
6
9
解:相似多边形的对应边的成比例,由此可得
解得:a = 3,b = 4.5,c = 4,d = 6.
所以未知边 a,b,c,d 的长度分别为3,4.5,4,6.
, , , ,
2.一块长3m、宽1.5m的矩形黑板如图所示,镶在其外围的木板边框宽7.5cm,边框的内外边缘所成的矩形相似吗?为什么?
两个矩形满足各角分别相等
两个矩形的各边不成比例,不相似.
各边比值为
(1)
2
3
3
4.5
2
3
2.5
6
(2)
3.图中每组的两个矩形相似吗?说说你的理由
第(1)组两个矩形满足各角分别相等,且 ,各边成比例,相似
第(2)组两个矩形满足各角分别相等, ,各边不成比例,不相似
1.两个相似多边形的相似比是3:7,其中一个多边形的最长边是21 ,则另一个多边形的最长边是_______.
解析:设另一个多边形最长边为x,
①当x是较大的多边形的边,
∴ ,x=49.
②当x是较小的多边形的边: ,x=9,
∴x=49或9.
随堂练习
49或9
不确定所在多边形是较大的还是较小的,所以要分类讨论
2.如图,梯形ABCD中,AB//CD,对角线AC、BD交于点O,过点O作EF//AB,分别交AD、BC 于 E、F,求证:
(1)OE=OF
证:∵EF//DC,
∴
∵AB//DC,
∴
∴OE=OF.
(2)
证:∵EF//AB,∴
∵EF//DC,∴
∴
∵OE=OF= EF
∴
即
图形的相似
相似图形
相似多边形
形状相同的图形叫做相似图形
对应角相等,对应边成比例
相似多边形对应边
的比叫做相似比
全等图形是相似比为1的相似图形
相似图形的大小不一定相同
课堂小结
2.已知a,b,c为△ABC的三边,且 ,则k的值为____.
1
解析:∵ ,
∴2a=(b+c)k=bk+ck①,2b=(a+c)k=ak+ck②, 2c=(a+b)k=ak+bk③,
①+②+③,整理得2(a+b+c)=2k(a +b+c),
再根据a、b、c为△ABC的三边可得,a+b+c≠ 0,
∴2k=2,∴k=1.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
