27.2.3 两角相等判定 课件(共32张PPT)
文档属性
| 名称 | 27.2.3 两角相等判定 课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 21.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 21:14:33 | ||
图片预览








文档简介
(共32张PPT)
人教九上数学同步精品课件
人教版九年级上册
27.2.3 两角相等判定
第二十七章 相似
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 探索两角分别相等的两个三角形相似的判定定理.
2. 掌握利用两角来判定两个三角形相似的方法,并能进行相关计算.
3. 掌握判定两个直角三角形相似的方法,并能进行相关计算.
重点
难点
学习目标
探究
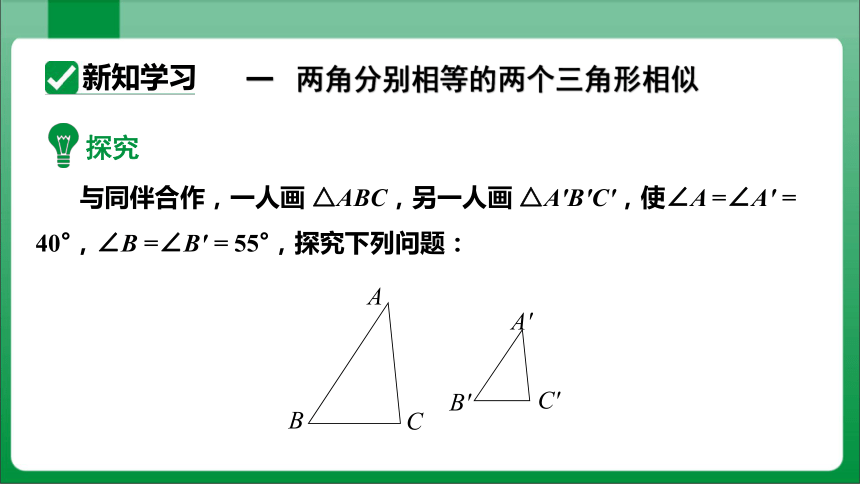
一 两角分别相等的两个三角形相似
C
A
B
A'
B'
C'
与同伴合作,一人画 △ABC,另一人画 △A′B′C′,使∠A =∠A′ = 40°,∠B =∠B′ = 55°,探究下列问题:
新知学习
上节课我们学习了有哪些判定三角形相似的方法?
三边成比例的两个三角形相似.
两边成比例且夹角相等的两个三角形相似.
新课引入
下来我们探究一下证明两个三角形相似的新方法
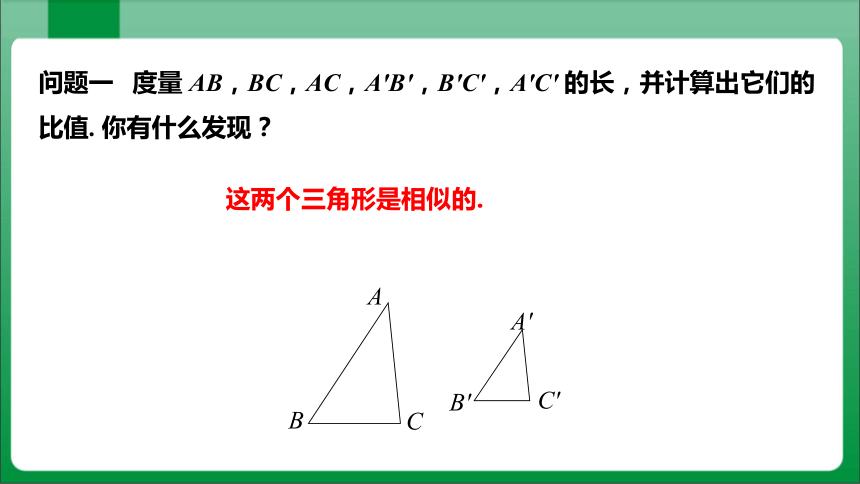
问题一 度量 AB,BC,AC,A′B′,B′C′,A′C′ 的长,并计算出它们的比值. 你有什么发现?
这两个三角形是相似的.
C
A
B
A'
B'
C'
又∵ A′D = AB,∠A =∠A′,
∴△A′DE ≌ △ABC,
∴△ABC ∽ △A′B′C′ .
问题二 试证明△ABC∽△A′B′C′.
C
A
A'
B
B'
C'
D
E
证明:在 △A′B′C′ 的边 A′B′(或 A′B′ 的延长线)上,截取 A′D = AB,过点 D 作 DE // B′C′,交 A′C′ 于点 E,则有 △A′DE ∽ △A′B′C′,∠A′DE =∠B′.
∵∠B =∠B′,
∴∠A′DE =∠B.
归纳
由此得到利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
符号语言:
C
A
B
A'
B'
C'
∴
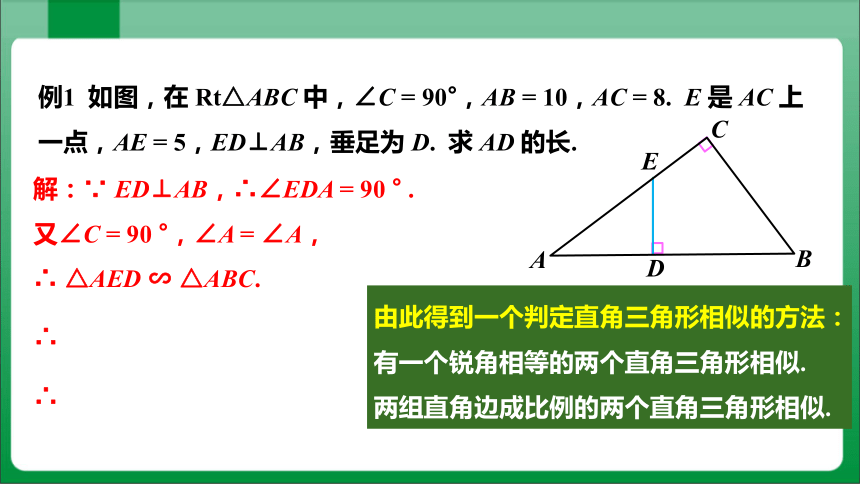
解:∵ ED⊥AB,∴∠EDA = 90 ° .
又∠C = 90 °,∠A = ∠A,
∴ △AED ∽ △ABC.
例1 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为 D. 求 AD 的长.
D
A
B
C
E
∴
由此得到一个判定直角三角形相似的方法:
有一个锐角相等的两个直角三角形相似.
两组直角边成比例的两个直角三角形相似.
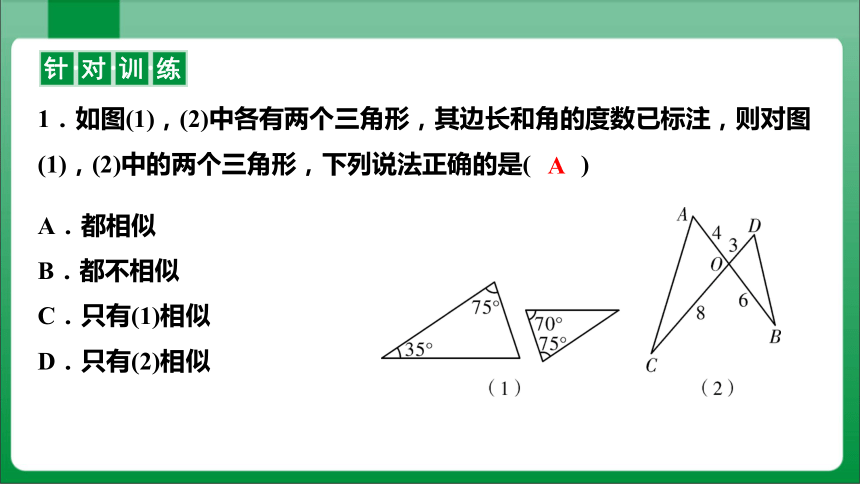
1.如图(1),(2)中各有两个三角形,其边长和角的度数已标注,则对图(1),(2)中的两个三角形,下列说法正确的是( )
针对训练
A.都相似
B.都不相似
C.只有(1)相似
D.只有(2)相似
A
证明:∵ 在 △ ABC 中,∠A = 40 ° ,∠B = 80 ° ,
∴ ∠C = 180 °-∠A-∠B = 60 °.
∵ 在 △DEF 中,∠E = 80 °,∠F = 60 °.
∴ ∠B = ∠E,∠C = ∠F.
∴ △ABC ∽ △DEF.
2.如图,在△ABC 和 △DEF 中,∠A = 40°,∠B = 80°,∠E = 80 °,∠F = 60 °.求证:△ABC ∽△DEF.
A
C
B
F
E
D
3.如图,点E、F分别在矩形ABCD的边DC、BC上,∠AEF=90°,∠AFB=2∠ DAE=72°,则图中甲、乙、丙三个三角形中相似的是( ).
A.只有甲与乙 B.只有乙与丙
C.只有甲与丙 D.甲与乙与丙
D
解:∵∠ AFB=72°
∴∠BAF=18°,∠EAF=90° -∠BAF-∠ DAE=36°
∴∠DAE=∠EAF=∠CEF
∵∠ADE=∠AEF=∠ECF
∴△DAE∽△EAF∽△CEF,故选D
证明:∵CD为Rt△ABC斜边上的中线
∴CD=AD,∠ACD=∠A
∵DE//AC
∴∠ ACD=∠CDE,∠A=∠CDE
∵∠ACB=90°,CE⊥CD
∴∠ACB=∠DCE
∴△ABC∽△ DEC
4.如图,已知CD为Rt△ABC斜边上的中线,过点D作AC的平行线,过点C作CD的垂线,两线相交于点E.求证:△ABC∽△ DEC.
5.如图,在△ABC中,∠ACD=∠B,若AD=2,BD=3,则AC的长为( ).
A. B. C. D.6
A
解:在△ADC和△ ACB中
∵∠ACD=∠ B,∠A=∠A
∴△ADC∽△ACB,AC:AB=AD:AC
∴
∵AD=2,AB=AD+BD=2+3=5
∴AC =5×2=10
∴AC=
思考
对于两个直角三角形,我们还可以用 “HL”判定它们全等. 那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
二 判定两个直角三角形相似
例2 如图,在 Rt△ABC 和 Rt△A′B′C′ 中,∠C=90°,∠C′=90°,
求证:Rt△ABC ∽ Rt△A′B′C′.
C
A
A'
B
B'
C'
分析:要证 Rt△ABC ∽ Rt△A′B′C′ ,
可设法证
若设
则只需证
∴
∴
C
A
A'
B
B'
C'
∴ Rt△ABC ∽ Rt△A′B′C′.
证明:设 = k ,则 AB = kA′B′,AC = kA′C′.
由勾股定理,得
由此得到另一个判定直角三角形相似的方法:
斜边和一直角边成比例的两个直角三角形相似.
1.如图,Rt△ABC 中,CD 是斜边 AB 上的高.
求证:(1)△ACD ∽ △ABC;
证明:(1)∵CD 是斜边 AB 上的高,∴∠ADC = 90°.
又∵∠A = ∠A,∴△ACD ∽ △ABC.
在 Rt△ABC 中,∠ACB = 90°,
∴∠ADC = ∠ACB.
A
B
C
D
∟
针对训练
证明:(2)∵CD 是斜边 AB 上的高,
∴∠CDB = 90°.
求证: (2)△CBD ∽ △ABC.
又∵∠B = ∠B,∴△CBD ∽ △ABC.
在 Rt△ABC 中,∠ACB = 90°,
∴∠CDB = ∠ACB.
A
B
C
D
∟
2. 如图,在 Rt△ABC 中, ∠ABC = 90°,BD⊥AC于D. 若 AB=6,AD=2,则 BD= ,AC= ,BC= .
18
D
B
C
A
∟
证明: ∵ △ABC 的高AD、BE交于点F,
∴ ∠FEA=∠FDB=90°,
∠AFE =∠BFD (对顶角相等).
∴ △FEA ∽ △ FDB,
∴
3. 如图,△ABC 的高 AD,BE 交于点 F.求证:
D
C
A
B
E
F
判定两三角形相似的思路:
(1)平行于三角形一边的直线,找两个三角形;
(2)已知一角对应相等,找另一角对应相等,或夹这个角的两边成比例;
(3)已知两边对应成比例,找夹角相等,或与第三边成比例;
(4)已知等腰三角形,找顶角相等,或底角相等,或底、腰对应成比例.
(5)已知直角三角形,找一组锐角相等,或两直角边对应成比例,或斜边、一直角边对应成比例.
归纳
1.如图,在边长为 4 的正方形 ABCD 中,P 是边 BC 上的一点 QP⊥AP 交 DC 于点 Q,设 BP =x,△ADQ 的面积为 y.
(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围;
解:(1)∵四边形 ABCD 是正方形
∴∠B=∠C=90°, ∠BAP +∠APB =90°.
∵ QP⊥AP
∴∠QPC +∠APB =90°, ∠BAP =∠QPC,
∴△ABP ∽△PCQ
∴ ,即 ,
∴ (0随堂练习
(2)点 P 在何位置时,△ADQ 的面积最小?最小面积是多少?
解:(2) ∵
∴当 x =2 时,y 最小,且最小值为6
即当点 P 是 BC 的中点时
△ADQ 的面积最小,最小面积为6
2.如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥ AM,垂足为F,交AD的延长线于点E,交DC于点N.
证明: ∵四边形ABCD是正方形
∴AB=AD,∠ B=90°,AD//BC
∴∠ AMB=∠ EAF
∵EF⊥AM
∴∠AFE=90°,∠B=∠AFE
∴△ABM∽△EFA
(1)求证:△ABM∽△EFA
(2)若AB=12,BM=5,求DE的长.
解: ∵∠B=90°,AB=12,BM=5
∴AM= ,AD=12
∵F是AM的中点
∴
∵△ABM∽△ EFA
∴ ,即 ,AE=16.9
∴DE=AE-AD=4.9
3.(武汉中考节选)已知 AB 是⊙O 的直径,AM 和 BN 是⊙O 的两条切线,DC 与⊙O 相切于点 E,分别交 AM,BN 于D,C 两点,如图.求证:AB2 =4AD·BC.
证明:如图,连接 OC,OD
∵ AM 和 BN 是⊙O 的两条切线
∴ AM⊥AB, BN⊥AB, AM//BN, ∠ADE +∠BCE = 180°
∵ DC 切⊙O 于点E
∴∠DOC =90°,∠AOD +∠COB = 90°
∵∠AOD+∠ADO =90°
∴ ∠ADO =∠COB
∵∠OAD =∠OBC =90°
∴△AOD∽△BCO,
∵ OA =OB = AB
∴ ,即 AB =4AD·BC
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
27.2.3 两角相等判定
第二十七章 相似
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 探索两角分别相等的两个三角形相似的判定定理.
2. 掌握利用两角来判定两个三角形相似的方法,并能进行相关计算.
3. 掌握判定两个直角三角形相似的方法,并能进行相关计算.
重点
难点
学习目标
探究
一 两角分别相等的两个三角形相似
C
A
B
A'
B'
C'
与同伴合作,一人画 △ABC,另一人画 △A′B′C′,使∠A =∠A′ = 40°,∠B =∠B′ = 55°,探究下列问题:
新知学习
上节课我们学习了有哪些判定三角形相似的方法?
三边成比例的两个三角形相似.
两边成比例且夹角相等的两个三角形相似.
新课引入
下来我们探究一下证明两个三角形相似的新方法
问题一 度量 AB,BC,AC,A′B′,B′C′,A′C′ 的长,并计算出它们的比值. 你有什么发现?
这两个三角形是相似的.
C
A
B
A'
B'
C'
又∵ A′D = AB,∠A =∠A′,
∴△A′DE ≌ △ABC,
∴△ABC ∽ △A′B′C′ .
问题二 试证明△ABC∽△A′B′C′.
C
A
A'
B
B'
C'
D
E
证明:在 △A′B′C′ 的边 A′B′(或 A′B′ 的延长线)上,截取 A′D = AB,过点 D 作 DE // B′C′,交 A′C′ 于点 E,则有 △A′DE ∽ △A′B′C′,∠A′DE =∠B′.
∵∠B =∠B′,
∴∠A′DE =∠B.
归纳
由此得到利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
符号语言:
C
A
B
A'
B'
C'
∴
解:∵ ED⊥AB,∴∠EDA = 90 ° .
又∠C = 90 °,∠A = ∠A,
∴ △AED ∽ △ABC.
例1 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为 D. 求 AD 的长.
D
A
B
C
E
∴
由此得到一个判定直角三角形相似的方法:
有一个锐角相等的两个直角三角形相似.
两组直角边成比例的两个直角三角形相似.
1.如图(1),(2)中各有两个三角形,其边长和角的度数已标注,则对图(1),(2)中的两个三角形,下列说法正确的是( )
针对训练
A.都相似
B.都不相似
C.只有(1)相似
D.只有(2)相似
A
证明:∵ 在 △ ABC 中,∠A = 40 ° ,∠B = 80 ° ,
∴ ∠C = 180 °-∠A-∠B = 60 °.
∵ 在 △DEF 中,∠E = 80 °,∠F = 60 °.
∴ ∠B = ∠E,∠C = ∠F.
∴ △ABC ∽ △DEF.
2.如图,在△ABC 和 △DEF 中,∠A = 40°,∠B = 80°,∠E = 80 °,∠F = 60 °.求证:△ABC ∽△DEF.
A
C
B
F
E
D
3.如图,点E、F分别在矩形ABCD的边DC、BC上,∠AEF=90°,∠AFB=2∠ DAE=72°,则图中甲、乙、丙三个三角形中相似的是( ).
A.只有甲与乙 B.只有乙与丙
C.只有甲与丙 D.甲与乙与丙
D
解:∵∠ AFB=72°
∴∠BAF=18°,∠EAF=90° -∠BAF-∠ DAE=36°
∴∠DAE=∠EAF=∠CEF
∵∠ADE=∠AEF=∠ECF
∴△DAE∽△EAF∽△CEF,故选D
证明:∵CD为Rt△ABC斜边上的中线
∴CD=AD,∠ACD=∠A
∵DE//AC
∴∠ ACD=∠CDE,∠A=∠CDE
∵∠ACB=90°,CE⊥CD
∴∠ACB=∠DCE
∴△ABC∽△ DEC
4.如图,已知CD为Rt△ABC斜边上的中线,过点D作AC的平行线,过点C作CD的垂线,两线相交于点E.求证:△ABC∽△ DEC.
5.如图,在△ABC中,∠ACD=∠B,若AD=2,BD=3,则AC的长为( ).
A. B. C. D.6
A
解:在△ADC和△ ACB中
∵∠ACD=∠ B,∠A=∠A
∴△ADC∽△ACB,AC:AB=AD:AC
∴
∵AD=2,AB=AD+BD=2+3=5
∴AC =5×2=10
∴AC=
思考
对于两个直角三角形,我们还可以用 “HL”判定它们全等. 那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
二 判定两个直角三角形相似
例2 如图,在 Rt△ABC 和 Rt△A′B′C′ 中,∠C=90°,∠C′=90°,
求证:Rt△ABC ∽ Rt△A′B′C′.
C
A
A'
B
B'
C'
分析:要证 Rt△ABC ∽ Rt△A′B′C′ ,
可设法证
若设
则只需证
∴
∴
C
A
A'
B
B'
C'
∴ Rt△ABC ∽ Rt△A′B′C′.
证明:设 = k ,则 AB = kA′B′,AC = kA′C′.
由勾股定理,得
由此得到另一个判定直角三角形相似的方法:
斜边和一直角边成比例的两个直角三角形相似.
1.如图,Rt△ABC 中,CD 是斜边 AB 上的高.
求证:(1)△ACD ∽ △ABC;
证明:(1)∵CD 是斜边 AB 上的高,∴∠ADC = 90°.
又∵∠A = ∠A,∴△ACD ∽ △ABC.
在 Rt△ABC 中,∠ACB = 90°,
∴∠ADC = ∠ACB.
A
B
C
D
∟
针对训练
证明:(2)∵CD 是斜边 AB 上的高,
∴∠CDB = 90°.
求证: (2)△CBD ∽ △ABC.
又∵∠B = ∠B,∴△CBD ∽ △ABC.
在 Rt△ABC 中,∠ACB = 90°,
∴∠CDB = ∠ACB.
A
B
C
D
∟
2. 如图,在 Rt△ABC 中, ∠ABC = 90°,BD⊥AC于D. 若 AB=6,AD=2,则 BD= ,AC= ,BC= .
18
D
B
C
A
∟
证明: ∵ △ABC 的高AD、BE交于点F,
∴ ∠FEA=∠FDB=90°,
∠AFE =∠BFD (对顶角相等).
∴ △FEA ∽ △ FDB,
∴
3. 如图,△ABC 的高 AD,BE 交于点 F.求证:
D
C
A
B
E
F
判定两三角形相似的思路:
(1)平行于三角形一边的直线,找两个三角形;
(2)已知一角对应相等,找另一角对应相等,或夹这个角的两边成比例;
(3)已知两边对应成比例,找夹角相等,或与第三边成比例;
(4)已知等腰三角形,找顶角相等,或底角相等,或底、腰对应成比例.
(5)已知直角三角形,找一组锐角相等,或两直角边对应成比例,或斜边、一直角边对应成比例.
归纳
1.如图,在边长为 4 的正方形 ABCD 中,P 是边 BC 上的一点 QP⊥AP 交 DC 于点 Q,设 BP =x,△ADQ 的面积为 y.
(1)求 y 与 x 之间的函数关系式,并写出自变量 x 的取值范围;
解:(1)∵四边形 ABCD 是正方形
∴∠B=∠C=90°, ∠BAP +∠APB =90°.
∵ QP⊥AP
∴∠QPC +∠APB =90°, ∠BAP =∠QPC,
∴△ABP ∽△PCQ
∴ ,即 ,
∴ (0
(2)点 P 在何位置时,△ADQ 的面积最小?最小面积是多少?
解:(2) ∵
∴当 x =2 时,y 最小,且最小值为6
即当点 P 是 BC 的中点时
△ADQ 的面积最小,最小面积为6
2.如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥ AM,垂足为F,交AD的延长线于点E,交DC于点N.
证明: ∵四边形ABCD是正方形
∴AB=AD,∠ B=90°,AD//BC
∴∠ AMB=∠ EAF
∵EF⊥AM
∴∠AFE=90°,∠B=∠AFE
∴△ABM∽△EFA
(1)求证:△ABM∽△EFA
(2)若AB=12,BM=5,求DE的长.
解: ∵∠B=90°,AB=12,BM=5
∴AM= ,AD=12
∵F是AM的中点
∴
∵△ABM∽△ EFA
∴ ,即 ,AE=16.9
∴DE=AE-AD=4.9
3.(武汉中考节选)已知 AB 是⊙O 的直径,AM 和 BN 是⊙O 的两条切线,DC 与⊙O 相切于点 E,分别交 AM,BN 于D,C 两点,如图.求证:AB2 =4AD·BC.
证明:如图,连接 OC,OD
∵ AM 和 BN 是⊙O 的两条切线
∴ AM⊥AB, BN⊥AB, AM//BN, ∠ADE +∠BCE = 180°
∵ DC 切⊙O 于点E
∴∠DOC =90°,∠AOD +∠COB = 90°
∵∠AOD+∠ADO =90°
∴ ∠ADO =∠COB
∵∠OAD =∠OBC =90°
∴△AOD∽△BCO,
∵ OA =OB = AB
∴ ,即 AB =4AD·BC
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
