27.2.4 相似三角形的性质 课件(共29张PPT)
文档属性
| 名称 | 27.2.4 相似三角形的性质 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 21.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 21:19:30 | ||
图片预览







文档简介
(共29张PPT)
人教九上数学同步精品课件
人教版九年级上册
27.2.4 相似三角形的性质
第二十七章 相似
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 理解并掌握相似三角形中对应线段的比等于相似比,并运用其解决问题.
2. 理解相似三角形面积的比等于相似比的平方,并运用其解决问题.
学习目标
重点
难点
1. 相似三角形的判定方法有哪几种?
①定义:对应边成比例,对应角相等的两个三角形相似;
②平行于三角形一边的直线与另外两边相交所构成的三角形与原三角形相似;
③三边成比例的两个三角形相似;
④两边成比例且夹角相等的两个三角形相似;
⑤两角分别相等的两个三角形相似;
⑥一组直角边和斜边成比例的两个直角三角形相似.
新课引入
2. 三角形中有各种各样的几何量,例如三条边的长度,三个内角的度数,高、中线、角平分线的长度,以及周长、面积等.如果两个三角形相似,那么它们的这些几何量之间有什么关系呢?
让我们一起来探究吧!
探究
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
新知学习
A
B
C
A'
B'
C'
D'
D
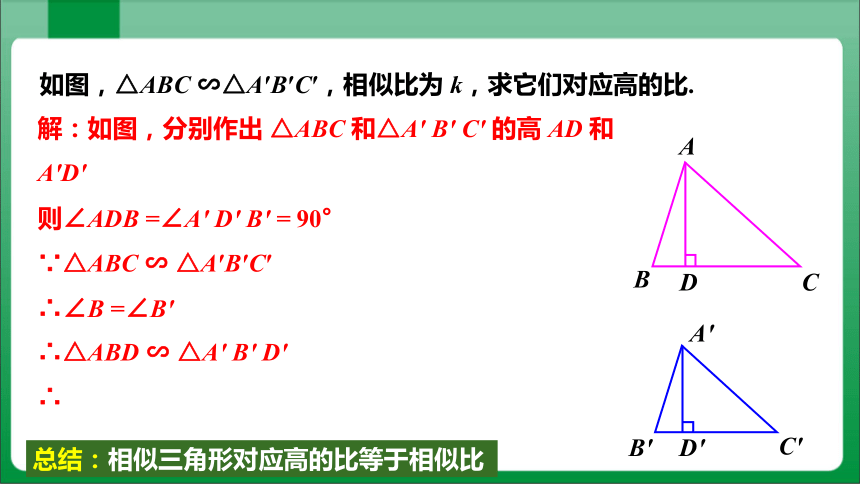
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应高的比.
∴△ABD ∽ △A' B' D'
∴
解:如图,分别作出 △ABC 和△A' B' C' 的高 AD 和 A'D'
则∠ADB =∠A' D' B' = 90°
∵△ABC ∽ △A′B′C′
∴∠B =∠B'
总结:相似三角形对应高的比等于相似比
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应角平分线的比.
A
B
C
A'
B'
C'
D'
D
解:如图,分别作出 △ABC 和△A' B' C' 的角平分线
AD 和 A'D',则∠BAD =∠B' A' D'
∵△ABC ∽△A′B′C′
∴∠B=∠B' ,
∴△ABD ∽△A' B' D'
∴
总结:相似三角形对应角平分线的比等于相似比
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应中线的比.
A
B
C
A'
B'
C'
D'
D
解:如图,分别作出 △ABC 和△A' B' C' 的中线AD 和 A'D',
则
∵△ABC ∽△A′B′C′
∴∠B=∠B' ,
∴△ABD ∽△A' B' D'
∴
总结:相似三角形对应中线的比等于相似比
解:如果 △ABC ∽△A'B'C',相似比为 k,那么
因此
AB = kA'B',BC = kB'C',CA = kC'A',
从而
思考
相似三角形的周长比也等于相似比吗?为什么?
总结:相似三角形对应中线的比等于相似比
综合以上四个结论有:相似三角形对应线段的比等于相似比
针对训练
1. 如果两个相似三角形的对应高的比为 2 : 3,那么对应角平分线的比是 ,对应边上的中线的比是______ .
2. 已知 △ABC ∽ △A'B'C' ,相似比为 3 : 4,若 BC 边上的高 AD = 12 cm,则 B'C' 边上的高 A'D' = ______ .
2 : 3
2 : 3
16 cm
3. 如图,△ABC 与 △A′B′C′ 相似,AD,BE 是 △ABC 的高,A′D′,B′E′ 是 △A′B′C′ 的高,求证
证明:∵△ABC ∽ △A′B′C′,AD,A′D′ 分别是 △ABC,△A′B′C′ 的高,
A
A′
B
C
D
E
B′
C′
D′
E′
又 BE,B′E′ 分别是 △ABC,△A′B′C′ 的高,
∴ ∴
∴
4.如图,在△ABC 中,两条中线 BE,CD 相交于点 O,则△EOD 的周长:△BOC的周长为( )
A.1:2 B.2:3 C.1:3 D.1:4
A
BE,CD是两条中线
DE 是△ABC 的中位线
DE//BC,SDDDD
△EOD∽△BOC
△EOD 的周长:
△BOC 的周长=1:2
5.如图,在△ABC 中,DE//BC,AH⊥BC 于点 H,与 DE 交于点 G.若 ,则 = , = .
DE//BC
△ADE ∽△ABC
∴△ADG∽△ABH
注意找准对应线段
二 相似三角形面积的比
思考
相似三角形的面积比也等于相似比吗?为什么?
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
由前面的结论,我们有
A
B
C
A'
B'
C'
D'
D
相似三角形面积的比等于相似比的平方.
总结:相似三角形面积的比等于
相似比的平方.
解:在 △ABC 和 △DEF 中,∵ AB = 2DE,AC = 2DF,
又 ∵∠D=∠A,
A
B
C
D
E
F
∴
例1 如图,在 △ABC 和 △DEF 中,AB = 2DE ,AC = 2DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
∴ △DEF ∽ △ABC ,相似比为
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
针对训练
1.判断题(正确的画“√”,错误的画“×”).
(1) 一个三角形的各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍. ( )
√
×
2.如图,在△ABC中,点D,E分别是AB,AC的中点,若△ADE的面积是3 cm2,则四边形BDEC的面积为( )
A.12cm2 B.9cm2 C.6cm2 D.3cm2
B
已知
DE 是△ABC 的中位线
DE//BC,
△ADE∽△ABC
S△ADE:S△ABC=1:4
相似比是1:2
S△ADE:S四边形BDEC=1:3
3.如图,在 ABCD中,E是CD的延长线上一点,BE与AD交于点F,且AF=2FD.
(1)求证:△ABF∽△CEB;
(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠CAB,
∴∠ABF=∠E,
在△ABF和△CEB中,∠A=∠C,∠ABF=∠E,
∴△ABF∽△CEB.
(2)若△CEB的面积为9,求 ABCD的面积.
(2)解:∵AF=2FD,∴AD=3FD,
∴DF∶BC=1∶3,
∵△CEB的面积为9,∴△FDE的面积为1,∴△ABF的面积为4,
∴ ABCD的面积=9-1+4=12.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC,
∴△ABF∽△DEF,△CEB∽△DEF,
∴S△ABF∶S△DEF=AF2∶FD2,S△BCE∶S△FDE=BC2∶FD2,
解:①当 AE:ED = 2:3时,AE:AD = 2:5.
∵ 四边形 ABCD 是平行四边形
1.(凉山州中考)在平行四边形 ABCD 中,E 是AD 上一点,且点 E 将 AD 分为2:3的两部分,连接 BE,AC 相交于 F,则 S△AEF:S△CBF = .
∴ AD//BC,AD = BC,
AE:BC =2:5.
∵△AEF∽△CBF,
∴ S△AEF:S△CBF = 4:25.
②当 AE:ED = 3:2时,AE:AD = 3:5,
同理可得, S△AEF:S△CBF = 9:25.
注意:
AE: ED要分两种情况讨论.
4:25 或 9:25
随堂练习
2.如图,在△ABC中,DE//BC,BF平分∠ABC,交DE的延长线于点F.若AD=1,BD=2,BC=4,则EF=______.
解析:∵DE//BC ∴∠F=∠FBC
∵BF平分∠ ABC
∴∠DBF=∠ FBC,∠ F=∠DBF,DB=DF
∵DE//BC ∴△ ADE∽△ ABC
∴ ,即 ,
∵DF=DB=2
∴
3.如图,D、E分别是△ ABC的边AB、BC上的点,DE//AC,若
,则 的值为( ).
A. B. C. D.
解析:∵
∴BE : EC = 1 : 3,BE : BC = 1 : 4
∵DE//AC
∴△ DOE∽△ COA,△ BDE∽△ BAC
∴
∴
D
4.如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为 ,若S=2,则 ( ).
A. 4 B. 6 C. 8 D.不能确定
C
解:过P作PQ//DC交BC于点Q,由DC//AB,得到PQ//AB,
∴四边形PQCD与四边形APQB都为平行四边形
∴△PDC ≌△CQP,△ABP ≌△QPB
∴
∵EF为△PCB的中位线
∴△PEF∽△ PBC,且相似比为1:2
∴
∴
相似三角形的性质
对应角相等
对应边成比例
对应高的比,对应中线的比、对应角平分线的比都等于相似比.
对应边的比叫做相似比
周长的比等于相似比
面积的比等于相似比的平方
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
27.2.4 相似三角形的性质
第二十七章 相似
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 理解并掌握相似三角形中对应线段的比等于相似比,并运用其解决问题.
2. 理解相似三角形面积的比等于相似比的平方,并运用其解决问题.
学习目标
重点
难点
1. 相似三角形的判定方法有哪几种?
①定义:对应边成比例,对应角相等的两个三角形相似;
②平行于三角形一边的直线与另外两边相交所构成的三角形与原三角形相似;
③三边成比例的两个三角形相似;
④两边成比例且夹角相等的两个三角形相似;
⑤两角分别相等的两个三角形相似;
⑥一组直角边和斜边成比例的两个直角三角形相似.
新课引入
2. 三角形中有各种各样的几何量,例如三条边的长度,三个内角的度数,高、中线、角平分线的长度,以及周长、面积等.如果两个三角形相似,那么它们的这些几何量之间有什么关系呢?
让我们一起来探究吧!
探究
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
新知学习
A
B
C
A'
B'
C'
D'
D
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应高的比.
∴△ABD ∽ △A' B' D'
∴
解:如图,分别作出 △ABC 和△A' B' C' 的高 AD 和 A'D'
则∠ADB =∠A' D' B' = 90°
∵△ABC ∽ △A′B′C′
∴∠B =∠B'
总结:相似三角形对应高的比等于相似比
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应角平分线的比.
A
B
C
A'
B'
C'
D'
D
解:如图,分别作出 △ABC 和△A' B' C' 的角平分线
AD 和 A'D',则∠BAD =∠B' A' D'
∵△ABC ∽△A′B′C′
∴∠B=∠B' ,
∴△ABD ∽△A' B' D'
∴
总结:相似三角形对应角平分线的比等于相似比
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应中线的比.
A
B
C
A'
B'
C'
D'
D
解:如图,分别作出 △ABC 和△A' B' C' 的中线AD 和 A'D',
则
∵△ABC ∽△A′B′C′
∴∠B=∠B' ,
∴△ABD ∽△A' B' D'
∴
总结:相似三角形对应中线的比等于相似比
解:如果 △ABC ∽△A'B'C',相似比为 k,那么
因此
AB = kA'B',BC = kB'C',CA = kC'A',
从而
思考
相似三角形的周长比也等于相似比吗?为什么?
总结:相似三角形对应中线的比等于相似比
综合以上四个结论有:相似三角形对应线段的比等于相似比
针对训练
1. 如果两个相似三角形的对应高的比为 2 : 3,那么对应角平分线的比是 ,对应边上的中线的比是______ .
2. 已知 △ABC ∽ △A'B'C' ,相似比为 3 : 4,若 BC 边上的高 AD = 12 cm,则 B'C' 边上的高 A'D' = ______ .
2 : 3
2 : 3
16 cm
3. 如图,△ABC 与 △A′B′C′ 相似,AD,BE 是 △ABC 的高,A′D′,B′E′ 是 △A′B′C′ 的高,求证
证明:∵△ABC ∽ △A′B′C′,AD,A′D′ 分别是 △ABC,△A′B′C′ 的高,
A
A′
B
C
D
E
B′
C′
D′
E′
又 BE,B′E′ 分别是 △ABC,△A′B′C′ 的高,
∴ ∴
∴
4.如图,在△ABC 中,两条中线 BE,CD 相交于点 O,则△EOD 的周长:△BOC的周长为( )
A.1:2 B.2:3 C.1:3 D.1:4
A
BE,CD是两条中线
DE 是△ABC 的中位线
DE//BC,SDDDD
△EOD∽△BOC
△EOD 的周长:
△BOC 的周长=1:2
5.如图,在△ABC 中,DE//BC,AH⊥BC 于点 H,与 DE 交于点 G.若 ,则 = , = .
DE//BC
△ADE ∽△ABC
∴△ADG∽△ABH
注意找准对应线段
二 相似三角形面积的比
思考
相似三角形的面积比也等于相似比吗?为什么?
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
由前面的结论,我们有
A
B
C
A'
B'
C'
D'
D
相似三角形面积的比等于相似比的平方.
总结:相似三角形面积的比等于
相似比的平方.
解:在 △ABC 和 △DEF 中,∵ AB = 2DE,AC = 2DF,
又 ∵∠D=∠A,
A
B
C
D
E
F
∴
例1 如图,在 △ABC 和 △DEF 中,AB = 2DE ,AC = 2DF,∠A = ∠D. 若 △ABC 的边 BC 上的高为 6,面积为 ,求 △DEF 的边 EF 上的高和面积.
∴ △DEF ∽ △ABC ,相似比为
∵△ABC 的边 BC 上的高为 6,面积为 ,
∴△DEF 的边 EF 上的高为 ×6 = 3,
面积为
针对训练
1.判断题(正确的画“√”,错误的画“×”).
(1) 一个三角形的各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍. ( )
√
×
2.如图,在△ABC中,点D,E分别是AB,AC的中点,若△ADE的面积是3 cm2,则四边形BDEC的面积为( )
A.12cm2 B.9cm2 C.6cm2 D.3cm2
B
已知
DE 是△ABC 的中位线
DE//BC,
△ADE∽△ABC
S△ADE:S△ABC=1:4
相似比是1:2
S△ADE:S四边形BDEC=1:3
3.如图,在 ABCD中,E是CD的延长线上一点,BE与AD交于点F,且AF=2FD.
(1)求证:△ABF∽△CEB;
(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠CAB,
∴∠ABF=∠E,
在△ABF和△CEB中,∠A=∠C,∠ABF=∠E,
∴△ABF∽△CEB.
(2)若△CEB的面积为9,求 ABCD的面积.
(2)解:∵AF=2FD,∴AD=3FD,
∴DF∶BC=1∶3,
∵△CEB的面积为9,∴△FDE的面积为1,∴△ABF的面积为4,
∴ ABCD的面积=9-1+4=12.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC,
∴△ABF∽△DEF,△CEB∽△DEF,
∴S△ABF∶S△DEF=AF2∶FD2,S△BCE∶S△FDE=BC2∶FD2,
解:①当 AE:ED = 2:3时,AE:AD = 2:5.
∵ 四边形 ABCD 是平行四边形
1.(凉山州中考)在平行四边形 ABCD 中,E 是AD 上一点,且点 E 将 AD 分为2:3的两部分,连接 BE,AC 相交于 F,则 S△AEF:S△CBF = .
∴ AD//BC,AD = BC,
AE:BC =2:5.
∵△AEF∽△CBF,
∴ S△AEF:S△CBF = 4:25.
②当 AE:ED = 3:2时,AE:AD = 3:5,
同理可得, S△AEF:S△CBF = 9:25.
注意:
AE: ED要分两种情况讨论.
4:25 或 9:25
随堂练习
2.如图,在△ABC中,DE//BC,BF平分∠ABC,交DE的延长线于点F.若AD=1,BD=2,BC=4,则EF=______.
解析:∵DE//BC ∴∠F=∠FBC
∵BF平分∠ ABC
∴∠DBF=∠ FBC,∠ F=∠DBF,DB=DF
∵DE//BC ∴△ ADE∽△ ABC
∴ ,即 ,
∵DF=DB=2
∴
3.如图,D、E分别是△ ABC的边AB、BC上的点,DE//AC,若
,则 的值为( ).
A. B. C. D.
解析:∵
∴BE : EC = 1 : 3,BE : BC = 1 : 4
∵DE//AC
∴△ DOE∽△ COA,△ BDE∽△ BAC
∴
∴
D
4.如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为 ,若S=2,则 ( ).
A. 4 B. 6 C. 8 D.不能确定
C
解:过P作PQ//DC交BC于点Q,由DC//AB,得到PQ//AB,
∴四边形PQCD与四边形APQB都为平行四边形
∴△PDC ≌△CQP,△ABP ≌△QPB
∴
∵EF为△PCB的中位线
∴△PEF∽△ PBC,且相似比为1:2
∴
∴
相似三角形的性质
对应角相等
对应边成比例
对应高的比,对应中线的比、对应角平分线的比都等于相似比.
对应边的比叫做相似比
周长的比等于相似比
面积的比等于相似比的平方
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
