5.8正多边形和圆 第1课时 圆内接正多边形 同步练习(含答案)
文档属性
| 名称 | 5.8正多边形和圆 第1课时 圆内接正多边形 同步练习(含答案) | 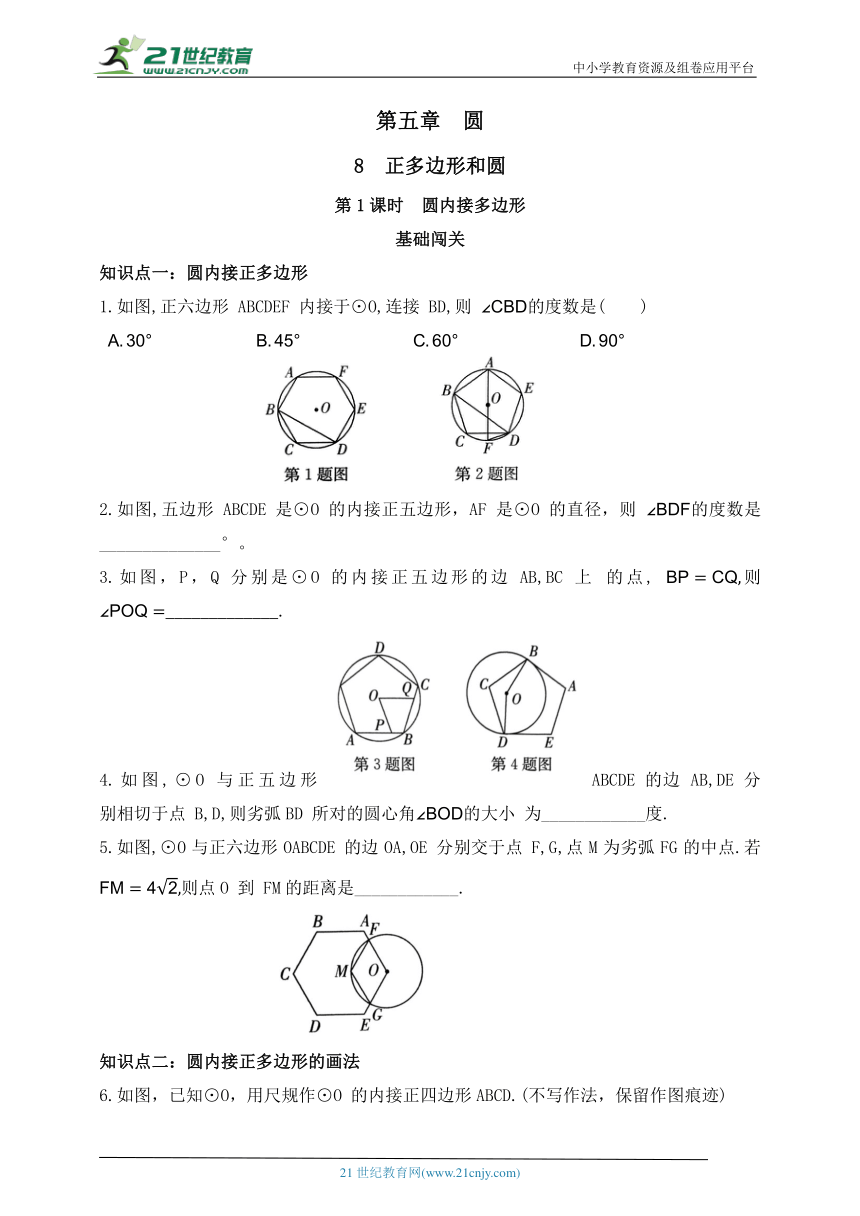 | |
| 格式 | docx | ||
| 文件大小 | 40.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 16:55:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 圆
8 正多边形和圆
第1课时 圆内接多边形
基础闯关
知识点一:圆内接正多边形
1.如图,正六边形 ABCDEF 内接于⊙O,连接 BD,则 的度数是( )
2.如图,五边形ABCDE 是⊙O 的内接正五边形,AF 是⊙O 的直径,则 的度数是______________°。
3.如图,P,Q 分别是⊙O 的内接正五边形的边AB,BC 上 的点, 则 _____________.
4.如图,⊙O 与正五边形ABCDE的边 AB,DE 分别相切于点 B,D,则劣弧BD 所对的圆心角的大小 为____________度.
5.如图,⊙O与正六边形OABCDE 的边OA,OE 分别交于点 F,G,点M为劣弧FG的中点.若则点O 到 FM的距离是____________.
知识点二:圆内接正多边形的画法
6.如图,已知⊙O,用尺规作⊙O 的内接正四边形ABCD.(不写作法,保留作图痕迹)
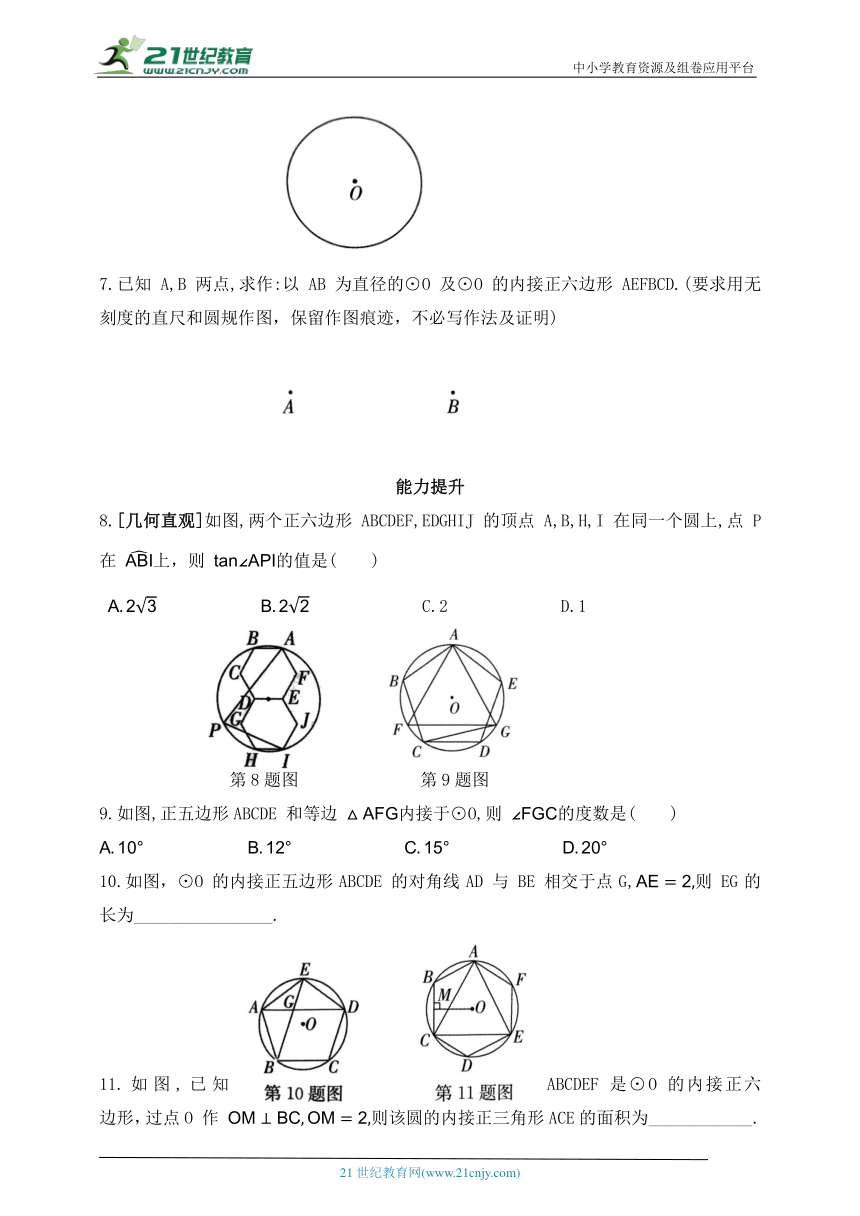
7.已知 A,B 两点,求作:以AB 为直径的⊙O及⊙O 的内接正六边形 AEFBCD.(要求用无刻度的直尺和圆规作图,保留作图痕迹,不必写作法及证明)
能力提升
8.[几何直观]如图,两个正六边形 ABCDEF,EDGHIJ 的顶点A,B,H,I在同一个圆上,点 P 在 上,则 的值是( )
C.2 D.1
第8题图 第9题图
9.如图,正五边形ABCDE 和等边 内接于⊙O,则 的度数是( )
10.如图,⊙O 的内接正五边形ABCDE 的对角线AD 与 BE 相交于点G,则 EG的长为________________.
11.如图,已知 ABCDEF 是⊙O 的内接正六边形,过点O 作 则该圆的内接正三角形ACE的面积为____________.
12.如图,已知⊙O的内接正方形ABCD,E 为边CD 上一点,且 延长BE 交⊙O于点F,连接FC,若正方形的边长为1,则弦FC的长为______________.
13.[空间观念]已知四个正六边形按如图所示的方式摆放在圆中,顶点 A,B,C,D,E,F在圆上.若两个大正六边形的边长均为 4,则小正六边形的边长是_____________.
14.[推理能力]如图,五边形 DEFGH 是边长为1的正五边形,⊙O 是正五边形DEFGH 的外接圆,过点 D 作⊙O 的切线,与GH,FE的延长线分别交于点 B 和C,延长 HG,EF相交于点A,连接GD,DF,下列结论正确的是____________.(填序号)
为等腰三角形;
③四边形 AGDF 为菱形;
的周长为
培优创新
15.如图,在⊙O 的内接四边形ABCD中, 点 E 在弧AD 上,连接AE,DE.
(1)求 的度数.
(2)当 时,AE 恰好为⊙O 的内接正n边形的一边,求n的值.
参考答案
1. A 2.54 4.144
[解析]如图,连接OM,过点O 作于点H.∵OABCDE 为正六边形, 点M 为劣弧FG 的中点,.
6.解:如图所示,四边形ABCD即为所求.
7.解:如图所示,⊙O及六边形AEFBCD 即为所求.
8. A [解析]如图,连接AE,EI,AH,过点 J 作JM⊥EI 于点M.∵ABCDEF 是正六边形,∴∠DEF=∠F=120°.∵FA=FE,∴∠FEA=∠FAE=30°,∴∠AED=90°.同理,∠DEI=∠EIH=90°,∴∠AED+∠DEI =180°,∴点A,E,I 共线.设 IH=IJ =JE=a.∵JM⊥EI,
9. B
[解析]设E G=x,易知:∠AEB=∠ABE=∠EAG=36°,∠BAG=∠AGB=72°,∴AB=BG=AE=2.∵∠AEG=∠AEB,∠EAG=∠EBA,∴△AEG∽,解得 x=或 (舍去),∴EG= -1.
11.4 [解析]如图所示,连接OC,OB,过点 O作( CE 于点N.∵多边形ABCDEF 是正六边形,∴∠COB=60°.∵OC=OB,∴△COB 是等边三角形,∴∠OCM=该圆的内接正三角形ACE的面积
[解析]如图,连接 BD. 在 Rt△ABD中,BD== .∵∠DBE=∠FCE,∠CFE=∠BDE,
[解析]如图,连接AD交 PM于点O,则点O是圆心,过点O作ON⊥DE 于点N,连接MF,取MF的中点G,连接GH,GQ.由对称性可知:OM=OP=EN=DN=2,由正六边形的性质可得 由正六边形的性质可知:△GFH,△GHQ,△GQM 都是正三角形,
14.①②③ [解析]根据多边形的内角求解公式可知:
故①正确.∵五边形DEFGH 是边长为1的正五边形, 由题易知GF∥BC,∴∠B=∠C,∴△ABC 为等腰三角形,故②正确.由题易知∠DFE=∠GDF=∠DGB,BD
∴AF=DG,AG=DF.∵AB=AC,∴四边形AGDF 为菱形,故③正确.设 DF=AF=FC=x,∵∠GFE=∠DEF,∴∠AFG=∠DEC=∠AGF=∠B,∴△ABC∽△即 (舍去),的周长为 故④错误.
15.解:(1)如图,连接BD.∵四边形ABCD 是⊙O 的内接四边形,∴∠BAD+∠C=180°.∵∠C=120°,∴∠BAD=60°.∵AB = AD,∴△ABD 是等边三角形,∴∠ABD=60°.∵四边形 ABDE 是⊙O的内接四边形,∴∠AED+∠ABD=180°,∴∠AED=120°.
(2)连接 OA,OE,OD.∵∠ABD=60°,∴∠AOD=2∠ABD=120°.∵∠DOE=90°,∴∠AOE=∠AOD-
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 圆
8 正多边形和圆
第1课时 圆内接多边形
基础闯关
知识点一:圆内接正多边形
1.如图,正六边形 ABCDEF 内接于⊙O,连接 BD,则 的度数是( )
2.如图,五边形ABCDE 是⊙O 的内接正五边形,AF 是⊙O 的直径,则 的度数是______________°。
3.如图,P,Q 分别是⊙O 的内接正五边形的边AB,BC 上 的点, 则 _____________.
4.如图,⊙O 与正五边形ABCDE的边 AB,DE 分别相切于点 B,D,则劣弧BD 所对的圆心角的大小 为____________度.
5.如图,⊙O与正六边形OABCDE 的边OA,OE 分别交于点 F,G,点M为劣弧FG的中点.若则点O 到 FM的距离是____________.
知识点二:圆内接正多边形的画法
6.如图,已知⊙O,用尺规作⊙O 的内接正四边形ABCD.(不写作法,保留作图痕迹)
7.已知 A,B 两点,求作:以AB 为直径的⊙O及⊙O 的内接正六边形 AEFBCD.(要求用无刻度的直尺和圆规作图,保留作图痕迹,不必写作法及证明)
能力提升
8.[几何直观]如图,两个正六边形 ABCDEF,EDGHIJ 的顶点A,B,H,I在同一个圆上,点 P 在 上,则 的值是( )
C.2 D.1
第8题图 第9题图
9.如图,正五边形ABCDE 和等边 内接于⊙O,则 的度数是( )
10.如图,⊙O 的内接正五边形ABCDE 的对角线AD 与 BE 相交于点G,则 EG的长为________________.
11.如图,已知 ABCDEF 是⊙O 的内接正六边形,过点O 作 则该圆的内接正三角形ACE的面积为____________.
12.如图,已知⊙O的内接正方形ABCD,E 为边CD 上一点,且 延长BE 交⊙O于点F,连接FC,若正方形的边长为1,则弦FC的长为______________.
13.[空间观念]已知四个正六边形按如图所示的方式摆放在圆中,顶点 A,B,C,D,E,F在圆上.若两个大正六边形的边长均为 4,则小正六边形的边长是_____________.
14.[推理能力]如图,五边形 DEFGH 是边长为1的正五边形,⊙O 是正五边形DEFGH 的外接圆,过点 D 作⊙O 的切线,与GH,FE的延长线分别交于点 B 和C,延长 HG,EF相交于点A,连接GD,DF,下列结论正确的是____________.(填序号)
为等腰三角形;
③四边形 AGDF 为菱形;
的周长为
培优创新
15.如图,在⊙O 的内接四边形ABCD中, 点 E 在弧AD 上,连接AE,DE.
(1)求 的度数.
(2)当 时,AE 恰好为⊙O 的内接正n边形的一边,求n的值.
参考答案
1. A 2.54 4.144
[解析]如图,连接OM,过点O 作于点H.∵OABCDE 为正六边形, 点M 为劣弧FG 的中点,.
6.解:如图所示,四边形ABCD即为所求.
7.解:如图所示,⊙O及六边形AEFBCD 即为所求.
8. A [解析]如图,连接AE,EI,AH,过点 J 作JM⊥EI 于点M.∵ABCDEF 是正六边形,∴∠DEF=∠F=120°.∵FA=FE,∴∠FEA=∠FAE=30°,∴∠AED=90°.同理,∠DEI=∠EIH=90°,∴∠AED+∠DEI =180°,∴点A,E,I 共线.设 IH=IJ =JE=a.∵JM⊥EI,
9. B
[解析]设E G=x,易知:∠AEB=∠ABE=∠EAG=36°,∠BAG=∠AGB=72°,∴AB=BG=AE=2.∵∠AEG=∠AEB,∠EAG=∠EBA,∴△AEG∽,解得 x=或 (舍去),∴EG= -1.
11.4 [解析]如图所示,连接OC,OB,过点 O作( CE 于点N.∵多边形ABCDEF 是正六边形,∴∠COB=60°.∵OC=OB,∴△COB 是等边三角形,∴∠OCM=该圆的内接正三角形ACE的面积
[解析]如图,连接 BD. 在 Rt△ABD中,BD== .∵∠DBE=∠FCE,∠CFE=∠BDE,
[解析]如图,连接AD交 PM于点O,则点O是圆心,过点O作ON⊥DE 于点N,连接MF,取MF的中点G,连接GH,GQ.由对称性可知:OM=OP=EN=DN=2,由正六边形的性质可得 由正六边形的性质可知:△GFH,△GHQ,△GQM 都是正三角形,
14.①②③ [解析]根据多边形的内角求解公式可知:
故①正确.∵五边形DEFGH 是边长为1的正五边形, 由题易知GF∥BC,∴∠B=∠C,∴△ABC 为等腰三角形,故②正确.由题易知∠DFE=∠GDF=∠DGB,BD
∴AF=DG,AG=DF.∵AB=AC,∴四边形AGDF 为菱形,故③正确.设 DF=AF=FC=x,∵∠GFE=∠DEF,∴∠AFG=∠DEC=∠AGF=∠B,∴△ABC∽△即 (舍去),的周长为 故④错误.
15.解:(1)如图,连接BD.∵四边形ABCD 是⊙O 的内接四边形,∴∠BAD+∠C=180°.∵∠C=120°,∴∠BAD=60°.∵AB = AD,∴△ABD 是等边三角形,∴∠ABD=60°.∵四边形 ABDE 是⊙O的内接四边形,∴∠AED+∠ABD=180°,∴∠AED=120°.
(2)连接 OA,OE,OD.∵∠ABD=60°,∴∠AOD=2∠ABD=120°.∵∠DOE=90°,∴∠AOE=∠AOD-
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
