4.3 角(第2课时) 课件(共29张PPT)-【大单元教学】2023-2024学年七年级数学上册同步备课系列(人教版)
文档属性
| 名称 | 4.3 角(第2课时) 课件(共29张PPT)-【大单元教学】2023-2024学年七年级数学上册同步备课系列(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 619.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览







文档简介
新课导入
讲授新课
当堂检测
课堂小结
第四章 几何图形初步
4.3 角
4.3.2 角的比较与运算
情景引入
情景引入
如果你要爬上这座山顶,你选择从哪一面上山呢?
知识点一 角的比较与计算
知识精讲
如何比较两条线段的长短?
从“数”的角度进行比较(度量法).
用有刻度的直尺分别量出两条线段的长度,进行数量的比较.
知识精讲
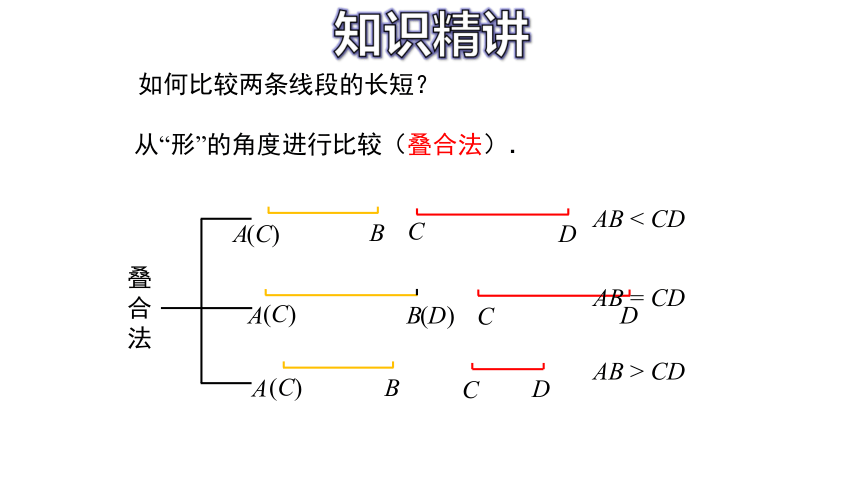
叠合法
如何比较两条线段的长短?
C
D
B
(C)
从“形”的角度进行比较(叠合法).
A
AB < CD
C
D
B
A
(C)
AB > CD
C
D
B
A
(C)
(D)
AB = CD
知识精讲
类比线段长短的比较方法,如何比较两个角的大小?
1.观察法
如图,通过观察,我们可以知道∠1比∠2小。
记作∠1<∠2或∠2>∠1.
?
1
2
知识精讲
类比线段长短的比较方法,如何比较两个角的大小?
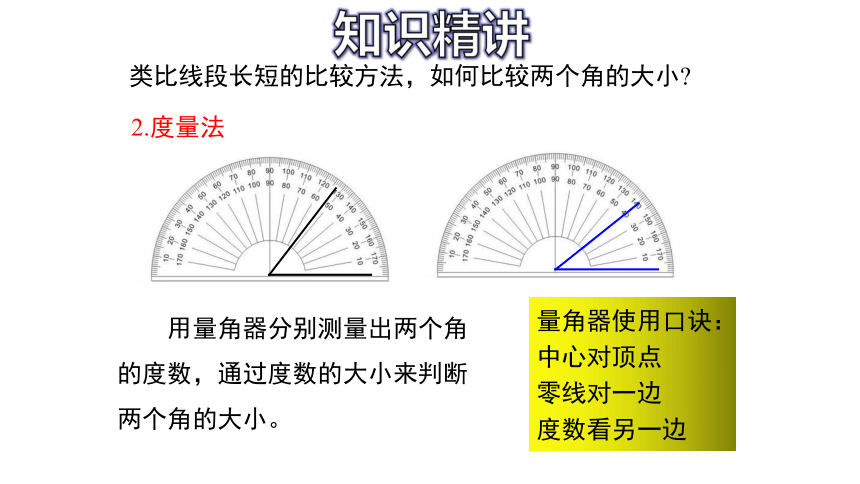
2.度量法
用量角器分别测量出两个角的度数,通过度数的大小来判断两个角的大小。
量角器使用口诀:
中心对顶点
零线对一边
度数看另一边
知识精讲
类比线段长短的比较方法,如何比较两个角的大小?
3. 叠合法
A
B
O
(O')
B'
( A' )
A
B
O
A
B
O
你能用图形和几何语言说明两个角的大小关系吗?
(两个角分别记作∠AOB,∠A'O'B')
(O')
B'
(A')
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O')
(B')
(A')
知识精讲
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小。
重点:
1、两角的顶点必须重合;
2、一边必须重合,另一边落在重合的一边的同侧。
知识精讲
比较角的方法
(1)直接观察法;
(2)度量法:用量角器量出它们的度数,再进行比较;
(2)叠合法:将两个角的顶点及一条边重合,另一条边放在重合边的同侧就可以比较大小.
典型例题
典例精析
【例1】把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除
练一练
1、已知∠α,用量角器求作一个角,使它等于∠α.
作法:
1、用量角器量得∠α =40°.
2、作射线OA .
3、用量角器作射线OB,使∠AOB=40°.
∠AOB=40°= ∠α ,∠AOB就是所求作的角.
知识点二 角平分线
知识精讲
B
A
O
C
探究
在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
知识精讲
从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
如图:OC是∠AOB的平分线.
A
B
C
O
1
2
注意:角平分线是一条射线.
知识精讲
A
B
C
O
1
2
如图,OC是∠AOB的角平分线.
∵OC是∠AOB的角平分线
∴∠AOC=∠COB=12∠AOB
或∠AOB=2∠AOC=2∠COB
?
反过来:
∵∠AOC=∠COB=12∠AOB
或∠AOB=2∠AOC=2∠COB
?
∴OC是∠AOB的角平分线
知识精讲
角的????等分线
?
角的角平分线将角两等分,我们还可以将角三等分、四等分.....
如图射线OC、OD将∠AOB分成相等的三个角,射线OC、OD叫∠AOB的三等分线.
∠AOC=∠COD=∠DOB=13∠AOB或∠AOB=3∠AOC=3∠COD=3∠DOB
?
角的角平分线有1条,角的三等分线有2条,角四等分线有
3条,...,角的????等分线有(????-1)条,将角分成相等的????个角.
?
典型例题
典例精析
【例2】如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解:因为 OB 平分∠AOC,
∠AOC=80°,
O
A
B
C
D
E
所以
∠BOC= ∠AOC
= ×80°=40°.
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
解:因为 OB 平分∠AOC,
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE,
所以∠COD=∠DOE = 30°,
所以
∠BOD =∠BOC+∠COD = 40°+30°= 70°.
O
A
B
C
D
E
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB
是多少度?
解:因为 ∠COD=30°,
OD 平分∠COE,
所以 ∠COE=2∠COD=60°,
所以 ∠AOC=∠AOE-∠COE
=140°-60°= 80°.
又因为 OB 平分∠AOC,
O
A
B
C
D
E
所以
∠AOB= ∠AOC= ×80°= 40°.
练一练
1、如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=35°,则∠AOD等于多少度?
A
B
O
D
C
解:由题意可知
∵OC是∠DOB的角平分线,且COB=35°
∴∠BOD=2∠COB=2×35°=70°
又∵∠AOB是平角
∴∠AOD+∠BOD=∠AOB
∠AOD=∠AOB-∠BOD
=180°-70° =110°
2、如图,已知OC是∠AOB的平分线,OD是∠BOC的平分线,若∠COD=25°,求∠AOB的度数.
解:OC是∠AOB的平分线,
∴∠AOB=2∠BOC
∵OD是∠BOC的平分线,
∴∠BOC=2∠COD
∵∠COD=25°,
∴∠BOC=2∠COD=50°
∴∠AOB=2∠BOC=100°
?
课堂练习
2.如图,∠AOB=50°,OC平分∠AOB,则∠AOC=________°.
1.比较大小:74.45°________74°45′(填“>”“<”或“=”).
<
25
3.将两块相同的直角三角板的顶点重合(如图所示),则∠1与∠2的大小关系是( )
A.∠1>∠2
B.∠1<∠2
C.∠1=∠2
D.以上结论都有可能
C
4.如图,OC,OD分别是∠AOB,∠BOC的平分线,且∠COD=25°,则∠AOB的度数是( )
A.100° B.120°
C.135° D.150°
A
5、如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( )
A.70°
B.30°
C.25°
D.20°
A
6.如图,∠AOD=120°,∠2=2∠1=60°,求:
(1)∠DOC的度数;
(2)∠BOD的度数.
解:(1)∠DOC=∠AOD-∠2=120°-60°=60°
(2)∠BOD=∠AOD+∠AOB=120°+30°=150°
(1).120°-38°41′;
(2).67°31′+48°49′.
解:原式 = 119°60′-38°41′
= 81°19′.
解:原式 = (67+48)°+(31+49)′
= 115°97′
= 116°37′.
7.计算:
8.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.
O
A
D
C
B
解:设∠COD=x,
∵∠AOC=60°,∠BOD=90°,
∴∠AOD=60°-x,
∴∠AOB=90°+60°-x=150°-x,
∵∠AOB是∠DOC的3倍,
∴150°-x=3x,解得x=37.5°,
∴∠AOB=3×37.5°=112.5°.
解:
设∠BOC=2x°,
则∠AOE=5x°,∠AOD=8x°.
因为O是直线AB上一点,
所以∠AOB=180°,
所以∠COE=(180-7x)°.
因为OE平分∠AOC,
所以∠AOE=∠COE,
即5x=180-7x,
解得x=15,
所以∠AOD=8×15°=120°,
所以∠BOD=60°.
9.如图,O是直线AB上一点,OC,OD是从O点引出的两条射线,OE平分∠AOC,∠BOC?∠AOE : ∠AOD=2 : 5 : 8,求∠BOD的度数.
课堂总结
角的比较
角的平分线
度量法
叠合法
角的运算
加与减
乘与除
角的和差倍分关系
角的计算
讲授新课
当堂检测
课堂小结
第四章 几何图形初步
4.3 角
4.3.2 角的比较与运算
情景引入
情景引入
如果你要爬上这座山顶,你选择从哪一面上山呢?
知识点一 角的比较与计算
知识精讲
如何比较两条线段的长短?
从“数”的角度进行比较(度量法).
用有刻度的直尺分别量出两条线段的长度,进行数量的比较.
知识精讲
叠合法
如何比较两条线段的长短?
C
D
B
(C)
从“形”的角度进行比较(叠合法).
A
AB < CD
C
D
B
A
(C)
AB > CD
C
D
B
A
(C)
(D)
AB = CD
知识精讲
类比线段长短的比较方法,如何比较两个角的大小?
1.观察法
如图,通过观察,我们可以知道∠1比∠2小。
记作∠1<∠2或∠2>∠1.
?
1
2
知识精讲
类比线段长短的比较方法,如何比较两个角的大小?
2.度量法
用量角器分别测量出两个角的度数,通过度数的大小来判断两个角的大小。
量角器使用口诀:
中心对顶点
零线对一边
度数看另一边
知识精讲
类比线段长短的比较方法,如何比较两个角的大小?
3. 叠合法
A
B
O
(O')
B'
( A' )
A
B
O
A
B
O
你能用图形和几何语言说明两个角的大小关系吗?
(两个角分别记作∠AOB,∠A'O'B')
(O')
B'
(A')
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O')
(B')
(A')
知识精讲
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小。
重点:
1、两角的顶点必须重合;
2、一边必须重合,另一边落在重合的一边的同侧。
知识精讲
比较角的方法
(1)直接观察法;
(2)度量法:用量角器量出它们的度数,再进行比较;
(2)叠合法:将两个角的顶点及一条边重合,另一条边放在重合边的同侧就可以比较大小.
典型例题
典例精析
【例1】把一个周角 7 等分,每一份是多少度的角 (精确到分)?
解:360°÷7 = 51°+3°÷7
= 51°+180′÷7
≈ 51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除
练一练
1、已知∠α,用量角器求作一个角,使它等于∠α.
作法:
1、用量角器量得∠α =40°.
2、作射线OA .
3、用量角器作射线OB,使∠AOB=40°.
∠AOB=40°= ∠α ,∠AOB就是所求作的角.
知识点二 角平分线
知识精讲
B
A
O
C
探究
在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
知识精讲
从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
如图:OC是∠AOB的平分线.
A
B
C
O
1
2
注意:角平分线是一条射线.
知识精讲
A
B
C
O
1
2
如图,OC是∠AOB的角平分线.
∵OC是∠AOB的角平分线
∴∠AOC=∠COB=12∠AOB
或∠AOB=2∠AOC=2∠COB
?
反过来:
∵∠AOC=∠COB=12∠AOB
或∠AOB=2∠AOC=2∠COB
?
∴OC是∠AOB的角平分线
知识精讲
角的????等分线
?
角的角平分线将角两等分,我们还可以将角三等分、四等分.....
如图射线OC、OD将∠AOB分成相等的三个角,射线OC、OD叫∠AOB的三等分线.
∠AOC=∠COD=∠DOB=13∠AOB或∠AOB=3∠AOC=3∠COD=3∠DOB
?
角的角平分线有1条,角的三等分线有2条,角四等分线有
3条,...,角的????等分线有(????-1)条,将角分成相等的????个角.
?
典型例题
典例精析
【例2】如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解:因为 OB 平分∠AOC,
∠AOC=80°,
O
A
B
C
D
E
所以
∠BOC= ∠AOC
= ×80°=40°.
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
解:因为 OB 平分∠AOC,
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE,
所以∠COD=∠DOE = 30°,
所以
∠BOD =∠BOC+∠COD = 40°+30°= 70°.
O
A
B
C
D
E
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB
是多少度?
解:因为 ∠COD=30°,
OD 平分∠COE,
所以 ∠COE=2∠COD=60°,
所以 ∠AOC=∠AOE-∠COE
=140°-60°= 80°.
又因为 OB 平分∠AOC,
O
A
B
C
D
E
所以
∠AOB= ∠AOC= ×80°= 40°.
练一练
1、如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=35°,则∠AOD等于多少度?
A
B
O
D
C
解:由题意可知
∵OC是∠DOB的角平分线,且COB=35°
∴∠BOD=2∠COB=2×35°=70°
又∵∠AOB是平角
∴∠AOD+∠BOD=∠AOB
∠AOD=∠AOB-∠BOD
=180°-70° =110°
2、如图,已知OC是∠AOB的平分线,OD是∠BOC的平分线,若∠COD=25°,求∠AOB的度数.
解:OC是∠AOB的平分线,
∴∠AOB=2∠BOC
∵OD是∠BOC的平分线,
∴∠BOC=2∠COD
∵∠COD=25°,
∴∠BOC=2∠COD=50°
∴∠AOB=2∠BOC=100°
?
课堂练习
2.如图,∠AOB=50°,OC平分∠AOB,则∠AOC=________°.
1.比较大小:74.45°________74°45′(填“>”“<”或“=”).
<
25
3.将两块相同的直角三角板的顶点重合(如图所示),则∠1与∠2的大小关系是( )
A.∠1>∠2
B.∠1<∠2
C.∠1=∠2
D.以上结论都有可能
C
4.如图,OC,OD分别是∠AOB,∠BOC的平分线,且∠COD=25°,则∠AOB的度数是( )
A.100° B.120°
C.135° D.150°
A
5、如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( )
A.70°
B.30°
C.25°
D.20°
A
6.如图,∠AOD=120°,∠2=2∠1=60°,求:
(1)∠DOC的度数;
(2)∠BOD的度数.
解:(1)∠DOC=∠AOD-∠2=120°-60°=60°
(2)∠BOD=∠AOD+∠AOB=120°+30°=150°
(1).120°-38°41′;
(2).67°31′+48°49′.
解:原式 = 119°60′-38°41′
= 81°19′.
解:原式 = (67+48)°+(31+49)′
= 115°97′
= 116°37′.
7.计算:
8.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.
O
A
D
C
B
解:设∠COD=x,
∵∠AOC=60°,∠BOD=90°,
∴∠AOD=60°-x,
∴∠AOB=90°+60°-x=150°-x,
∵∠AOB是∠DOC的3倍,
∴150°-x=3x,解得x=37.5°,
∴∠AOB=3×37.5°=112.5°.
解:
设∠BOC=2x°,
则∠AOE=5x°,∠AOD=8x°.
因为O是直线AB上一点,
所以∠AOB=180°,
所以∠COE=(180-7x)°.
因为OE平分∠AOC,
所以∠AOE=∠COE,
即5x=180-7x,
解得x=15,
所以∠AOD=8×15°=120°,
所以∠BOD=60°.
9.如图,O是直线AB上一点,OC,OD是从O点引出的两条射线,OE平分∠AOC,∠BOC?∠AOE : ∠AOD=2 : 5 : 8,求∠BOD的度数.
课堂总结
角的比较
角的平分线
度量法
叠合法
角的运算
加与减
乘与除
角的和差倍分关系
角的计算
