第5章 平面直角坐标系(小结与思考)单元复习 课件(共40张PPT)-2023-2024学年八年级数学上册同步精品课堂(苏科版)
文档属性
| 名称 | 第5章 平面直角坐标系(小结与思考)单元复习 课件(共40张PPT)-2023-2024学年八年级数学上册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 05:49:36 | ||
图片预览











文档简介
第5章 · 平面直角坐标系
小结与思考
学习目标
2. 掌握在平面直角坐标系中确定点的坐标描出点的位置的方法;
1. 理解物体的位置变化可以通过确定物体位置的数量变化来说明;
3. 掌握简单的对称图形、图形的平移的坐标关系.
知识框架
物体位置的确定
平面直角坐标系
条件
平面直角坐标系
概念和表示方法
1.区域定位法;2.经纬度定位法;3.方格定位法;
4.行列定位法;5.“方向角+距离”定位法
在平面内,确定一个物体的位置,一般需要两个数据
点的坐标
相关概念
平面直角坐标系;横轴与纵轴;原点;坐标;象限
各象限内点的坐标特征
第一象限:(+,+);第二象限:(-,+)第三象限:(-,-);第四象限:(+,-)
坐标轴上点坐标的特征
x轴上的点,表示为(x,0);
y轴上的点,表示为(0,y).
图形变换与点的坐标变化规律
轴对称
关于x轴对称的点的坐标特征:“纵”变,“横”不变
关于y轴对称的点的坐标特征:“横”变,“纵”不变
平移
左右平移,横坐标“左加右减”
上下平移,纵坐标“上加下减”
考点分析
考点一 位置的确定
例 如图是小军家与周围地区的行走路线示意图,相对小军家来说:
①小军家北偏东30°的方向上有 ; ②要想确定照相馆的位置,还需要 个数据; ③要确定小军家附近的学校的位置,需要 个数据,分别是 .
照相馆
超市
学校
小军家
30°
照相馆、超市
1
2
方向和距离
巩固练习
1.下列表述中,位置确定的是( )
A.北偏东30° B.东经118°,北纬24°
C.淮海路以北,中山路以南 D.银座电影院第2排
B
2.某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A.第3组第2排 B.第3组第1排 C.第2组第3排 D.第2组第2排
C
巩固练习
3. 如图,点O、M、A、B、C在同一平面内.若规定点A的位置记为(50,20°),点B的位置记为(30,60°),则点C的位置应记为________________.
(34,110°)
巩固练习
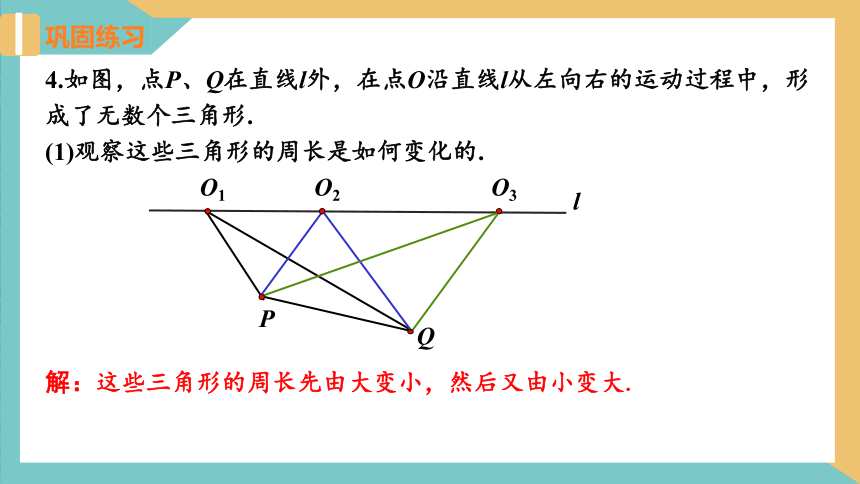
4.如图,点P、Q在直线l外,在点O沿直线l从左向右的运动过程中,形成了无数个三角形.
(1)观察这些三角形的周长是如何变化的.
O1
l
O2
O3
P
Q
解:这些三角形的周长先由大变小,然后又由小变大.
巩固练习
(2)这无数个三角形的周长有没有最小值?有没有最大值?如果有,试确定点O的位置.
P
Q
O
l
P′
O1
例 在平面直角坐标系中,
(1)已知点P(a﹣1,3a+6)在y轴上,求点P的坐标;
解:(1)∵点P(a﹣1,3a+6)在y轴上,
∴a﹣1=0,解得a=1,
∴3a+6=3×1+6=9,
∴P(0,9).
考点分析
考点二 平面直角坐标系中点的坐标特征
解:(2)∵AB∥x轴,
∴m=4,
∵点B在第一象限,
∴n>0,
∴m=4,n>0.
考点分析
(2)已知两点A(﹣3,m),B(n,4),若AB∥x轴,点B在第一象限,求m的值,并确定n的取值范围;
解:(3)∵AB=5,A、B的纵坐标都为4,
∴点P到AB的距离为9-4=5,
∴以P、A、B为顶点的三角形的面积:
S=????????×5×5=12.5.
?
考点分析
(3)在(1)(2)的条件下,如果线段AB的长度是5,求以P、A、B为顶点的三角形的面积S.
巩固练习
1.已知点M(1-2m,m-1)在第四象限,则m的取值范围是________.
解:由题意,得?????????????>????,①?????????<????,??②
由①得m<0.5,
由②得m<1,
∴m的取值范围是 m< 0.5.
?
m< 0.5
巩固练习
2.点P(2a﹣1,a+2)在x轴上,则点P的坐标为__________.
解:由题意,得
a+2=0,
解得a=﹣2,
2a﹣1=﹣5,
点P的坐标为(﹣5,0).
(﹣5,0)
巩固练习
3.若点A(6,6),AB∥x轴,且AB=2,则B点坐标为( )
A.(4,6) B.(6,4)或(6,8)
C.(6,4) D.(4,6)或(8,6)
解:∵A(6,6),AB∥x轴,
∴点B的纵坐标为6,
点B在点A的左边时,6﹣2=4,
此时点B的坐标为(4,6),
点B在点A的右边时,6+2=8,
此时,点B的坐标为(8,6),
综上所述,点B的坐标为(4,6)或(8,6).
D
巩固练习
4.如图,点A坐标为(3,0),B是y轴正半轴上一点,AB=5,则点B的坐标为( )
A.(4,0) B.(0,4) C.(0,5) D.(0,????????)
?
解:∵点A坐标为(3,0),B是y轴正半轴上一点,AB=5,
∴OB=?????????????????????????=?????????????????=4
∴点B的坐标为(0,4).
?
O
x
y
A
B
B
巩固练习
5. 已知平面直角坐标系中有一点M(m﹣1,2m+3)
(1)当m为何值时,点M到x轴的距离为1?
(2)当m为何值时,点M到y轴的距离为2?
解:(1)∵|2m+3|=1
2m+3=1或2m+3=﹣1
∴m=﹣1或m=﹣2;
(2)∵|m﹣1|=2
m﹣1=2或m﹣1=﹣2
∴m=3或m=﹣1.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(2)(1)中的△A'B'D的面积为____.?
考点分析
考点三 关于坐标轴对称的点的坐标特征
例 在平面直角坐标系xOy中,已知A(-1,4),B(4,2),C(-1,0)三点.
(1)点A关于y轴的对称点A′的坐标为 ,点B关于x轴的对称点B′的坐标为_______,线段AC的垂直平分线与y轴的交点D的坐标为_______;?
(1,4)
(4,-2)
(0,2)
O
x
y
解:(2)如图,△A'B'D的面积为
4×6-????????×4×4-????????×1×2-????????×3×6=6.
?
6
B
A
C
A′
B′
D
巩固练习
1.在平面直角坐标系中,点P(a,-6)关于x轴对称点为Q(2,b),则a+b的值为( )
A.﹣8 B.8 C. - 4 D.4
解:∵点P(a, -6)与点Q(2,b)关于x轴对称,
∴a=2,b=6,
∴a+b=2+6=8.
C
巩固练习
2. 点P(a+2,2a-5)关于y轴的对称点在第二象限,则a的取值范围是( )
A.a<-2 B.-2<a<????????? C.-????????<a<2 D.a>????????
?
D
解:∵点P(a+2,2a-5)关于y轴的对称点在第二象限,
∴点P在第一象限,
∴????+????>?????????????????>????,
解得a>????????.
?
巩固练习
3. 在坐标平面上有一个轴对称图形,其中A(3,?????????)和B(3,?????????????)是图形上的一对对称点,若此图形上另有一点C(-2,-9),则C点对称点的坐标是( )
A.(-2,1) B.(-2,?????????) C.(?????????,-9) D.(-2,-1)
?
解:∵A(3,?????????)和B(3,?????????????)是图形上的一对对称点,
∴点A与点B关于直线y=-4对称,
∴点C(-2,-9)关于直线y=-4的对称点的坐标为(-2,1).
?
A
巩固练习
4.已知点A(2,0),B(0,4),点P在x轴上,且△PAB的面积为10,则点P的坐标为__________________.
(-3,0)或(7,0)
5.在平面直角坐标系xOy中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点A1(1,2),则点A2的坐标是___________.
(-1,-2)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
巩固练习
6.在如图所示的正方形网格中,每个小正方形的边长都是1,△????????????的顶点都在正方形网格的格点(网格线的交点)上,点A坐标为????,????,点B坐标为????,????.
(1)在正方形网格内,画出平面直角坐标系;
(2)画出△????????????关于y轴对称的△????′????′????′,点????′的坐标为________;
(3)若点????????,????在△????????????的内部,当△????????????当沿y轴翻折后,
点P对应点????′的坐标是___________.
?
?????,????
?
?????,????
?
O
x
y
A
B
C
A′
B′
C′
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
考点分析
例 如图,△A′B′C′是△ABC经过平移得到的,△ABC三个顶点的坐标分别为A(-4,-1),B(-5,-4),C(-1,-3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
考点四 点的平移与坐标变化规律
-2
2
y
4
-4
-6
6
x
2
-2
-4
O
-6
4
6
P
A
B
C
解:(1)∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),
∴平移后对应点的横坐标加6,纵坐标加4,
∴△ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′;
考点分析
(2)写出点A′,C′的坐标;
(3)求△A′B′C′的面积.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
-2
2
y
4
-4
-6
6
x
2
-2
-4
O
-6
4
6
P
A
B
C
(3)如图所示,
S△A′B′C′=3×4-????????×1×3-????????×1×4-????????×2×3=5.5.
?
解:(2)由(1)可知,A′(2,3),C′(5,1);
巩固练习
1.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都减去3,则所得图形与原图形的关系是将原图形( )
A.向上平移3个单位长度 B.向下平移3个单位长度
C.向左平移3个单位长度 D.向右平移3个单位长度
解:将△ABC各点的纵坐标保持不变,横坐标都减去3,所得图形与原图形相比向左平移了3个单位.
C
巩固练习
2. 如图,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(-3,5),B(-4,3),A1(3,3),则点B1的坐标为 ( )
A.(1,2) B.(2,1)
C.(1,4) D.(4,1)
B
巩固练习
3. 已知P(a+1,b-2),Q(4,3)两点.若点P到y轴的距离是3,且PQ∥x轴,求点P的坐标.
解:∵点P到y轴的距离是3,
∴点P的横坐标为3或-3.
又∵PQ∥x轴,
∴点P的纵坐标为3,
∴点P的坐标为(3,3)或(-3,3).
考点分析
4.如图,在方格纸内将△????????????经过一次平移后得到△????′????′????′.图中标出了点C的对应点????′.(利用网格与无刻度直尺画图)
?
(1)画出平移后的△????′????′????′;
(2)利用格点,过点C画一条直线????????,将△????????????分成面积相等的两个三角形;(画出直线????????经过的格点)
(3)在整个平移过程中,线段????????扫过的面积是________.
?
(3)解:线段????????扫过的面积=????×?????????×????????×?????????×????????×????=????????.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
C
B
C′
A′
B′
M
考点分析
例1 如图,在平面直角坐标系中,点A,B的坐标分别是(-2,0),(4,0),现同时将点A,B向上平移2个单位长度,再向右平移2个单位长度,分别得到A,B的对应点C,D.连接AC,BD,CD.
(1)点C的坐标为________,
点D的坐标为______,
四边形ABDC的面积为________.
(0,2)
(6,2)
12
B
D
C
A
x
y
O
考点五 建立适当的平面直角坐标系确定点的坐标
考点分析
(2)在x轴上是否存在一点E,使得△DEC的面积是△DEB面积的2倍?若存在,请求出点E的坐标;若不存在,请说明理由.
解:存在.
设点E的坐标为(x,0),
∵△DEC的面积是△DEB面积的2倍,
∴????????×6×2=2×????????×|4-x|×2,
解得x=1或x=7,
∴点E的坐标为(1,0)或(7,0).
?
B
D
C
A
x
y
O
考点分析
①当表示政府广场的点的坐标为(0,0),表示庐江汽车站的点的坐标为(﹣2,﹣3)时,表示周瑜文化园的点的坐标为(6,﹣4);②当表示政府广场的点的坐标为(0,0),表示庐江汽车站的点的坐标为(﹣4,﹣6)时,表示周瑜文化园的点的坐标为(12,﹣8);③当表示政府广场的点的坐标为(1,1),表示庐江汽车站的点的坐标为(﹣3,﹣5)时,表示周瑜文化园的点的坐标为(13,﹣7);④当表示政府广场的点的坐标为(1.5,1.5)表示庐江汽车站的点的坐标为(﹣4.5,﹣7.5)时,表示周瑜文化园的点的坐标为(19.5,﹣10.5).
上述结论中,所有正确结论的序号是_______________.
①②③④
例2 如图是庐城一些地点的分布示意图.在图中,分别以向右,向上为x轴,y轴的正方向建立平面直角坐标系,有如下四个结论:
巩固练习
1. 如图所示,在正方形网格中,点A的坐标为(-1,0),点B的坐标为(0,-2),则点C的坐标为( )
A. (1,1) B. (-1 ,-1)
C. (-1,1) D. (1,-1)
解: ∵点A的坐标为(-1,0),点B的坐标为(0,-2),
∴建立平面直角坐标系如图所示.
∴点C的坐标为(1,1).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
x
y
A
C
B
A
巩固练习
2.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的坐标是( )
A. (-2,3) B. (2,-1) C.(-2,-1) D.(-3,2)
O
x
y
B
巩固练习
3. 如图,等边三角形OAB的边长为2,则点B的坐标为( )
A. (1,1) B. (????,1) C.(????,????) D.(1,????)
?
B
O
A
y
x
C
解:如图所示,过点B作BC⊥OA于点C.
∵△OAB是等边三角形,且边长为2,
∴OC=????????OA=1.
在Rt△OBC中,由勾股定理得:
BC=?????????????????????????=?????????????????=????,
∴B的坐标为(1,????).
?
D
巩固练习
4.如图,菱形ABCD的边长为6,∠ABC=45°.
(1)试建立适当的平面直角坐标系表示该菱形并写出其各顶点的坐标.
C
D
A
B
x
y
O
E
解:以点为坐标原点,菱形BC的所在的直线为x轴,BC所在直线的垂线为y轴建立平面直角坐标系,如图,
过点A作????????⊥????????于点????,
∵菱形????????????????的边长为6,∠????????????=????????°,
∵ ????????????+????????????=????????????,
∴ ????????=????????????,
∴????????=????????=????????????????=????×????????=????????,????????=????,
∵????????//????????,
∴????(????????,????????),????(????,????),????(????,????),????(????+????????,????????).
?
巩固练习
(2)若要计算该菱形的面积,你有什么办法?
(2)∵????????⊥????????,????????=????????,????????=????,
∴S菱形????????????????=?????????????????????????
=????????×????×????????=????????.
?
C
D
A
B
x
O
E
y
例 如图,在平面直角坐标系xOy中,横坐标和纵坐标都为整数的点称为整点,观察图中每个正方形(实线)四条边上的整点的个数,假如按如图规律继续画正方形(实线),请你猜测由里向外第2023个正方形(实线)的四条边上的整点共有________个.
解:第1个正方形有4×1=4个整数点;
第2个正方形有4×2=8个整数点;
第3个正方形有4×3=12个整数点;
…
第n个正方形有4n个整数点;
所以第2023个正方形有4×2023=8092个整数点.
考点六 点的坐标变化规律探索问题
考点分析
8092
巩固练习
1. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动 , 每移动一个单位 , 得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),……,那么点A2023的坐标为_______________.
????????????????,????
?
2.如图,动点????在平面直角坐标系中按图中箭头所示向运动,第1次从原点运动到点????,????,第2次接着运动到点????,????,第3次接着运动到点????,????,…,按这样的运动规律,经过第2023次运动后,动点????的坐标是_____________.
?
????????????????,????
?
巩固练习
课堂小结
谈谈你本节课的收获是什么?
小结与思考
学习目标
2. 掌握在平面直角坐标系中确定点的坐标描出点的位置的方法;
1. 理解物体的位置变化可以通过确定物体位置的数量变化来说明;
3. 掌握简单的对称图形、图形的平移的坐标关系.
知识框架
物体位置的确定
平面直角坐标系
条件
平面直角坐标系
概念和表示方法
1.区域定位法;2.经纬度定位法;3.方格定位法;
4.行列定位法;5.“方向角+距离”定位法
在平面内,确定一个物体的位置,一般需要两个数据
点的坐标
相关概念
平面直角坐标系;横轴与纵轴;原点;坐标;象限
各象限内点的坐标特征
第一象限:(+,+);第二象限:(-,+)第三象限:(-,-);第四象限:(+,-)
坐标轴上点坐标的特征
x轴上的点,表示为(x,0);
y轴上的点,表示为(0,y).
图形变换与点的坐标变化规律
轴对称
关于x轴对称的点的坐标特征:“纵”变,“横”不变
关于y轴对称的点的坐标特征:“横”变,“纵”不变
平移
左右平移,横坐标“左加右减”
上下平移,纵坐标“上加下减”
考点分析
考点一 位置的确定
例 如图是小军家与周围地区的行走路线示意图,相对小军家来说:
①小军家北偏东30°的方向上有 ; ②要想确定照相馆的位置,还需要 个数据; ③要确定小军家附近的学校的位置,需要 个数据,分别是 .
照相馆
超市
学校
小军家
30°
照相馆、超市
1
2
方向和距离
巩固练习
1.下列表述中,位置确定的是( )
A.北偏东30° B.东经118°,北纬24°
C.淮海路以北,中山路以南 D.银座电影院第2排
B
2.某班级第4组第5排位置可以用数对(4,5)表示,则数对(2,3)表示的位置是( )
A.第3组第2排 B.第3组第1排 C.第2组第3排 D.第2组第2排
C
巩固练习
3. 如图,点O、M、A、B、C在同一平面内.若规定点A的位置记为(50,20°),点B的位置记为(30,60°),则点C的位置应记为________________.
(34,110°)
巩固练习
4.如图,点P、Q在直线l外,在点O沿直线l从左向右的运动过程中,形成了无数个三角形.
(1)观察这些三角形的周长是如何变化的.
O1
l
O2
O3
P
Q
解:这些三角形的周长先由大变小,然后又由小变大.
巩固练习
(2)这无数个三角形的周长有没有最小值?有没有最大值?如果有,试确定点O的位置.
P
Q
O
l
P′
O1
例 在平面直角坐标系中,
(1)已知点P(a﹣1,3a+6)在y轴上,求点P的坐标;
解:(1)∵点P(a﹣1,3a+6)在y轴上,
∴a﹣1=0,解得a=1,
∴3a+6=3×1+6=9,
∴P(0,9).
考点分析
考点二 平面直角坐标系中点的坐标特征
解:(2)∵AB∥x轴,
∴m=4,
∵点B在第一象限,
∴n>0,
∴m=4,n>0.
考点分析
(2)已知两点A(﹣3,m),B(n,4),若AB∥x轴,点B在第一象限,求m的值,并确定n的取值范围;
解:(3)∵AB=5,A、B的纵坐标都为4,
∴点P到AB的距离为9-4=5,
∴以P、A、B为顶点的三角形的面积:
S=????????×5×5=12.5.
?
考点分析
(3)在(1)(2)的条件下,如果线段AB的长度是5,求以P、A、B为顶点的三角形的面积S.
巩固练习
1.已知点M(1-2m,m-1)在第四象限,则m的取值范围是________.
解:由题意,得?????????????>????,①?????????<????,??②
由①得m<0.5,
由②得m<1,
∴m的取值范围是 m< 0.5.
?
m< 0.5
巩固练习
2.点P(2a﹣1,a+2)在x轴上,则点P的坐标为__________.
解:由题意,得
a+2=0,
解得a=﹣2,
2a﹣1=﹣5,
点P的坐标为(﹣5,0).
(﹣5,0)
巩固练习
3.若点A(6,6),AB∥x轴,且AB=2,则B点坐标为( )
A.(4,6) B.(6,4)或(6,8)
C.(6,4) D.(4,6)或(8,6)
解:∵A(6,6),AB∥x轴,
∴点B的纵坐标为6,
点B在点A的左边时,6﹣2=4,
此时点B的坐标为(4,6),
点B在点A的右边时,6+2=8,
此时,点B的坐标为(8,6),
综上所述,点B的坐标为(4,6)或(8,6).
D
巩固练习
4.如图,点A坐标为(3,0),B是y轴正半轴上一点,AB=5,则点B的坐标为( )
A.(4,0) B.(0,4) C.(0,5) D.(0,????????)
?
解:∵点A坐标为(3,0),B是y轴正半轴上一点,AB=5,
∴OB=?????????????????????????=?????????????????=4
∴点B的坐标为(0,4).
?
O
x
y
A
B
B
巩固练习
5. 已知平面直角坐标系中有一点M(m﹣1,2m+3)
(1)当m为何值时,点M到x轴的距离为1?
(2)当m为何值时,点M到y轴的距离为2?
解:(1)∵|2m+3|=1
2m+3=1或2m+3=﹣1
∴m=﹣1或m=﹣2;
(2)∵|m﹣1|=2
m﹣1=2或m﹣1=﹣2
∴m=3或m=﹣1.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
(2)(1)中的△A'B'D的面积为____.?
考点分析
考点三 关于坐标轴对称的点的坐标特征
例 在平面直角坐标系xOy中,已知A(-1,4),B(4,2),C(-1,0)三点.
(1)点A关于y轴的对称点A′的坐标为 ,点B关于x轴的对称点B′的坐标为_______,线段AC的垂直平分线与y轴的交点D的坐标为_______;?
(1,4)
(4,-2)
(0,2)
O
x
y
解:(2)如图,△A'B'D的面积为
4×6-????????×4×4-????????×1×2-????????×3×6=6.
?
6
B
A
C
A′
B′
D
巩固练习
1.在平面直角坐标系中,点P(a,-6)关于x轴对称点为Q(2,b),则a+b的值为( )
A.﹣8 B.8 C. - 4 D.4
解:∵点P(a, -6)与点Q(2,b)关于x轴对称,
∴a=2,b=6,
∴a+b=2+6=8.
C
巩固练习
2. 点P(a+2,2a-5)关于y轴的对称点在第二象限,则a的取值范围是( )
A.a<-2 B.-2<a<????????? C.-????????<a<2 D.a>????????
?
D
解:∵点P(a+2,2a-5)关于y轴的对称点在第二象限,
∴点P在第一象限,
∴????+????>?????????????????>????,
解得a>????????.
?
巩固练习
3. 在坐标平面上有一个轴对称图形,其中A(3,?????????)和B(3,?????????????)是图形上的一对对称点,若此图形上另有一点C(-2,-9),则C点对称点的坐标是( )
A.(-2,1) B.(-2,?????????) C.(?????????,-9) D.(-2,-1)
?
解:∵A(3,?????????)和B(3,?????????????)是图形上的一对对称点,
∴点A与点B关于直线y=-4对称,
∴点C(-2,-9)关于直线y=-4的对称点的坐标为(-2,1).
?
A
巩固练习
4.已知点A(2,0),B(0,4),点P在x轴上,且△PAB的面积为10,则点P的坐标为__________________.
(-3,0)或(7,0)
5.在平面直角坐标系xOy中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点A1(1,2),则点A2的坐标是___________.
(-1,-2)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
巩固练习
6.在如图所示的正方形网格中,每个小正方形的边长都是1,△????????????的顶点都在正方形网格的格点(网格线的交点)上,点A坐标为????,????,点B坐标为????,????.
(1)在正方形网格内,画出平面直角坐标系;
(2)画出△????????????关于y轴对称的△????′????′????′,点????′的坐标为________;
(3)若点????????,????在△????????????的内部,当△????????????当沿y轴翻折后,
点P对应点????′的坐标是___________.
?
?????,????
?
?????,????
?
O
x
y
A
B
C
A′
B′
C′
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
考点分析
例 如图,△A′B′C′是△ABC经过平移得到的,△ABC三个顶点的坐标分别为A(-4,-1),B(-5,-4),C(-1,-3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
考点四 点的平移与坐标变化规律
-2
2
y
4
-4
-6
6
x
2
-2
-4
O
-6
4
6
P
A
B
C
解:(1)∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),
∴平移后对应点的横坐标加6,纵坐标加4,
∴△ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′;
考点分析
(2)写出点A′,C′的坐标;
(3)求△A′B′C′的面积.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
-2
2
y
4
-4
-6
6
x
2
-2
-4
O
-6
4
6
P
A
B
C
(3)如图所示,
S△A′B′C′=3×4-????????×1×3-????????×1×4-????????×2×3=5.5.
?
解:(2)由(1)可知,A′(2,3),C′(5,1);
巩固练习
1.在平面直角坐标系中,将△ABC各点的纵坐标保持不变,横坐标都减去3,则所得图形与原图形的关系是将原图形( )
A.向上平移3个单位长度 B.向下平移3个单位长度
C.向左平移3个单位长度 D.向右平移3个单位长度
解:将△ABC各点的纵坐标保持不变,横坐标都减去3,所得图形与原图形相比向左平移了3个单位.
C
巩固练习
2. 如图,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(-3,5),B(-4,3),A1(3,3),则点B1的坐标为 ( )
A.(1,2) B.(2,1)
C.(1,4) D.(4,1)
B
巩固练习
3. 已知P(a+1,b-2),Q(4,3)两点.若点P到y轴的距离是3,且PQ∥x轴,求点P的坐标.
解:∵点P到y轴的距离是3,
∴点P的横坐标为3或-3.
又∵PQ∥x轴,
∴点P的纵坐标为3,
∴点P的坐标为(3,3)或(-3,3).
考点分析
4.如图,在方格纸内将△????????????经过一次平移后得到△????′????′????′.图中标出了点C的对应点????′.(利用网格与无刻度直尺画图)
?
(1)画出平移后的△????′????′????′;
(2)利用格点,过点C画一条直线????????,将△????????????分成面积相等的两个三角形;(画出直线????????经过的格点)
(3)在整个平移过程中,线段????????扫过的面积是________.
?
(3)解:线段????????扫过的面积=????×?????????×????????×?????????×????????×????=????????.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
A
C
B
C′
A′
B′
M
考点分析
例1 如图,在平面直角坐标系中,点A,B的坐标分别是(-2,0),(4,0),现同时将点A,B向上平移2个单位长度,再向右平移2个单位长度,分别得到A,B的对应点C,D.连接AC,BD,CD.
(1)点C的坐标为________,
点D的坐标为______,
四边形ABDC的面积为________.
(0,2)
(6,2)
12
B
D
C
A
x
y
O
考点五 建立适当的平面直角坐标系确定点的坐标
考点分析
(2)在x轴上是否存在一点E,使得△DEC的面积是△DEB面积的2倍?若存在,请求出点E的坐标;若不存在,请说明理由.
解:存在.
设点E的坐标为(x,0),
∵△DEC的面积是△DEB面积的2倍,
∴????????×6×2=2×????????×|4-x|×2,
解得x=1或x=7,
∴点E的坐标为(1,0)或(7,0).
?
B
D
C
A
x
y
O
考点分析
①当表示政府广场的点的坐标为(0,0),表示庐江汽车站的点的坐标为(﹣2,﹣3)时,表示周瑜文化园的点的坐标为(6,﹣4);②当表示政府广场的点的坐标为(0,0),表示庐江汽车站的点的坐标为(﹣4,﹣6)时,表示周瑜文化园的点的坐标为(12,﹣8);③当表示政府广场的点的坐标为(1,1),表示庐江汽车站的点的坐标为(﹣3,﹣5)时,表示周瑜文化园的点的坐标为(13,﹣7);④当表示政府广场的点的坐标为(1.5,1.5)表示庐江汽车站的点的坐标为(﹣4.5,﹣7.5)时,表示周瑜文化园的点的坐标为(19.5,﹣10.5).
上述结论中,所有正确结论的序号是_______________.
①②③④
例2 如图是庐城一些地点的分布示意图.在图中,分别以向右,向上为x轴,y轴的正方向建立平面直角坐标系,有如下四个结论:
巩固练习
1. 如图所示,在正方形网格中,点A的坐标为(-1,0),点B的坐标为(0,-2),则点C的坐标为( )
A. (1,1) B. (-1 ,-1)
C. (-1,1) D. (1,-1)
解: ∵点A的坐标为(-1,0),点B的坐标为(0,-2),
∴建立平面直角坐标系如图所示.
∴点C的坐标为(1,1).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
x
y
A
C
B
A
巩固练习
2.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的坐标分别为A(-2,1)和B(-2,-3),那么第一架轰炸机C的坐标是( )
A. (-2,3) B. (2,-1) C.(-2,-1) D.(-3,2)
O
x
y
B
巩固练习
3. 如图,等边三角形OAB的边长为2,则点B的坐标为( )
A. (1,1) B. (????,1) C.(????,????) D.(1,????)
?
B
O
A
y
x
C
解:如图所示,过点B作BC⊥OA于点C.
∵△OAB是等边三角形,且边长为2,
∴OC=????????OA=1.
在Rt△OBC中,由勾股定理得:
BC=?????????????????????????=?????????????????=????,
∴B的坐标为(1,????).
?
D
巩固练习
4.如图,菱形ABCD的边长为6,∠ABC=45°.
(1)试建立适当的平面直角坐标系表示该菱形并写出其各顶点的坐标.
C
D
A
B
x
y
O
E
解:以点为坐标原点,菱形BC的所在的直线为x轴,BC所在直线的垂线为y轴建立平面直角坐标系,如图,
过点A作????????⊥????????于点????,
∵菱形????????????????的边长为6,∠????????????=????????°,
∵ ????????????+????????????=????????????,
∴ ????????=????????????,
∴????????=????????=????????????????=????×????????=????????,????????=????,
∵????????//????????,
∴????(????????,????????),????(????,????),????(????,????),????(????+????????,????????).
?
巩固练习
(2)若要计算该菱形的面积,你有什么办法?
(2)∵????????⊥????????,????????=????????,????????=????,
∴S菱形????????????????=?????????????????????????
=????????×????×????????=????????.
?
C
D
A
B
x
O
E
y
例 如图,在平面直角坐标系xOy中,横坐标和纵坐标都为整数的点称为整点,观察图中每个正方形(实线)四条边上的整点的个数,假如按如图规律继续画正方形(实线),请你猜测由里向外第2023个正方形(实线)的四条边上的整点共有________个.
解:第1个正方形有4×1=4个整数点;
第2个正方形有4×2=8个整数点;
第3个正方形有4×3=12个整数点;
…
第n个正方形有4n个整数点;
所以第2023个正方形有4×2023=8092个整数点.
考点六 点的坐标变化规律探索问题
考点分析
8092
巩固练习
1. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动 , 每移动一个单位 , 得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),……,那么点A2023的坐标为_______________.
????????????????,????
?
2.如图,动点????在平面直角坐标系中按图中箭头所示向运动,第1次从原点运动到点????,????,第2次接着运动到点????,????,第3次接着运动到点????,????,…,按这样的运动规律,经过第2023次运动后,动点????的坐标是_____________.
?
????????????????,????
?
巩固练习
课堂小结
谈谈你本节课的收获是什么?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
