有理数总复习
图片预览





文档简介
课件19张PPT。有 理 数 总 复 习一、有理数的基本概念二、有理数的运算1.负数 2.有理数 3.数轴
4.互为相反数
5.互为倒数
6.有理数的绝对值
7.有理数大小的比较
加、减、乘、除、乘方运算一、有理数的基本概念1.负数:在正数前面加“—”的数;0既不是正数,也不是负数。判断:
1)a一定是正数;
2)-a一定是负数;
3)-(-a)一定大于0;
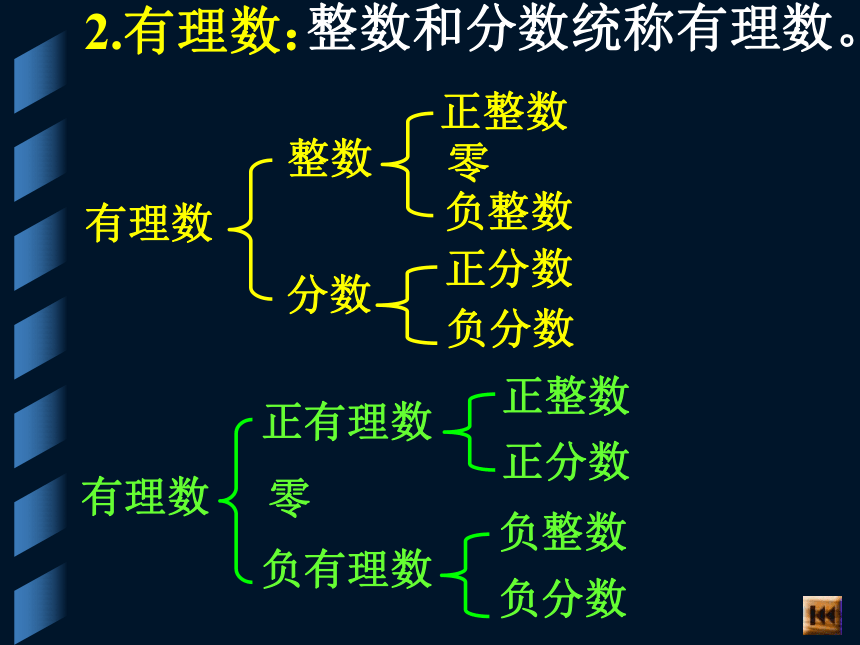
4)0是正整数。××××2.有理数:整数和分数统称有理数。有理数整数分数正整数 零负整数正分数负分数有理数正有理数零负有理数正整数正分数负整数负分数3.数 轴规定了原点、正方向和单位长度的直线.1)在数轴上表示的两个数,
右边的数总比左边的数大;2)正数都大于0,负数都小于0;
正数大于一切负数;3)所有有理数都可以用数轴上
的点表示。4.相反数 只有符号不同的两个数,
其中一个是另一个的相反数。 1)数a的相反数是-a2)0的相反数是0. -22-443)若a、b互为相反数,则a+b=0. (a是任意一个有理数);5.倒 数 乘积是1的两个数互为倒数 .1)a的倒数是 (a≠0); 3)若a与b互为倒数,则ab=1.2)0没有倒数 ;例:下列各数,哪两个数互为倒数?
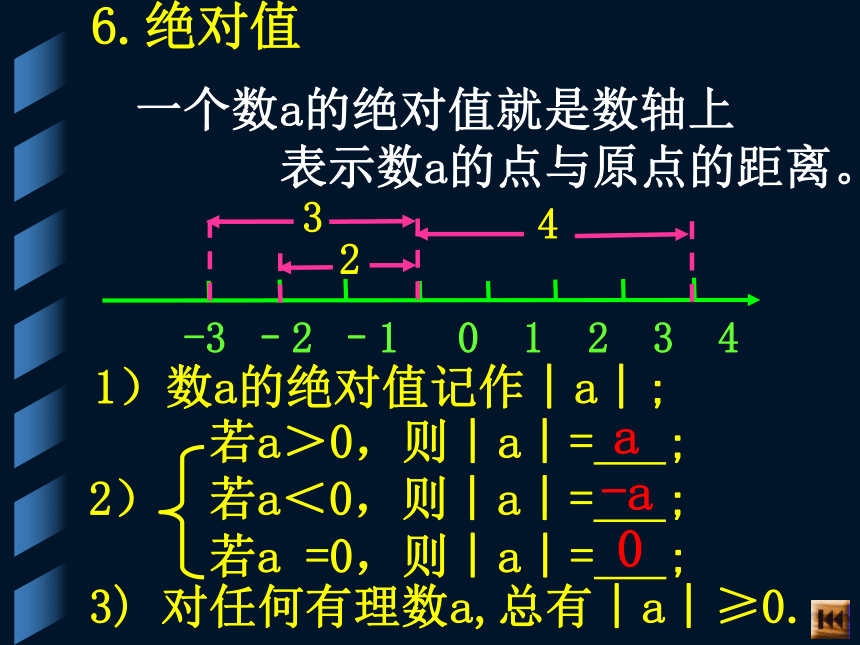
8, ,-1,+(-8),1,6.绝对值一个数a的绝对值就是数轴上
表示数a的点与原点的距离。1)数a的绝对值记作︱a︱; a-a03) 对任何有理数a,总有︱a︱≥0.练习:0-1非正数1,-1±2±4负数非正数0非正数2. 已知x,y互为相反数,a,b互为倒 数,
m的绝对值为3。 求代数式 4(x+y)-ab+m2的值 解:∵x、y互为相反数,a、b互为倒数,
m的绝对值为3∴x+y=0,ab=1,m=±3 即 m2=(±3)2=9
∴ 4(x+y)-ab+m2 =4×0-1+9 =8 若a>0,b<0,︱a︱>︱b︱, 则a+b=1)用数学语言描述有理数加法法则:①同号相加:
若a>0,b>0,则a+b=若a<0,b<0,则a+b=若a>0,b<0,︱a︱<︱b︱,
则a+b=②异号相加③与0相加若a、b互为相反数,则a+b=a是任一个有理数,则a+0=︱a︱+︱b︱-︱a︱-︱b︱(︱b︱-︱a︱)0a(︱a︱+︱b︱)-2)有理数减法法则 减去一个数,
等于加上这个数的相反数.
即 a-b=a+(-b)例:分别求出数轴上两点间的距离:
①表示2的点与表示-7的点;
②表示-3的点与表示-1的点。解:①︱2-(-7)︱=︱2+7︱=︱9︱=9
②︱-3-(-1)︱=︱-3+1︱=︱-2︱=2用数学语言描述有理数乘法法则:①同号相乘
若a>0,b>0,则 ab=︱a︱×︱b︱若a<0,b<0,则 ab=︱a︱×︱b︱②异号相乘
若a>0,b<0,则 ab=若a<0,b>0,则 ab=︱a︱×︱b︱︱a︱×︱b︱③数与0相乘a为任何有理数,则 a×0=0++--2) 若 20, X-6<0∴ |X-2|-|X-6|=X-2-[-(X-6)]
=X-2+X-6
=2X-81) 若m
即a÷b=a× (b≠0)② 两数相除,同号得正,异号得负,
并把绝对值相除;
0除以任何一个不等于0的数,都
得0.5)有理数的乘方 ①求n个相同因数的积的运算,叫做乘方。②正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数. 小测
1.( )和( )统称为有理数
2.最小的正整数是( ).最小的非负整数( ).
3.(1)-9.3,(2) 6,(3)-7—,(4)0 (5)-100
(6)3.25,(7)-2.5,(8)0.01,(9)+65(10) —
整数集合( ),负整数集合( ),负分数集
合( ),负数集合( ),非正整数集合( ).
4.与原点距离为4的数是( )
5.a=-13,则-a=( ),-a=-b,则a=( )133100若a是负数,则-a是( ).若-a是负数,则
a是( ).
6.a-b的相反数是( ).5+a的相反数是( )
-(-8.09)的相反数是( ).
7.绝对值最小的数是( ).|3-π|=( ),
|a|=3,a=( ).|a|=a,则a的取值范围?
|a|=-a,则a的取值范围?
|a|≥a,则a的取值范围?
8.|a|=4, |b|=2 求a+b的值
9. 2< x<6 |x-2|-|x-6|=( )
10. 若a<b<0 化简|a-b|-|a|的值
11. 比较大小 - -0.273
12.若x<0 则|x-(-x)|=( )3
11认真.严谨.
善思.好问.
4.互为相反数
5.互为倒数
6.有理数的绝对值
7.有理数大小的比较
加、减、乘、除、乘方运算一、有理数的基本概念1.负数:在正数前面加“—”的数;0既不是正数,也不是负数。判断:
1)a一定是正数;
2)-a一定是负数;
3)-(-a)一定大于0;
4)0是正整数。××××2.有理数:整数和分数统称有理数。有理数整数分数正整数 零负整数正分数负分数有理数正有理数零负有理数正整数正分数负整数负分数3.数 轴规定了原点、正方向和单位长度的直线.1)在数轴上表示的两个数,
右边的数总比左边的数大;2)正数都大于0,负数都小于0;
正数大于一切负数;3)所有有理数都可以用数轴上
的点表示。4.相反数 只有符号不同的两个数,
其中一个是另一个的相反数。 1)数a的相反数是-a2)0的相反数是0. -22-443)若a、b互为相反数,则a+b=0. (a是任意一个有理数);5.倒 数 乘积是1的两个数互为倒数 .1)a的倒数是 (a≠0); 3)若a与b互为倒数,则ab=1.2)0没有倒数 ;例:下列各数,哪两个数互为倒数?
8, ,-1,+(-8),1,6.绝对值一个数a的绝对值就是数轴上
表示数a的点与原点的距离。1)数a的绝对值记作︱a︱; a-a03) 对任何有理数a,总有︱a︱≥0.练习:0-1非正数1,-1±2±4负数非正数0非正数2. 已知x,y互为相反数,a,b互为倒 数,
m的绝对值为3。 求代数式 4(x+y)-ab+m2的值 解:∵x、y互为相反数,a、b互为倒数,
m的绝对值为3∴x+y=0,ab=1,m=±3 即 m2=(±3)2=9
∴ 4(x+y)-ab+m2 =4×0-1+9 =8 若a>0,b<0,︱a︱>︱b︱, 则a+b=1)用数学语言描述有理数加法法则:①同号相加:
若a>0,b>0,则a+b=若a<0,b<0,则a+b=若a>0,b<0,︱a︱<︱b︱,
则a+b=②异号相加③与0相加若a、b互为相反数,则a+b=a是任一个有理数,则a+0=︱a︱+︱b︱-︱a︱-︱b︱(︱b︱-︱a︱)0a(︱a︱+︱b︱)-2)有理数减法法则 减去一个数,
等于加上这个数的相反数.
即 a-b=a+(-b)例:分别求出数轴上两点间的距离:
①表示2的点与表示-7的点;
②表示-3的点与表示-1的点。解:①︱2-(-7)︱=︱2+7︱=︱9︱=9
②︱-3-(-1)︱=︱-3+1︱=︱-2︱=2用数学语言描述有理数乘法法则:①同号相乘
若a>0,b>0,则 ab=︱a︱×︱b︱若a<0,b<0,则 ab=︱a︱×︱b︱②异号相乘
若a>0,b<0,则 ab=若a<0,b>0,则 ab=︱a︱×︱b︱︱a︱×︱b︱③数与0相乘a为任何有理数,则 a×0=0++--2) 若 2
=X-2+X-6
=2X-81) 若m
即a÷b=a× (b≠0)② 两数相除,同号得正,异号得负,
并把绝对值相除;
0除以任何一个不等于0的数,都
得0.5)有理数的乘方 ①求n个相同因数的积的运算,叫做乘方。②正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数. 小测
1.( )和( )统称为有理数
2.最小的正整数是( ).最小的非负整数( ).
3.(1)-9.3,(2) 6,(3)-7—,(4)0 (5)-100
(6)3.25,(7)-2.5,(8)0.01,(9)+65(10) —
整数集合( ),负整数集合( ),负分数集
合( ),负数集合( ),非正整数集合( ).
4.与原点距离为4的数是( )
5.a=-13,则-a=( ),-a=-b,则a=( )133100若a是负数,则-a是( ).若-a是负数,则
a是( ).
6.a-b的相反数是( ).5+a的相反数是( )
-(-8.09)的相反数是( ).
7.绝对值最小的数是( ).|3-π|=( ),
|a|=3,a=( ).|a|=a,则a的取值范围?
|a|=-a,则a的取值范围?
|a|≥a,则a的取值范围?
8.|a|=4, |b|=2 求a+b的值
9. 2< x<6 |x-2|-|x-6|=( )
10. 若a<b<0 化简|a-b|-|a|的值
11. 比较大小 - -0.273
12.若x<0 则|x-(-x)|=( )3
11认真.严谨.
善思.好问.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
