3.1 函数的表示法 课件(共20张PPT)
文档属性
| 名称 | 3.1 函数的表示法 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 674.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
函数的表示法
温故知新
函数三要素: 定义域 、 对应关系和值域
函数三种表示法: 图象法 、 列表法和解析法
高中数学
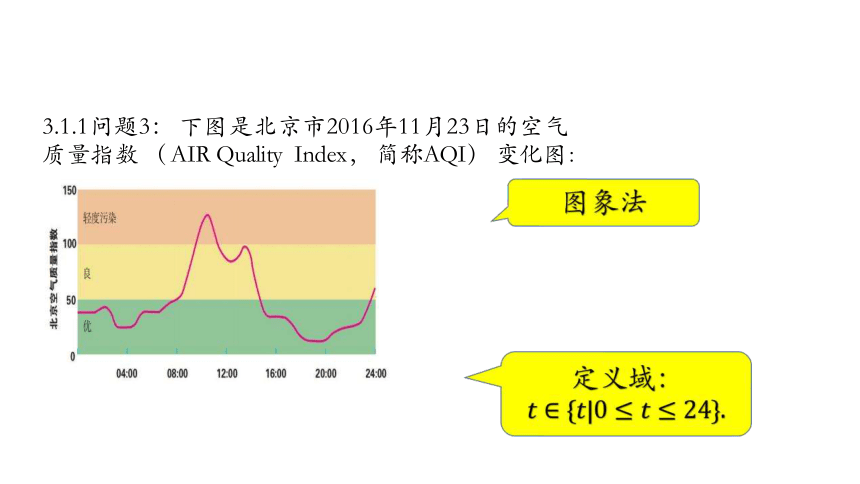
3.1.1问题3: 下图是北京市2016年11月23日的空气 质量指数 ( AIR Quality Index, 简称AQI) 变化图:
高中数学
图象法: 以自变量 的取值为横坐标, 对应的函数值 为 纵坐标, 在平面直角坐标系中描出各个点, 这些点构成 了函数的图象, 这种用图象表示两个变量之间函数关系 的方法叫做图象法 .
自变量 的取值范围为函数的定义域.
高中数学
定义域:
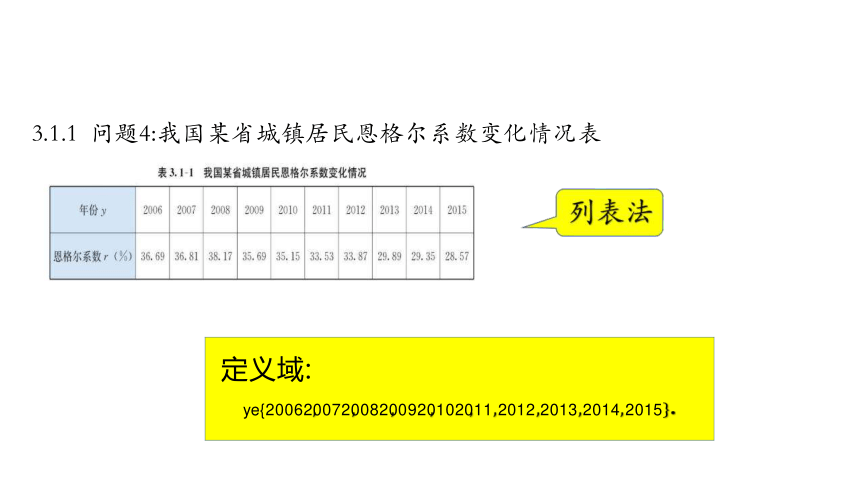
3.1.1 问题4:我国某省城镇居民恩格尔系数变化情况表
ye{200620072008200920102011 2012 2013 2014 2015
高中数学
列表法: 列 一 个两行多列的表格, 第 一行是自变量的取值 , 第 二行是对应的函数值, 这种用表格来表示两个变量之间的 函数关系的方法叫做列表法 .
第 一行自变量 的取值范围为函数的定义域.
高中数学
3.1.1问题1: 某 “ 复兴号 ” 高速列车加速到350km/h后保持匀速运 行半小时. 这段时间内, 列车行进的路程S(单位: k m ) 与运行 时间t(单位: h) 的关系可以表示为:
= 350, ∈ { |0 ≤ ≤ 0.5}.
解析法
高中数学
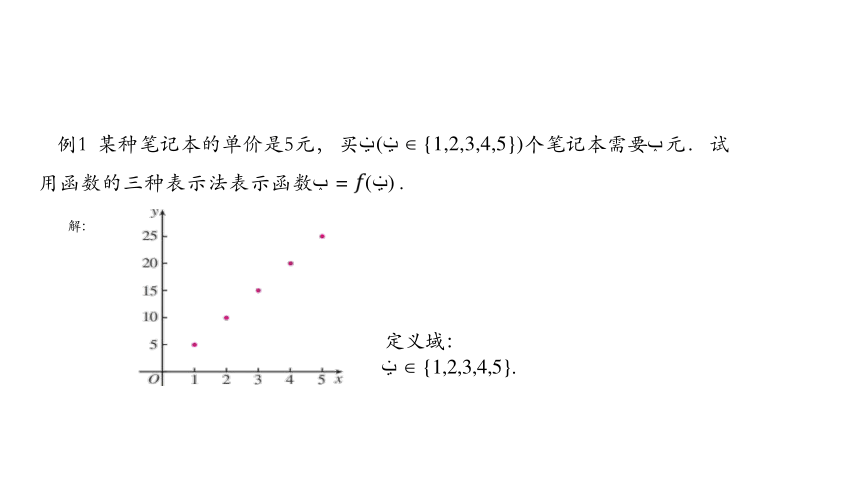
例1 某种笔记本的单价是5元, 买 ( ∈ {1,2,3,4,5})个笔记本需要 元. 试
用函数的三种表示法表示函数 = ( ) .
解: 用列表法可将函数 = ( )表示为:
其中定义域: ∈ {1,2,3,4,5}.
高中数学
例1 某种笔记本的单价是5元, 买 ( ∈ {1,2,3,4,5})个笔记本需要 元. 试
用函数的三种表示法表示函数 = ( ) .
定义域:
∈ {1,2,3,4,5}.
高中数学
解:
例1 某种笔记本的单价是5元, 买 ( ∈ {1,2,3,4,5})个笔记本需要 元. 试
用函数的三种表示法表示函数 = ( ) .
【分析】由列表的过程可知, 在得到表中第二行钱数 的值的时候, 也是需 要通过题意简单计算的. 其所用的计算式为 = 5, ∈ ,4,3,2,1{}5.
解: 这个函数的定义域是数集{1,2,3,4,5},
用解析法可将函数 = ( )表示为:
= 5, ∈ {1,2,3,4,5}.
高中数学
提问1: 函数的三种表示法各自的特点是什么?
解析法: 简明 、 抽象 、 有规律.
图象法: 直观 、 趋势 、 不精准.
列表法: 直观 、 离散.
高中数学
解: 由绝对值的概念可得:
y = 0,
所以, 函数图象为:
高中数学
0
<
x
, x
x,
x
-
ìí
例2 画出函数y = |x |的图象. 分段函数
以数化形
分段函数: 函数定义域分成若干区间段,
在各个区间段内, 函数有不同的对应关系.
分段函数是 一 个函数, 不是几个函数, 分 段函数的定义域是各段函数定义域的并集.
高中数学
= | |
< 0时, 自变量 变大时, 应变量 变小.
> 0时, 自变量 变大时, 应变量 变大.
高中数学
解析法抽象而精准,
图象法直观而形象,
二者相辅相成, 能更 好的理解这 一 函数,
这就是所谓数形结合.
例3 给定函数 ( ) = + ,1 ( ) = ( + 1) , ∈ R,
(1 ) 在同 一 坐标系中画出 ( ), ( )的图象;
(2) ∈ R, 用 ( )表示 ( ), ( )中的较大者, 记为
M (x) =max{f(x), g(x)}.
请分别用图象法和解析法表示函数M( ).
高中数学
解:( 1)
(2)
高中数学
(2) 解析法: =(x +1)2 =x +1
祆x =- 1
或
铑y =0
ì
(x +1)2 , x - 1,
x +1,- 10.
\ M (x) =
í
x =0
y =1
高中数学
:眄
解析法 列表法
图象法
1. 简明 2.抽象 直观
1. 直观形象
2. 变化趋势
1.有规律 2. 不直观 1. 离散 2. “ 少 ”
1. 不精准
2. 不全面
课堂小结:
1. 内容上:
高中数学
课堂小结:
2. 思想方法上:
数形结合
以形化数+以数辅形.
高中数学
四、 课后作业
某市 “ 招手即停 ”公共汽车的票价按下列规则制定:
( 1 ) 5 k m以内(含5 k m ) , 票价2元;
( 2 ) 5 k m以上, 每增加5 k m , 票价增加1元 ( 不足5 k m 的按5 k m 计算) .
如果某条线路的总里程为20 k m , 请根据题意, 写出票价与里程之间的函数解析
式, 并画出函数的图象 .
高中数学
函数的表示法
温故知新
函数三要素: 定义域 、 对应关系和值域
函数三种表示法: 图象法 、 列表法和解析法
高中数学
3.1.1问题3: 下图是北京市2016年11月23日的空气 质量指数 ( AIR Quality Index, 简称AQI) 变化图:
高中数学
图象法: 以自变量 的取值为横坐标, 对应的函数值 为 纵坐标, 在平面直角坐标系中描出各个点, 这些点构成 了函数的图象, 这种用图象表示两个变量之间函数关系 的方法叫做图象法 .
自变量 的取值范围为函数的定义域.
高中数学
定义域:
3.1.1 问题4:我国某省城镇居民恩格尔系数变化情况表
ye{200620072008200920102011 2012 2013 2014 2015
高中数学
列表法: 列 一 个两行多列的表格, 第 一行是自变量的取值 , 第 二行是对应的函数值, 这种用表格来表示两个变量之间的 函数关系的方法叫做列表法 .
第 一行自变量 的取值范围为函数的定义域.
高中数学
3.1.1问题1: 某 “ 复兴号 ” 高速列车加速到350km/h后保持匀速运 行半小时. 这段时间内, 列车行进的路程S(单位: k m ) 与运行 时间t(单位: h) 的关系可以表示为:
= 350, ∈ { |0 ≤ ≤ 0.5}.
解析法
高中数学
例1 某种笔记本的单价是5元, 买 ( ∈ {1,2,3,4,5})个笔记本需要 元. 试
用函数的三种表示法表示函数 = ( ) .
解: 用列表法可将函数 = ( )表示为:
其中定义域: ∈ {1,2,3,4,5}.
高中数学
例1 某种笔记本的单价是5元, 买 ( ∈ {1,2,3,4,5})个笔记本需要 元. 试
用函数的三种表示法表示函数 = ( ) .
定义域:
∈ {1,2,3,4,5}.
高中数学
解:
例1 某种笔记本的单价是5元, 买 ( ∈ {1,2,3,4,5})个笔记本需要 元. 试
用函数的三种表示法表示函数 = ( ) .
【分析】由列表的过程可知, 在得到表中第二行钱数 的值的时候, 也是需 要通过题意简单计算的. 其所用的计算式为 = 5, ∈ ,4,3,2,1{}5.
解: 这个函数的定义域是数集{1,2,3,4,5},
用解析法可将函数 = ( )表示为:
= 5, ∈ {1,2,3,4,5}.
高中数学
提问1: 函数的三种表示法各自的特点是什么?
解析法: 简明 、 抽象 、 有规律.
图象法: 直观 、 趋势 、 不精准.
列表法: 直观 、 离散.
高中数学
解: 由绝对值的概念可得:
y = 0,
所以, 函数图象为:
高中数学
0
<
x
, x
x,
x
-
ìí
例2 画出函数y = |x |的图象. 分段函数
以数化形
分段函数: 函数定义域分成若干区间段,
在各个区间段内, 函数有不同的对应关系.
分段函数是 一 个函数, 不是几个函数, 分 段函数的定义域是各段函数定义域的并集.
高中数学
= | |
< 0时, 自变量 变大时, 应变量 变小.
> 0时, 自变量 变大时, 应变量 变大.
高中数学
解析法抽象而精准,
图象法直观而形象,
二者相辅相成, 能更 好的理解这 一 函数,
这就是所谓数形结合.
例3 给定函数 ( ) = + ,1 ( ) = ( + 1) , ∈ R,
(1 ) 在同 一 坐标系中画出 ( ), ( )的图象;
(2) ∈ R, 用 ( )表示 ( ), ( )中的较大者, 记为
M (x) =max{f(x), g(x)}.
请分别用图象法和解析法表示函数M( ).
高中数学
解:( 1)
(2)
高中数学
(2) 解析法: =(x +1)2 =x +1
祆x =- 1
或
铑y =0
ì
(x +1)2 , x - 1,
x +1,- 1
\ M (x) =
í
x =0
y =1
高中数学
:眄
解析法 列表法
图象法
1. 简明 2.抽象 直观
1. 直观形象
2. 变化趋势
1.有规律 2. 不直观 1. 离散 2. “ 少 ”
1. 不精准
2. 不全面
课堂小结:
1. 内容上:
高中数学
课堂小结:
2. 思想方法上:
数形结合
以形化数+以数辅形.
高中数学
四、 课后作业
某市 “ 招手即停 ”公共汽车的票价按下列规则制定:
( 1 ) 5 k m以内(含5 k m ) , 票价2元;
( 2 ) 5 k m以上, 每增加5 k m , 票价增加1元 ( 不足5 k m 的按5 k m 计算) .
如果某条线路的总里程为20 k m , 请根据题意, 写出票价与里程之间的函数解析
式, 并画出函数的图象 .
高中数学
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
