人教A版(2019)高数必修第一册 5.6 函数y=Asin(ωx+φ)的图象 课件(共37张PPT)
文档属性
| 名称 | 人教A版(2019)高数必修第一册 5.6 函数y=Asin(ωx+φ)的图象 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 302.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 09:56:19 | ||
图片预览







文档简介
(共37张PPT)
函数 y =Asin(ωx+φ)的图象(2)
高中数学
复习回顾
问题 1:研究参数A , , 对函数y = Asin( ωx+φ)图象的影
响是按怎样的思路展开研究的?
从局部到整体 .
问题 2:研究参数 对函数y = sin(x+φ)图象的影响时 ,是怎
样进行研究的?
y = sin x 与 y = sin(x + 特殊到 一 = sin x 与 y = sin(x + )
高中数学
y
般
6
π)
从
问题 3:类比参数 对函数y = sin(x+φ)图象影响的研究
过程,你计划怎样研究参数ω( ω>0)对函数y = sin( ωx+φ) 图象的影响?
从特殊到 一般 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
追问:( 1 ) 结合筒车模型,ω 取不同值表示什么含义?
o取不同值表示质点以不同的角速度做匀速圆周运动 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
追问:( 2 ) 若给 ω 赋特殊值, 你认为给 φ 取哪个特殊
值比较合适?
不妨设 = , 固定 的值 , 改变参数ω( ω>0),研究函
数y = sin( ωx+ )与y = sin(x+ )图象之间的变换关系 .
高中数学
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
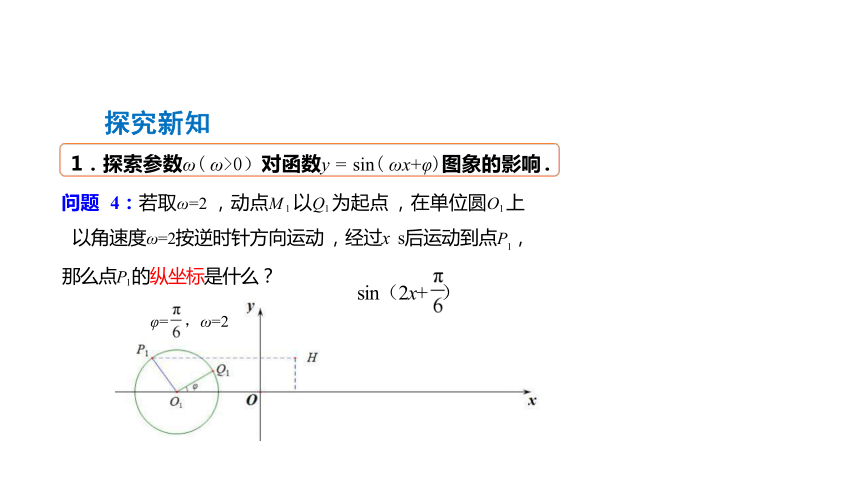
问题 4:若取ω=2 ,动点M 1 以Q1 为起点 ,在单位圆O1 上
以角速度ω=2按逆时针方向运动 ,经过x s后运动到点P1,
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
那么点P1 的纵坐标是什么?
φ= ,ω=2
sin(2x+ )
探究新知
高中数学
φ= ,ω=2
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
追问:此时 ,以(x , y)为坐标描点H ,点H 的轨迹对应的
y = sin(2x+ )
函数解析式是什么?
探究新知
高中数学
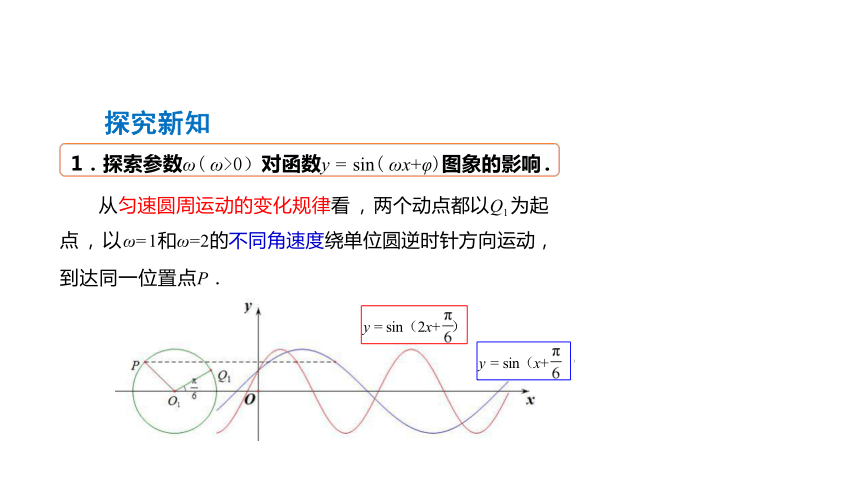
问题 s:函数y = sin(2x+ )与y = sin(x+ )的图象之间存
在怎样的变换关系?你能从质点的匀速圆周运动规律和 函数图象上点的坐标变化的角度进行解释吗?
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x+
探究新知
高中数学
)
从匀速圆周运动的变化规律看 , 两个动点都以Q1 为起
点 , 以 ω= 1和ω=2的不同角速度绕单位圆逆时针方向运动, 到达同一位置点P .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x+
探究新知
高中数学
)
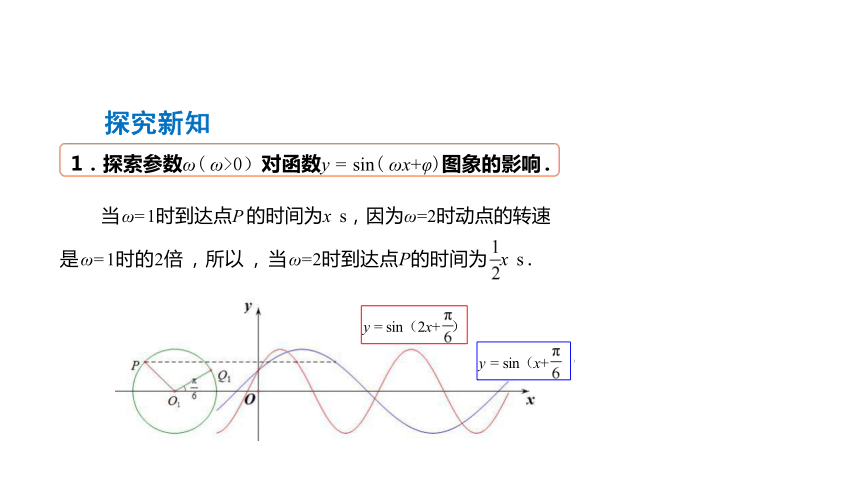
当 ω= 1时到达点P 的时间为x s,因为ω=2时动点的转速
是 ω= 1时的2倍 ,所以 , 当 ω=2时到达点P的时间为 x s .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x+
探究新知
高中数学
)
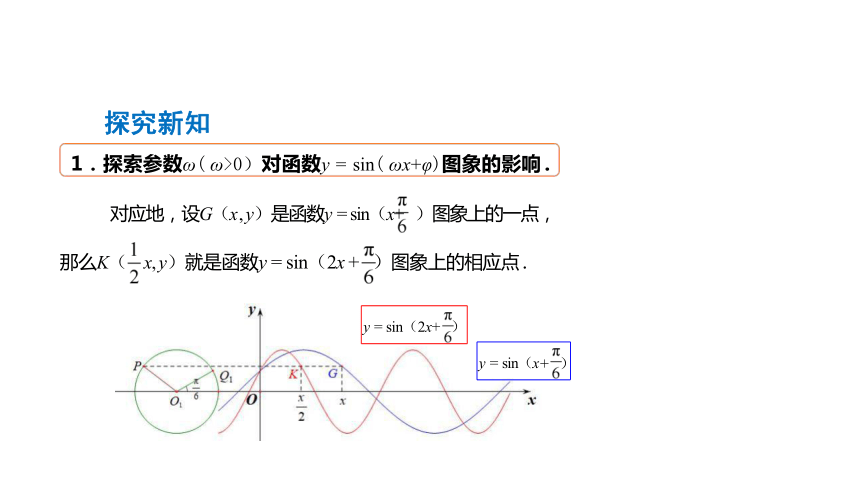
对应地,设G(x , y)是函数y = sin(x+ )图象上的一点,
那么K( x, y)就是函数y = sin(2x + )图象上的相应点 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x
探究新知
高中数学
+ )
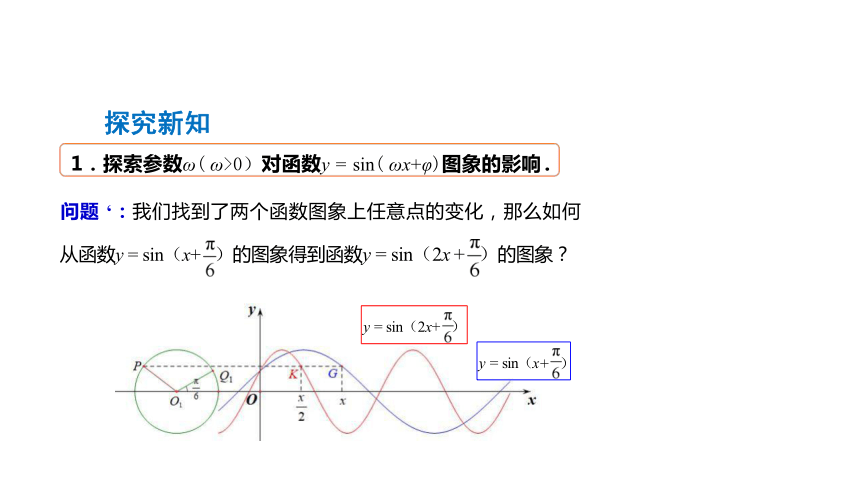
问题 ‘:我们找到了两个函数图象上任意点的变化,那么如何
从函数y = sin(x+ )的图象得到函数y = sin(2x + )的图象?
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x
探究新知
高中数学
+ )
总结:函数y = sin(2x + )的图象是把函数y = sin(x + )的图象
上所有点的横坐标缩短到原来的 (纵坐标不变)得到的 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x
探究新知
高中数学
+ )
总结:函数y = sin(2x + )的图象是把函数y = sin(x + )的图象
上所有点的横坐标缩短到原来的 (纵坐标不变)得到的 . 并且 , y = sin(2x + )的周期为π , 是y = sin(x+ )的周期的 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
问题 7:如果ω取 ,3, 时,对应的函数y = sin( ωx+ )的图
象与y= sin(x+ )的图象之间存在怎样的变换关系?
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
分析: 当 ω= 时 ,动点的转速是ω=1时的 , 以Q1 为起点 ,到
达点P 的时间是ω=1时的2倍 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
E(2x, y)
y = sin( x+ )
6
π
2
1
G(x, y)
y = sin(x+ )
6
π
探究新知
高中数学
分析 :所以把y= sin(x+ )图象上所有点的横坐标伸长到原来
的2倍(纵坐标不变),就得到y= sin( x+ )的图象 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
E(2x, y)
y = sin( x+ )
6
π
2
1
G(x, y)
y = sin(x+ )
6
π
探究新知
高中数学
分析 :所以把y= sin(x+ )图象上所有点的横坐标伸长到原来
的2倍(纵坐标不变),就得到y= sin( x+ )的图象 .
并且,y = sin( x+ )的周期是4π , 是y = sin(x+ )的周期的2倍 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
总结:一般地,函数y = sin( ωx+φ)的周期是 , 把y = sin(x+φ)
图象上所有点的横坐标缩短(当ω>1时)或伸长(当0< ω<1时) 到原来的 倍(纵坐标不变),就得到 y = sin( ωx+φ)的图象 .
问题 8:结合上面的研究过程 ,你能给出ω( ω>0)的变化对函
数y = sin( ωx+φ)图象影响的一般化结论吗?
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
问题 9:( 1)结合筒车模型 , A取不同值表示什么含义?
分析: A代表质点做匀速圆周运动的运动半径 , A取不同值表
示质点以不同的运动半径做匀速圆周运动 .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
高中数学
问题 9:(2)若给 A赋特殊值,你认为给 ,ω取哪个特殊值比
较合适?
分析:为了研究方便,不妨设 = , ω=2 ,固定 , ω的值 ,改
变参数A(A>0),研究函数y = Asin(2x+ )与y = sin(2x+ )的图象 之间的变换关系 .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
高中数学
问题 10: 函数y = 2sin(2x+ )与y = sin(2x+ )的图象之间
存在怎样的变换关系?你能从质点的匀速圆周运动规律和函 数图象上点的坐标变化的角度进行解释吗?
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
y = 2sin(2x+ )
y = sin(2x+ )
高中数学
分析:在以O1 为圆心,半径分别为 1 和 2 的圆上,两个动点分
别以Q1 和T1 为起点 , ω=2的转速经过x s后分别到达圆周上的点 P 和点T ,易得点T 的纵坐标是点P 的纵坐标的 2 倍 .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
y = 2sin(2x+ )
y = sin(2x+ )
高中数学
2y
y
分析:对应地,设K(x , y)是函数y = sin(2x+ )图象上的一点,
那么N(x , 2y)就是函数y = 2sin(2x + )图象上的相应点 .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
y = 2sin(2x+ )
y = sin(2x+ )
高中数学
2y
y
问题 11:我们找到了两个函数图象上任意点的变化 ,那么如何
从函数y = sin(2x+ )的图象得到函数y = 2sin(2x + )的图象?
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
y = 2sin(2x+ )
y = sin(2x+ )
高中数学
2y
y
总结: 函数y = 2sin(2x + )的图象是把函数y = sin(2x+ )的图
象上所有点的纵坐标伸长到原来的2倍(横坐标不变)得到的 .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
y = 2sin(2x+ )
y = sin(2x+ )
高中数学
2y
y
问题 12:如果A取 ,3 , 时,对应的函数y = Asin(2x+ )
的 图 象 与 y= sin(2x+ )的 图 象 之 间 存 在 怎 样 的 变 换 关 系? 你能给出 A(A>0)的变化对函数y = Asin( ωx+φ)图象 影响的一般化结论吗?
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
高中数学
总结: 函数y = Asin( ωx+φ)的图象 , 可以看作是把函数
y = sin( ωx+φ)的图象上所有点的纵坐标伸长(当 A>1时) 或缩短(当0<A<1时)为原来的 A倍(横坐标不变)而得 到.从而 ,函数y = Asin( ωx+φ)的值域是[-A, A],最大值 是A ,最小值是-A .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
高中数学
问题 13:我们分别研究了三个参数对函数y = Asin( ωx+φ)图
象的影响.并按照路线y = sin x y = sin(x+ ) y = sin(2x+ ) y = 2sin(2x+ ),你能总结一下这个变换过程吗?
3 .总结从正弦曲线出发 ,通过图象变换得到y= Asin( ωx+φ)的图象 .
探究新知
高中数学
y = sin(2x+ 伸长到原来的2 = 2sin(2x+ )
高中数学
6
π
y
倍
变
坐
不
纵
6 (横坐标
π)所有点的
π 所有点的横坐标缩短到原来的 1
y = sin(x+ ) 2
6 (纵坐标不变).
3 .总结从正弦曲线出发 ,通过图象变换得到y= Asin( ωx+φ)的图象 .
所有点向左平移 π 个单位长度 . y = sin x 6
y = sin(x+ )
y = sin(2x+ )
探究新知
追问: 你能总结一下从正弦函数y = sin x图象出发 ,通过图
象变换得到函数y = Asin( ωx+φ)(A>0,ω>0)图象的过程与 方法吗?
请填写在教科书第 236 页的表格中 .
3 .总结从正弦曲线出发 ,通过图象变换得到y= Asin( ωx+φ)的图象 .
探究新知
高中数学
y = sin(x+ = sin( x+Q)
y = sin( x+ )= Asin( x+Q)
高中数学
变
y
短
不
缩
(横坐标
>1时) 或
倍
A
) 为原来的A
坐标伸长(当
时
纵
(当0
Q)所
>
变)
y
长
不
伸
(纵坐标
1时)或
的
(
来
短
时)到原
横坐标缩
(
Q
3 .总结从正弦曲线出发 ,通过图象变换得到y= Asin( ωx+φ)的图象 .
所有点向左(当φ>0时)或向右(当φ<0时)
y = sin(x+Q)
平移 φ 个单位长度 .
探究新知
y = sin x
学以致用
练习: 已知函数y = 3sin x的图象为C .
(1) 为了得到函数y = 3sin 2x的图象 ,只要把C 上所有的点
(A)横坐标伸长到原来的2倍 ,纵坐标不变
(B)横坐标缩短到原来的 ,纵坐标不变
(C)纵坐标伸长到原来的2倍 ,横坐标不变
(D)纵坐标缩短到原来的 ,横坐标不变
高中数学
学以致用
练习: 已知函数y = 3sin x的图象为C .
(2) 为了得到函数y= 4sin x的图象 ,只要把C 上所有的点
(A)横坐标伸长到原来的 倍 ,纵坐标不变
(B)横坐标缩短到原来的 ,纵坐标不变
(C)纵坐标伸长到原来的 倍 ,横坐标不变
(D)纵坐标缩短到原来的 ,横坐标不变
高中数学
参数A , , 对
— 函数y = Asin( ωx +φ)
图象的影响
函数
y = Asin( x + )
函数 y = Asin( x + )的性质
现实世界中的
匀速圆周运动
课堂小结
高中数学
重点研究了 ,A 对函数 y = Asin( x + )图象的影响;
进 一 步体会从特殊到 一般 、 数形结合的思想方法;
发展数学抽象 、 逻辑推理以及直观想象的学科素养 .
课堂小结
高中数学
参数A , , 对
— 函数y = Asin( ωx +φ)
图象的影响
函数 y = Asin( x + )
的简单应用
现实世界中的
匀速圆周运动
函
y = Asi
x + )
数
n (
函数 y = Asin( x + )的性质
课堂小结
高中数学
函数 y =Asin(ωx+φ)的图象(2)
高中数学
复习回顾
问题 1:研究参数A , , 对函数y = Asin( ωx+φ)图象的影
响是按怎样的思路展开研究的?
从局部到整体 .
问题 2:研究参数 对函数y = sin(x+φ)图象的影响时 ,是怎
样进行研究的?
y = sin x 与 y = sin(x + 特殊到 一 = sin x 与 y = sin(x + )
高中数学
y
般
6
π)
从
问题 3:类比参数 对函数y = sin(x+φ)图象影响的研究
过程,你计划怎样研究参数ω( ω>0)对函数y = sin( ωx+φ) 图象的影响?
从特殊到 一般 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
追问:( 1 ) 结合筒车模型,ω 取不同值表示什么含义?
o取不同值表示质点以不同的角速度做匀速圆周运动 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
追问:( 2 ) 若给 ω 赋特殊值, 你认为给 φ 取哪个特殊
值比较合适?
不妨设 = , 固定 的值 , 改变参数ω( ω>0),研究函
数y = sin( ωx+ )与y = sin(x+ )图象之间的变换关系 .
高中数学
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
问题 4:若取ω=2 ,动点M 1 以Q1 为起点 ,在单位圆O1 上
以角速度ω=2按逆时针方向运动 ,经过x s后运动到点P1,
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
那么点P1 的纵坐标是什么?
φ= ,ω=2
sin(2x+ )
探究新知
高中数学
φ= ,ω=2
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
追问:此时 ,以(x , y)为坐标描点H ,点H 的轨迹对应的
y = sin(2x+ )
函数解析式是什么?
探究新知
高中数学
问题 s:函数y = sin(2x+ )与y = sin(x+ )的图象之间存
在怎样的变换关系?你能从质点的匀速圆周运动规律和 函数图象上点的坐标变化的角度进行解释吗?
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x+
探究新知
高中数学
)
从匀速圆周运动的变化规律看 , 两个动点都以Q1 为起
点 , 以 ω= 1和ω=2的不同角速度绕单位圆逆时针方向运动, 到达同一位置点P .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x+
探究新知
高中数学
)
当 ω= 1时到达点P 的时间为x s,因为ω=2时动点的转速
是 ω= 1时的2倍 ,所以 , 当 ω=2时到达点P的时间为 x s .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x+
探究新知
高中数学
)
对应地,设G(x , y)是函数y = sin(x+ )图象上的一点,
那么K( x, y)就是函数y = sin(2x + )图象上的相应点 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x
探究新知
高中数学
+ )
问题 ‘:我们找到了两个函数图象上任意点的变化,那么如何
从函数y = sin(x+ )的图象得到函数y = sin(2x + )的图象?
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x
探究新知
高中数学
+ )
总结:函数y = sin(2x + )的图象是把函数y = sin(x + )的图象
上所有点的横坐标缩短到原来的 (纵坐标不变)得到的 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
y = sin(2x+ )
y = sin(x
探究新知
高中数学
+ )
总结:函数y = sin(2x + )的图象是把函数y = sin(x + )的图象
上所有点的横坐标缩短到原来的 (纵坐标不变)得到的 . 并且 , y = sin(2x + )的周期为π , 是y = sin(x+ )的周期的 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
问题 7:如果ω取 ,3, 时,对应的函数y = sin( ωx+ )的图
象与y= sin(x+ )的图象之间存在怎样的变换关系?
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
分析: 当 ω= 时 ,动点的转速是ω=1时的 , 以Q1 为起点 ,到
达点P 的时间是ω=1时的2倍 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
E(2x, y)
y = sin( x+ )
6
π
2
1
G(x, y)
y = sin(x+ )
6
π
探究新知
高中数学
分析 :所以把y= sin(x+ )图象上所有点的横坐标伸长到原来
的2倍(纵坐标不变),就得到y= sin( x+ )的图象 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
E(2x, y)
y = sin( x+ )
6
π
2
1
G(x, y)
y = sin(x+ )
6
π
探究新知
高中数学
分析 :所以把y= sin(x+ )图象上所有点的横坐标伸长到原来
的2倍(纵坐标不变),就得到y= sin( x+ )的图象 .
并且,y = sin( x+ )的周期是4π , 是y = sin(x+ )的周期的2倍 .
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
总结:一般地,函数y = sin( ωx+φ)的周期是 , 把y = sin(x+φ)
图象上所有点的横坐标缩短(当ω>1时)或伸长(当0< ω<1时) 到原来的 倍(纵坐标不变),就得到 y = sin( ωx+φ)的图象 .
问题 8:结合上面的研究过程 ,你能给出ω( ω>0)的变化对函
数y = sin( ωx+φ)图象影响的一般化结论吗?
1.探索参数ω( ω>0)对函数y = sin( ωx+φ)图象的影响 .
探究新知
高中数学
问题 9:( 1)结合筒车模型 , A取不同值表示什么含义?
分析: A代表质点做匀速圆周运动的运动半径 , A取不同值表
示质点以不同的运动半径做匀速圆周运动 .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
高中数学
问题 9:(2)若给 A赋特殊值,你认为给 ,ω取哪个特殊值比
较合适?
分析:为了研究方便,不妨设 = , ω=2 ,固定 , ω的值 ,改
变参数A(A>0),研究函数y = Asin(2x+ )与y = sin(2x+ )的图象 之间的变换关系 .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
高中数学
问题 10: 函数y = 2sin(2x+ )与y = sin(2x+ )的图象之间
存在怎样的变换关系?你能从质点的匀速圆周运动规律和函 数图象上点的坐标变化的角度进行解释吗?
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
y = 2sin(2x+ )
y = sin(2x+ )
高中数学
分析:在以O1 为圆心,半径分别为 1 和 2 的圆上,两个动点分
别以Q1 和T1 为起点 , ω=2的转速经过x s后分别到达圆周上的点 P 和点T ,易得点T 的纵坐标是点P 的纵坐标的 2 倍 .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
y = 2sin(2x+ )
y = sin(2x+ )
高中数学
2y
y
分析:对应地,设K(x , y)是函数y = sin(2x+ )图象上的一点,
那么N(x , 2y)就是函数y = 2sin(2x + )图象上的相应点 .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
y = 2sin(2x+ )
y = sin(2x+ )
高中数学
2y
y
问题 11:我们找到了两个函数图象上任意点的变化 ,那么如何
从函数y = sin(2x+ )的图象得到函数y = 2sin(2x + )的图象?
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
y = 2sin(2x+ )
y = sin(2x+ )
高中数学
2y
y
总结: 函数y = 2sin(2x + )的图象是把函数y = sin(2x+ )的图
象上所有点的纵坐标伸长到原来的2倍(横坐标不变)得到的 .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
y = 2sin(2x+ )
y = sin(2x+ )
高中数学
2y
y
问题 12:如果A取 ,3 , 时,对应的函数y = Asin(2x+ )
的 图 象 与 y= sin(2x+ )的 图 象 之 间 存 在 怎 样 的 变 换 关 系? 你能给出 A(A>0)的变化对函数y = Asin( ωx+φ)图象 影响的一般化结论吗?
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
高中数学
总结: 函数y = Asin( ωx+φ)的图象 , 可以看作是把函数
y = sin( ωx+φ)的图象上所有点的纵坐标伸长(当 A>1时) 或缩短(当0<A<1时)为原来的 A倍(横坐标不变)而得 到.从而 ,函数y = Asin( ωx+φ)的值域是[-A, A],最大值 是A ,最小值是-A .
2 . 探索参数A(A>0)对函数y = Asin( ωx+φ)图象的影响 .
探究新知
高中数学
问题 13:我们分别研究了三个参数对函数y = Asin( ωx+φ)图
象的影响.并按照路线y = sin x y = sin(x+ ) y = sin(2x+ ) y = 2sin(2x+ ),你能总结一下这个变换过程吗?
3 .总结从正弦曲线出发 ,通过图象变换得到y= Asin( ωx+φ)的图象 .
探究新知
高中数学
y = sin(2x+ 伸长到原来的2 = 2sin(2x+ )
高中数学
6
π
y
倍
变
坐
不
纵
6 (横坐标
π)所有点的
π 所有点的横坐标缩短到原来的 1
y = sin(x+ ) 2
6 (纵坐标不变).
3 .总结从正弦曲线出发 ,通过图象变换得到y= Asin( ωx+φ)的图象 .
所有点向左平移 π 个单位长度 . y = sin x 6
y = sin(x+ )
y = sin(2x+ )
探究新知
追问: 你能总结一下从正弦函数y = sin x图象出发 ,通过图
象变换得到函数y = Asin( ωx+φ)(A>0,ω>0)图象的过程与 方法吗?
请填写在教科书第 236 页的表格中 .
3 .总结从正弦曲线出发 ,通过图象变换得到y= Asin( ωx+φ)的图象 .
探究新知
高中数学
y = sin(x+ = sin( x+Q)
y = sin( x+ )= Asin( x+Q)
高中数学
变
y
短
不
缩
(横坐标
>1时) 或
倍
A
) 为原来的A
坐标伸长(当
时
纵
(当0
Q)所
>
变)
y
长
不
伸
(纵坐标
1时)或
的
(
来
短
时)到原
横坐标缩
(
Q
3 .总结从正弦曲线出发 ,通过图象变换得到y= Asin( ωx+φ)的图象 .
所有点向左(当φ>0时)或向右(当φ<0时)
y = sin(x+Q)
平移 φ 个单位长度 .
探究新知
y = sin x
学以致用
练习: 已知函数y = 3sin x的图象为C .
(1) 为了得到函数y = 3sin 2x的图象 ,只要把C 上所有的点
(A)横坐标伸长到原来的2倍 ,纵坐标不变
(B)横坐标缩短到原来的 ,纵坐标不变
(C)纵坐标伸长到原来的2倍 ,横坐标不变
(D)纵坐标缩短到原来的 ,横坐标不变
高中数学
学以致用
练习: 已知函数y = 3sin x的图象为C .
(2) 为了得到函数y= 4sin x的图象 ,只要把C 上所有的点
(A)横坐标伸长到原来的 倍 ,纵坐标不变
(B)横坐标缩短到原来的 ,纵坐标不变
(C)纵坐标伸长到原来的 倍 ,横坐标不变
(D)纵坐标缩短到原来的 ,横坐标不变
高中数学
参数A , , 对
— 函数y = Asin( ωx +φ)
图象的影响
函数
y = Asin( x + )
函数 y = Asin( x + )的性质
现实世界中的
匀速圆周运动
课堂小结
高中数学
重点研究了 ,A 对函数 y = Asin( x + )图象的影响;
进 一 步体会从特殊到 一般 、 数形结合的思想方法;
发展数学抽象 、 逻辑推理以及直观想象的学科素养 .
课堂小结
高中数学
参数A , , 对
— 函数y = Asin( ωx +φ)
图象的影响
函数 y = Asin( x + )
的简单应用
现实世界中的
匀速圆周运动
函
y = Asi
x + )
数
n (
函数 y = Asin( x + )的性质
课堂小结
高中数学
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
