人教A版(2019)高数必修第一册 5.6.2不同函数增长的差异 课件(共30张PPT)
文档属性
| 名称 | 人教A版(2019)高数必修第一册 5.6.2不同函数增长的差异 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 407.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 09:58:52 | ||
图片预览


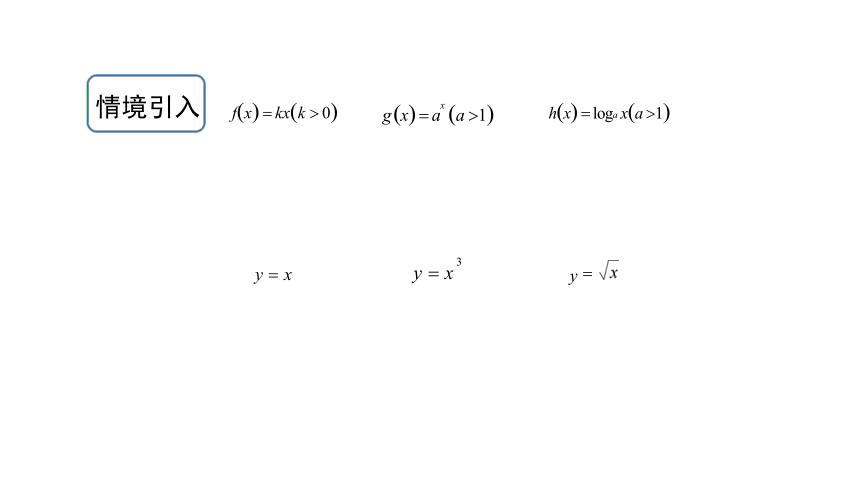






文档简介
(共30张PPT)
不同函数增长的差异
在我们学习过的 一 次函数 、 二 次函数 、 反比例函数 、 幂
函数 、 指数函数 、 对数函数中哪些函数在定义域上是增函数?
情境引入
高中数学
情境引入
h(x) = loga x(a >1)
g (x) = ax (a >1)
f(x) = kx(k > 0)
高中数学
3
y = x
y =
y = x
虽然它们都是增函数,但增长方式存在很大差异, 这种差异
正是不同类型现实问题具有不同增长规律的反映.
下面就来研究 一 次函数 f (x ) = kx + b, k > 0 , 指数函数g(x ) = ax (a > 1),
对数函数 h(x) = loga x(a >1) 在定义域内增长方式的差异.
我们采用由特殊到 一般, 由具体到抽象的研究方法.
情境引入
高中数学
分析: (1) 在区间(-∞ ,0)上, 指数函数 y=2x值恒大于0, 一 次函数 y=2x
值恒小于0, 所以我们重点研究在区间(0,+∞)上它们的增长差异.
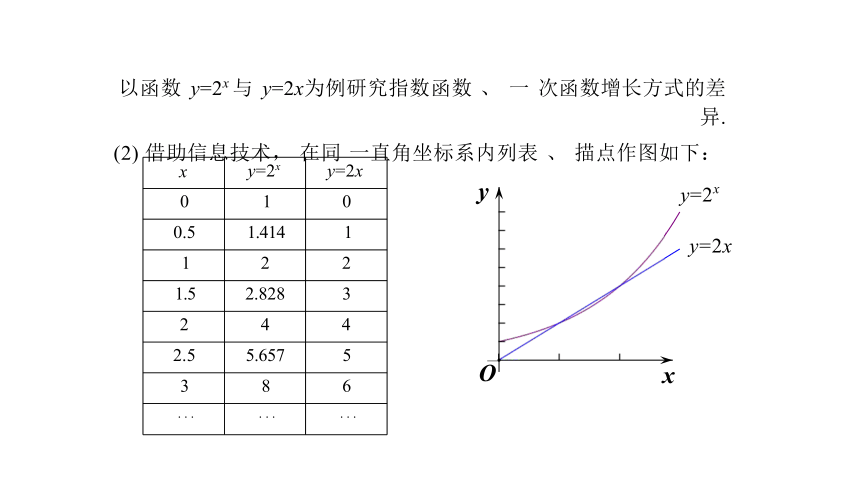
以函数 y=2x 与 y=2x为例研究指数函数 、 一 次函数增长方式的差异.
探究一:
高中数学
x y=2x
y=2x
0 1
0
0.5 1.414
1
1 2
2
1.5 2.828
3
2 4
4
2.5 5.657
5
3 8
6
· · · · · ·
· · ·
以函数 y=2x 与 y=2x为例研究指数函数 、 一 次函数增长方式的差异.
(2) 借助信息技术, 在同 一直角坐标系内列表 、 描点作图如下:
y=2x
y=2x
y
O
高中数学
x
综上: 虽然函数y=2x 与y=2x都是增函数, 但是它们的增长速度不
同, 函数y=2x的增长速度不变, 但是y=2x 的增长速度改变, 先慢 后快.
高中数学
(3) 观察两个函数图象及其增长方式:
结论 一: 函数y=2x 与y=2x有两个交点(1,2)和(2,4);
结论二: 在区间(0, 1)上, 函数y=2x 的图象位于y=2x之上;
结论三: 在区间(1,2)上, 函数y=2x 的图象位于y=2x之下; 结论四: 在区间(2,3)上, 函数y=2x 的图象位于y=2x之上.
y
8
7
6
5
4
3
2
1
O
1 2 x
(1,2)
(2,4)
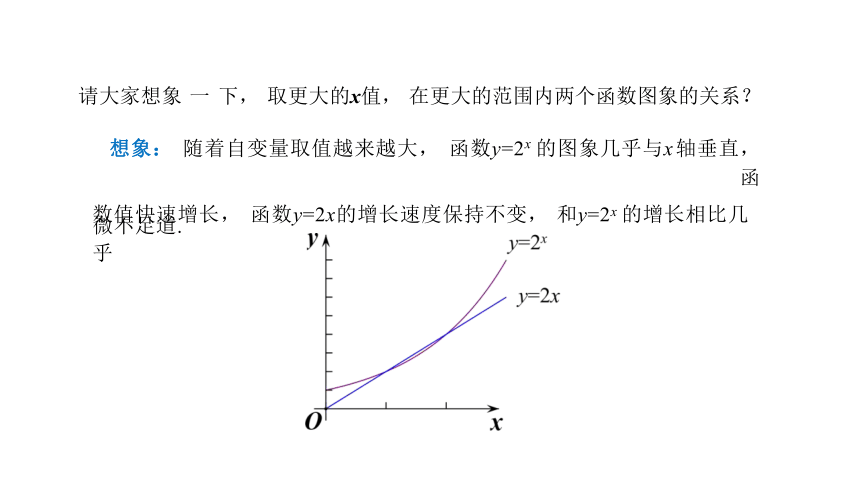
请大家想象 一 下, 取更大的x值, 在更大的范围内两个函数图象的关系?
想象: 随着自变量取值越来越大, 函数y=2x 的图象几乎与x 轴垂直, 函
数值快速增长, 函数y=2x的增长速度保持不变, 和y=2x 的增长相比几乎
微不足道.
高中数学
总结 一: 函数 y=2x与 y=2x在[0,+∞)上增长快慢的不同如下:
虽然函数 y=2x与 y=2x在[0,+∞)上都是单调递增, 但它们的增长速度
不同, 而且不在 一 个“档次 ”.
随着x 的增大,y=2x 的增长速度越来越快, 会超过并远远大于y=2x的
增长速度.
尽管在x 的 一 定范围内, 2x<2x, 但由于y=2x 的增长最终会快于y=2x
的增长, 因此, 总会存在 一 个x0, 当x>x0 时, 恒有2x>2x.
高中数学
总结二: 一般地指数函数 y=ax(a>1)与 一 次函数 y=kx(k>0)的增长都
与上述类似.
即使k值远远大于a值, 指数函数 y=ax(a>1)虽然有 一段区间会小于
y=kx(k>0), 但总会存在 一 个x0, 当x>x0 时,y=ax(a>1)的增长速度会大 大超过 y=kx(k>0)的增长速度.
高中数学
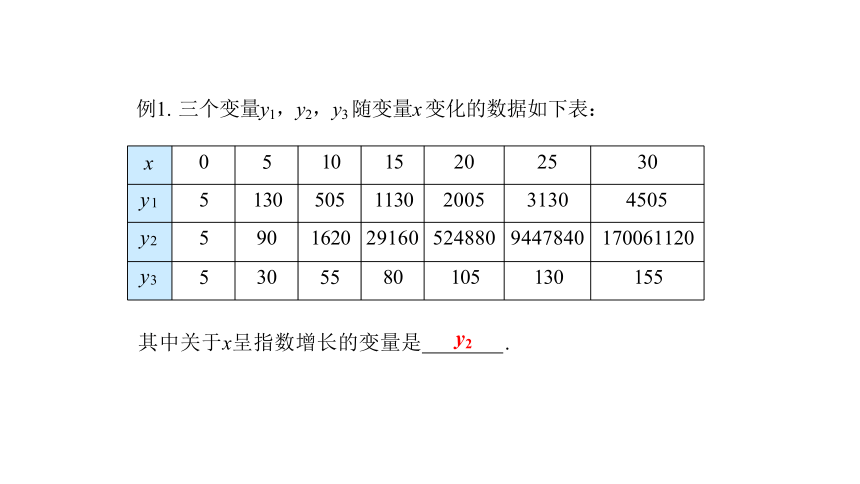
x 0 5 10 15 20 25
30
y1 5 130 505 1130 2005 3130
4505
y2 5 90 1620 29160 524880 9447840
170061120
y3 5 30 55 80 105 130
155
例1. 三个变量y1,y2,y3 随变量x 变化的数据如下表:
其中关于x呈指数增长的变量是 y2 .
高中数学
分析: (1) 在区间(-∞ ,0)上, 对数函数 y=lgx没意义, 一 次函数值恒小于
0, 所以研究在区间(0,+∞)上它们的增长差异.
x 为例研究对数函数 、 一 次函数增长方式的差异.
探究二:以函数 y=lgx与y =
高中数学
10
1
x y=lgx
1
y = 10 x
0 不存在
0
10 1
1
20 1.301
2
30 1.477
3
40 1.602
4
50 1.699
5
60 1.778
6
· · · · · ·
· · ·
以函数 y=lgx与y = x 为例研究对数函数 、 一 次函数增长方式的差异.
(2) 借助信息技术, 在同 一直角坐标系内列表 、 描点作图如下:
y = x
y=lgx
y
6
5
4
3
2
1
O
10 20 30 40 50 60 x
高中数学
(3) 观察两个函数图象及其增长方式:
总结 一: 虽然函数 y=lgx与 y = x 在(0,+∞)上都是单调递增, 但它们的
增长速度存在明显差异.
在(0,+∞)上增长速度不变, y=lgx在(0,+∞)上的增长速度在变化.
, 而函数y=lgx的图象越来
越平缓, 就像与x轴平行 一样.
的图象离x轴越来越远
y
6
5
4
3
2
1
O
随着x 的增大,
10 20 30 40 50 60 x
1 y = 10 x
高中数学
1
x
10
1
x
10
y=lgx
y =
y =
例如: lg10= 1, lg100=2, lg1000=3, lg10000=4;
10 = 1, 100 = 10, 1000 = 100, 10000 = 1000.
这表明, 当x>10, 即y>1,y=lgx 比 y = x 相比增长得就很慢了.
y
6
5
4
3
2
1
O
10 20 30 40 50 60 x
1 y = 10 x
y=lgx
高中数学
思考: 将y=lgx放大1000倍, 将函数y= 1000lgx与 y =
律吗? 先想象 一 下, 仍然有.
y
14770
12660
10550
8440
6330
4220
2110
O
2110 4220 6330 8440 10550 12660 14770 16880 18990 21100 23210 25320 27430 29540 31650 33760 35870 37980 40090 42200 44310 46420 48530 50640 52750
比较, 仍有上面规
高中数学
1
x
10
x
总结二: 一般地, 虽然对数函数y = loga x(a >1) 与 一 次函数 y=kx(k>0)在
(0,+∞)上都是单调递增, 但它们的增长速度不同.
随着x 的增大, 一 次函数 y=kx(k>0)保持固定的增长速度, 而对数 函数 y = loga x(a >1) 的增长速度越来越慢.
不论a值比k值大多少, 在 一 定范围内,loga x (a >1)可能会大于kx, 但 由于loga x (a >1)的增长会慢于kx 的增长, 因此总存在 一 个x0, 当x>x0 时, 恒有 log a x < kx .
高中数学
例2. 函数的图象如图所示 .
( 1 ) 试根据函数的增长差异指出
曲线C1, C2 分别对应的函数;
(2 ) 比较两函数的增长差异(以两
图象交点为分界点, 对 f (x ) , g (x) 的大小进行比较).
高中数学
例2. 函数的图象如图所示 .
( 1 ) 试根据函数的增长差异指出
曲线C1, C2 分别对应的函数;
(2 ) 比较两函数的增长差异(以两
图象交点为分界点, 对 f (x ) , g (x) 的大小进行比较).
解:( 1 ) C1 对应的函数为g(x)=0.3x- 1, C2 对应的函数为f(x)=lg x.
(2 ) 当xf(x); 当x1g(x);
当x>x2 时, g(x)>f(x); 当x =x1 或x =x2 时,f(x)=g(x) .
高中数学
探究三:
(1)画出 一 次函数 y = 2x , 对数函数y = lg x 和指数函数y = 2x 的图象,
并比较它们的增长差异.
高中数学
总结 一: 虽然函数 y = 2x, 函数 y = lg x与 y = 2x在(0,+∞)上都是单调递
增, 但它们的增长速度存在明显差异.
y = 2x 在(0,+∞)上增长速度不变, 函数 y = lg x与 y = 2x 在(0,+∞)上
的增长速度在变化.
函数 y = 2x 的图象越来越陡, 就像与 x轴垂直 一样; 函数 y = lg x
的图象越来越平缓, 就像与 轴平行 一样.
高中数学
(2)概括 一 次函数 y = kx (k > 0) , 对数函数y = loga x (a >1)和指数函数 y = bx (b >1) 的增长差异.
高中数学
总结二: 一般地, 虽然 一 次函数y = kx (k > 0), 对数函数 y = loga x (a >1)和指数函数
y = bx (b >1)在(0,+∞)上都是单调递增, 但它们的增长速度不同.
随着x 的增大, 一 次函数 y = kx (k > 0保持固定的增长速度, 而指数函数 y = bx (b>1的增长速度越来越快; 对数函数 y = loga x (a > 的增长速度越来越慢.
不论b值比k值小多少, 在 一 定范围内,bx 可能会小于kx, 但由于bx 的增长会快 于kx 的增长, 因此总存在 一 个x0, 当 x > x0 时, 恒有bx > kx;
同样, 不论a 值比k值大多少, 在 一 定范围内,loga x (a > 1)可能会大于kx, 但由
于loga x (a >1) 的增长会慢于kx的增长, 因此总存在 一 个x0 , 当 x > x0 时, 恒有 loga x < .kx .
高中数学
总结二: 一般地, 虽然 一 次函数y = kx (k > 0), 对数函数 y = loga x (a >1)
和指数函数 y = bx (b >1) 在(0,+∞)上都是单调递增, 但它们的增长速度 不同.
随着x 的增大, 一 次函数 y = kx (k > 0保持固定的增长速度, 而指 数函数 y = bx (b >1的增长速度越来越快; 对数函数 y = loga x (a > 的 增长速度越来越慢.
高中数学
(3 ) 讨论交流“ 直线上升 ”“ 对数增长 ”“指数爆炸 ” 的含义 .
高中数学
直线上升: 增长速度不变, 是 一 个固定的值;
对数增长: 增长速度越来越慢, 图象越来越平缓, 就像与x 轴平行 一样;
指数爆炸: 增长速度越来越快, 以相同倍数增加, 图象越来越陡, 最终就
像与 x轴垂直 一样.
(3 ) 讨论交流“ 直线上升 ”“ 对数增长 ”“指数爆炸 ” 的含义 .
高中数学
例3. 下列函数中随x 的增大而增大且速度最快的是( ) .
A. y = ex B. y = ln x
C. y = x2 D. y = e-x
高中数学
例3. 下列函数中随x 的增大而增大且速度最快的是( ) .
A. y = ex B. y = ln x
C. y = x2 D. y = e-x
高中数学
由特殊到 一般, 由具体到抽象研究了 一 次函数f(x)=kx+b ,k>0, 指数 函数 g(x)=ax(a>1) , 对数函数 h(x) = loga x(a >1) 在定义域上的不同增长方式.
以后会经常用到“ 直线上升 ” 、 “指数爆炸 ” 、 “ 对数增长 ”.
把握了不同函数增长方式的差异, 就可以根据现实问题的增长情况, 选择
合适的函数模型刻画现实问题的变化规律, 学以致用.
课堂小结
高中数学
通过这节课, 同学们有什么感悟呢?
希望每位同学遇到困难都不要轻言放弃, 如同 指数函数 一般, 即使 一 开始进步缓慢, 但这正是积 淀的过程, 不断的积累, 最终 一 定会走向卓越, 成 就自己
高中数学
不同函数增长的差异
在我们学习过的 一 次函数 、 二 次函数 、 反比例函数 、 幂
函数 、 指数函数 、 对数函数中哪些函数在定义域上是增函数?
情境引入
高中数学
情境引入
h(x) = loga x(a >1)
g (x) = ax (a >1)
f(x) = kx(k > 0)
高中数学
3
y = x
y =
y = x
虽然它们都是增函数,但增长方式存在很大差异, 这种差异
正是不同类型现实问题具有不同增长规律的反映.
下面就来研究 一 次函数 f (x ) = kx + b, k > 0 , 指数函数g(x ) = ax (a > 1),
对数函数 h(x) = loga x(a >1) 在定义域内增长方式的差异.
我们采用由特殊到 一般, 由具体到抽象的研究方法.
情境引入
高中数学
分析: (1) 在区间(-∞ ,0)上, 指数函数 y=2x值恒大于0, 一 次函数 y=2x
值恒小于0, 所以我们重点研究在区间(0,+∞)上它们的增长差异.
以函数 y=2x 与 y=2x为例研究指数函数 、 一 次函数增长方式的差异.
探究一:
高中数学
x y=2x
y=2x
0 1
0
0.5 1.414
1
1 2
2
1.5 2.828
3
2 4
4
2.5 5.657
5
3 8
6
· · · · · ·
· · ·
以函数 y=2x 与 y=2x为例研究指数函数 、 一 次函数增长方式的差异.
(2) 借助信息技术, 在同 一直角坐标系内列表 、 描点作图如下:
y=2x
y=2x
y
O
高中数学
x
综上: 虽然函数y=2x 与y=2x都是增函数, 但是它们的增长速度不
同, 函数y=2x的增长速度不变, 但是y=2x 的增长速度改变, 先慢 后快.
高中数学
(3) 观察两个函数图象及其增长方式:
结论 一: 函数y=2x 与y=2x有两个交点(1,2)和(2,4);
结论二: 在区间(0, 1)上, 函数y=2x 的图象位于y=2x之上;
结论三: 在区间(1,2)上, 函数y=2x 的图象位于y=2x之下; 结论四: 在区间(2,3)上, 函数y=2x 的图象位于y=2x之上.
y
8
7
6
5
4
3
2
1
O
1 2 x
(1,2)
(2,4)
请大家想象 一 下, 取更大的x值, 在更大的范围内两个函数图象的关系?
想象: 随着自变量取值越来越大, 函数y=2x 的图象几乎与x 轴垂直, 函
数值快速增长, 函数y=2x的增长速度保持不变, 和y=2x 的增长相比几乎
微不足道.
高中数学
总结 一: 函数 y=2x与 y=2x在[0,+∞)上增长快慢的不同如下:
虽然函数 y=2x与 y=2x在[0,+∞)上都是单调递增, 但它们的增长速度
不同, 而且不在 一 个“档次 ”.
随着x 的增大,y=2x 的增长速度越来越快, 会超过并远远大于y=2x的
增长速度.
尽管在x 的 一 定范围内, 2x<2x, 但由于y=2x 的增长最终会快于y=2x
的增长, 因此, 总会存在 一 个x0, 当x>x0 时, 恒有2x>2x.
高中数学
总结二: 一般地指数函数 y=ax(a>1)与 一 次函数 y=kx(k>0)的增长都
与上述类似.
即使k值远远大于a值, 指数函数 y=ax(a>1)虽然有 一段区间会小于
y=kx(k>0), 但总会存在 一 个x0, 当x>x0 时,y=ax(a>1)的增长速度会大 大超过 y=kx(k>0)的增长速度.
高中数学
x 0 5 10 15 20 25
30
y1 5 130 505 1130 2005 3130
4505
y2 5 90 1620 29160 524880 9447840
170061120
y3 5 30 55 80 105 130
155
例1. 三个变量y1,y2,y3 随变量x 变化的数据如下表:
其中关于x呈指数增长的变量是 y2 .
高中数学
分析: (1) 在区间(-∞ ,0)上, 对数函数 y=lgx没意义, 一 次函数值恒小于
0, 所以研究在区间(0,+∞)上它们的增长差异.
x 为例研究对数函数 、 一 次函数增长方式的差异.
探究二:以函数 y=lgx与y =
高中数学
10
1
x y=lgx
1
y = 10 x
0 不存在
0
10 1
1
20 1.301
2
30 1.477
3
40 1.602
4
50 1.699
5
60 1.778
6
· · · · · ·
· · ·
以函数 y=lgx与y = x 为例研究对数函数 、 一 次函数增长方式的差异.
(2) 借助信息技术, 在同 一直角坐标系内列表 、 描点作图如下:
y = x
y=lgx
y
6
5
4
3
2
1
O
10 20 30 40 50 60 x
高中数学
(3) 观察两个函数图象及其增长方式:
总结 一: 虽然函数 y=lgx与 y = x 在(0,+∞)上都是单调递增, 但它们的
增长速度存在明显差异.
在(0,+∞)上增长速度不变, y=lgx在(0,+∞)上的增长速度在变化.
, 而函数y=lgx的图象越来
越平缓, 就像与x轴平行 一样.
的图象离x轴越来越远
y
6
5
4
3
2
1
O
随着x 的增大,
10 20 30 40 50 60 x
1 y = 10 x
高中数学
1
x
10
1
x
10
y=lgx
y =
y =
例如: lg10= 1, lg100=2, lg1000=3, lg10000=4;
10 = 1, 100 = 10, 1000 = 100, 10000 = 1000.
这表明, 当x>10, 即y>1,y=lgx 比 y = x 相比增长得就很慢了.
y
6
5
4
3
2
1
O
10 20 30 40 50 60 x
1 y = 10 x
y=lgx
高中数学
思考: 将y=lgx放大1000倍, 将函数y= 1000lgx与 y =
律吗? 先想象 一 下, 仍然有.
y
14770
12660
10550
8440
6330
4220
2110
O
2110 4220 6330 8440 10550 12660 14770 16880 18990 21100 23210 25320 27430 29540 31650 33760 35870 37980 40090 42200 44310 46420 48530 50640 52750
比较, 仍有上面规
高中数学
1
x
10
x
总结二: 一般地, 虽然对数函数y = loga x(a >1) 与 一 次函数 y=kx(k>0)在
(0,+∞)上都是单调递增, 但它们的增长速度不同.
随着x 的增大, 一 次函数 y=kx(k>0)保持固定的增长速度, 而对数 函数 y = loga x(a >1) 的增长速度越来越慢.
不论a值比k值大多少, 在 一 定范围内,loga x (a >1)可能会大于kx, 但 由于loga x (a >1)的增长会慢于kx 的增长, 因此总存在 一 个x0, 当x>x0 时, 恒有 log a x < kx .
高中数学
例2. 函数的图象如图所示 .
( 1 ) 试根据函数的增长差异指出
曲线C1, C2 分别对应的函数;
(2 ) 比较两函数的增长差异(以两
图象交点为分界点, 对 f (x ) , g (x) 的大小进行比较).
高中数学
例2. 函数的图象如图所示 .
( 1 ) 试根据函数的增长差异指出
曲线C1, C2 分别对应的函数;
(2 ) 比较两函数的增长差异(以两
图象交点为分界点, 对 f (x ) , g (x) 的大小进行比较).
解:( 1 ) C1 对应的函数为g(x)=0.3x- 1, C2 对应的函数为f(x)=lg x.
(2 ) 当x
当x>x2 时, g(x)>f(x); 当x =x1 或x =x2 时,f(x)=g(x) .
高中数学
探究三:
(1)画出 一 次函数 y = 2x , 对数函数y = lg x 和指数函数y = 2x 的图象,
并比较它们的增长差异.
高中数学
总结 一: 虽然函数 y = 2x, 函数 y = lg x与 y = 2x在(0,+∞)上都是单调递
增, 但它们的增长速度存在明显差异.
y = 2x 在(0,+∞)上增长速度不变, 函数 y = lg x与 y = 2x 在(0,+∞)上
的增长速度在变化.
函数 y = 2x 的图象越来越陡, 就像与 x轴垂直 一样; 函数 y = lg x
的图象越来越平缓, 就像与 轴平行 一样.
高中数学
(2)概括 一 次函数 y = kx (k > 0) , 对数函数y = loga x (a >1)和指数函数 y = bx (b >1) 的增长差异.
高中数学
总结二: 一般地, 虽然 一 次函数y = kx (k > 0), 对数函数 y = loga x (a >1)和指数函数
y = bx (b >1)在(0,+∞)上都是单调递增, 但它们的增长速度不同.
随着x 的增大, 一 次函数 y = kx (k > 0保持固定的增长速度, 而指数函数 y = bx (b>1的增长速度越来越快; 对数函数 y = loga x (a > 的增长速度越来越慢.
不论b值比k值小多少, 在 一 定范围内,bx 可能会小于kx, 但由于bx 的增长会快 于kx 的增长, 因此总存在 一 个x0, 当 x > x0 时, 恒有bx > kx;
同样, 不论a 值比k值大多少, 在 一 定范围内,loga x (a > 1)可能会大于kx, 但由
于loga x (a >1) 的增长会慢于kx的增长, 因此总存在 一 个x0 , 当 x > x0 时, 恒有 loga x < .kx .
高中数学
总结二: 一般地, 虽然 一 次函数y = kx (k > 0), 对数函数 y = loga x (a >1)
和指数函数 y = bx (b >1) 在(0,+∞)上都是单调递增, 但它们的增长速度 不同.
随着x 的增大, 一 次函数 y = kx (k > 0保持固定的增长速度, 而指 数函数 y = bx (b >1的增长速度越来越快; 对数函数 y = loga x (a > 的 增长速度越来越慢.
高中数学
(3 ) 讨论交流“ 直线上升 ”“ 对数增长 ”“指数爆炸 ” 的含义 .
高中数学
直线上升: 增长速度不变, 是 一 个固定的值;
对数增长: 增长速度越来越慢, 图象越来越平缓, 就像与x 轴平行 一样;
指数爆炸: 增长速度越来越快, 以相同倍数增加, 图象越来越陡, 最终就
像与 x轴垂直 一样.
(3 ) 讨论交流“ 直线上升 ”“ 对数增长 ”“指数爆炸 ” 的含义 .
高中数学
例3. 下列函数中随x 的增大而增大且速度最快的是( ) .
A. y = ex B. y = ln x
C. y = x2 D. y = e-x
高中数学
例3. 下列函数中随x 的增大而增大且速度最快的是( ) .
A. y = ex B. y = ln x
C. y = x2 D. y = e-x
高中数学
由特殊到 一般, 由具体到抽象研究了 一 次函数f(x)=kx+b ,k>0, 指数 函数 g(x)=ax(a>1) , 对数函数 h(x) = loga x(a >1) 在定义域上的不同增长方式.
以后会经常用到“ 直线上升 ” 、 “指数爆炸 ” 、 “ 对数增长 ”.
把握了不同函数增长方式的差异, 就可以根据现实问题的增长情况, 选择
合适的函数模型刻画现实问题的变化规律, 学以致用.
课堂小结
高中数学
通过这节课, 同学们有什么感悟呢?
希望每位同学遇到困难都不要轻言放弃, 如同 指数函数 一般, 即使 一 开始进步缓慢, 但这正是积 淀的过程, 不断的积累, 最终 一 定会走向卓越, 成 就自己
高中数学
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
