5.3.1平行线性质[1]
文档属性
| 名称 | 5.3.1平行线性质[1] |  | |
| 格式 | rar | ||
| 文件大小 | 166.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-10 21:21:00 | ||
图片预览




文档简介
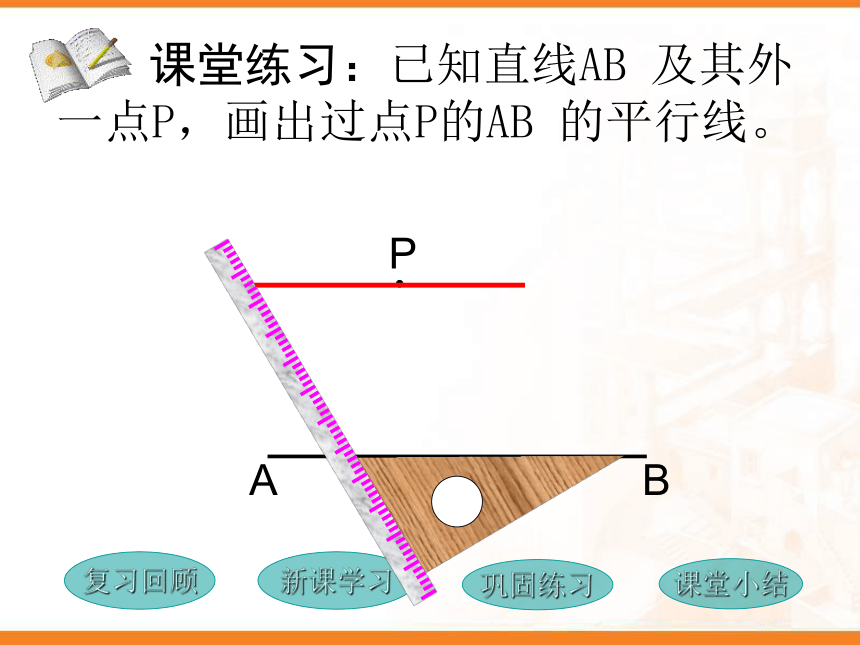
课件17张PPT。复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结 课堂练习:已知直线AB 及其外一点P,画出过点P的AB 的平行线。 平行线的判定方法有哪三种?它
们是先知道什么……、 后知道什么? 同位角相等
内错角相等
同旁内角互补两直线平行问题复习回顾新课学习巩固练习课堂小结如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。问题演示……结论性质2复习回顾新课学习巩固练习课堂小结演示结论
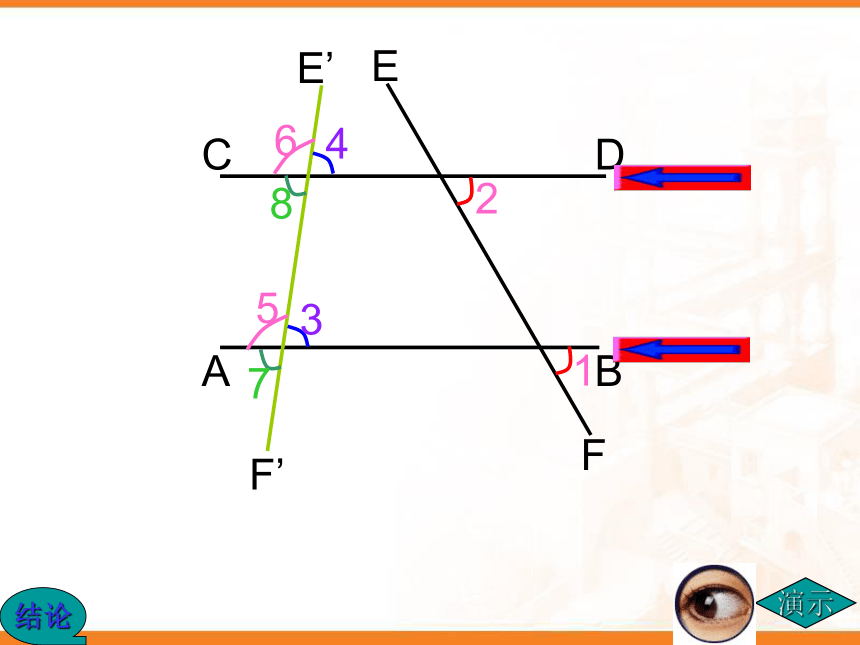
a//b (已知)
?1=?2 (两直线平行,同位角相等)
又 ?1=?3(对顶角相等)
?3=?2(等量代换)
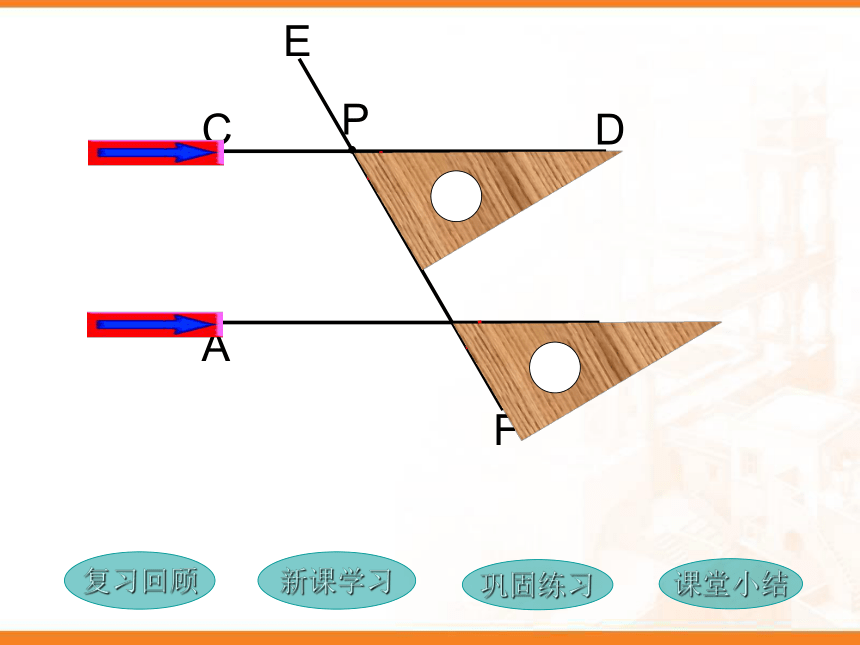
思考回答????如图,已知:a// b
那么?3与?2有什么关系? 平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。结论复习回顾性质3巩固练习课堂小结c
解: a//b (已知)
? 1= ? 2(两直线平行,同位角相等)
? 1+ ? 3=180°(邻补角定义)
? 2+ ? 3=180°(等量代换)
如图:已知a//b,那么?2与? 3有什么关系呢?平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
????复习回顾性质1巩固练习课堂小结平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
精彩回放复习回顾新课学习巩固练习课堂小结解:∵AD//BC (已知)
∴? A + ? B=180°
(两直线平行,同旁内角互补)
即 ? B= 180 °- ? A =180 ° -115 ° =65 °
∵AD//BC (已知)
∴? D+ ? C=180 °
(两直线平行,同旁内角互补)
即? C=180 °- ? D =180 ° -100 ° =80 °
答:梯形的另外两个角分别为65 ° 、80 ° 。复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结解答:∵AB∥CD(已知)∴∠B=∠C(两直线平行,内错角相等)又∵∠B=142°∴∠B=∠C=142°(已知)(等量代换)P.86EX.1(1)∵AB∥CD(已知)∴∠1=∠2(两直线平行,内错角相等)又∵∠1=110°∴∠1=∠2=110°(已知)(等量代换)(2)∵AB∥CD(已知)∴∠1=∠3(两直线平行,同位角相等)又∵∠1=110°∴∠1=∠3=110°(已知)(等量代换)(3)∵AB∥CD(已知)∴∠1+∠4=180°(两直线平行,内错角相等)又∵∠1=110°(已知)∴110 ° +∠4=180°(等量代换)∴∠4=180°-110°=70°(等式性质)解答:P.86EX.2 已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。复习回顾新课学习巩固练习课堂小结如图: ?1= ? 2(已知)
AD//
( )
? BCD+ ? D=180?
( )BC内错角相等,两直线平行两直线平行,同旁内角互补???填空:复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结(已知)(1)∵∠ADE=60 ° ∠B=60 °∴∠ADE=∠B(等量代换)又∵∠ADE =∠B (已证)∴DE∥BC(同位角相等,两直线平行)(2)∵ DE∥BC(已证)∴∠AED=∠C(两直线平行,同位角相等)又∵∠AED=40°(已知)(等量代换)∴∠C=40 °解答:P.86EX.3同位角相等
内错角相等
同旁内角互补两直线平行判定性质小结:复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结再见
们是先知道什么……、 后知道什么? 同位角相等
内错角相等
同旁内角互补两直线平行问题复习回顾新课学习巩固练习课堂小结如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。问题演示……结论性质2复习回顾新课学习巩固练习课堂小结演示结论
a//b (已知)
?1=?2 (两直线平行,同位角相等)
又 ?1=?3(对顶角相等)
?3=?2(等量代换)
思考回答????如图,已知:a// b
那么?3与?2有什么关系? 平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。结论复习回顾性质3巩固练习课堂小结c
解: a//b (已知)
? 1= ? 2(两直线平行,同位角相等)
? 1+ ? 3=180°(邻补角定义)
? 2+ ? 3=180°(等量代换)
如图:已知a//b,那么?2与? 3有什么关系呢?平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
????复习回顾性质1巩固练习课堂小结平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
精彩回放复习回顾新课学习巩固练习课堂小结解:∵AD//BC (已知)
∴? A + ? B=180°
(两直线平行,同旁内角互补)
即 ? B= 180 °- ? A =180 ° -115 ° =65 °
∵AD//BC (已知)
∴? D+ ? C=180 °
(两直线平行,同旁内角互补)
即? C=180 °- ? D =180 ° -100 ° =80 °
答:梯形的另外两个角分别为65 ° 、80 ° 。复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结解答:∵AB∥CD(已知)∴∠B=∠C(两直线平行,内错角相等)又∵∠B=142°∴∠B=∠C=142°(已知)(等量代换)P.86EX.1(1)∵AB∥CD(已知)∴∠1=∠2(两直线平行,内错角相等)又∵∠1=110°∴∠1=∠2=110°(已知)(等量代换)(2)∵AB∥CD(已知)∴∠1=∠3(两直线平行,同位角相等)又∵∠1=110°∴∠1=∠3=110°(已知)(等量代换)(3)∵AB∥CD(已知)∴∠1+∠4=180°(两直线平行,内错角相等)又∵∠1=110°(已知)∴110 ° +∠4=180°(等量代换)∴∠4=180°-110°=70°(等式性质)解答:P.86EX.2 已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。复习回顾新课学习巩固练习课堂小结如图: ?1= ? 2(已知)
AD//
( )
? BCD+ ? D=180?
( )BC内错角相等,两直线平行两直线平行,同旁内角互补???填空:复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结(已知)(1)∵∠ADE=60 ° ∠B=60 °∴∠ADE=∠B(等量代换)又∵∠ADE =∠B (已证)∴DE∥BC(同位角相等,两直线平行)(2)∵ DE∥BC(已证)∴∠AED=∠C(两直线平行,同位角相等)又∵∠AED=40°(已知)(等量代换)∴∠C=40 °解答:P.86EX.3同位角相等
内错角相等
同旁内角互补两直线平行判定性质小结:复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结再见
