平行四边形性质和判定(安徽省)(无答案)
文档属性
| 名称 | 平行四边形性质和判定(安徽省)(无答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 110.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-04 00:00:00 | ||
图片预览

文档简介
《平行四边形的性质和判定》单元测试080421
姓名__________
一.填空(4×12分)
1.在□ABCD中,∠A+∠C=200o,则∠A=__________;∠B=__________.
2.在四边形ABCD中,已知AD∥BC,要使四边形ABCD是平行四边形,需要增加条件___________(只需填一个你认为正确的条件).
3.在□ABCD中,∠CBD=70o,BC=BD,则∠ADC=__________.
4.□ABCD的周长为120cm,对角线AC和BD相交于点O,且△AOB的周长比△BOC周长大16cm,则AB=___________,BC=____________.
5.如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60o,则∠B=_______;若BC=4cm,AB=3cm,则AF=___________,□ABCD的面积为_________.
6.如图,□ABCD中,AB⊥AC, E为边AD上的点,G为AB的中点,GF∥AC交BC于点F.若□ABCD的面积16cm2,AB=4cm,则△EBC的面积为__________,△CFG的面积为__________,△AGF的面积为_____________,GF= ______cm.
(第5题图) (第6题图) (第7题图)
7.如图,在□ABCD中,DE是∠ADC的平分线,F是AB的中点,AB=4,BC=6,则BE∶EF∶FC=__________.
8.□ABCD中,对角线AC,BD交于点O,若AB=6,AC=10,则BD的长的取值范围为____________________.
9.已知任意直线把.□ABCD分成两部分,要使这两部分的面积相等,直线所在的位置需满足的条件是
________________________________________________________
10.如图 在中,,点,,分别在,,上,四边形为平行四边形,,□ABCD的周长是_____________
11.已知点在面积为4的平行四边形的边上运动,使的面积为1的点共有 个.
12.在平面直角坐标系中,点的坐标分别为.若四边形为平行四边形,那么点的坐标是 .
二。选择题(3×8)
13.下列图案中,不是中心对称图形的是( )
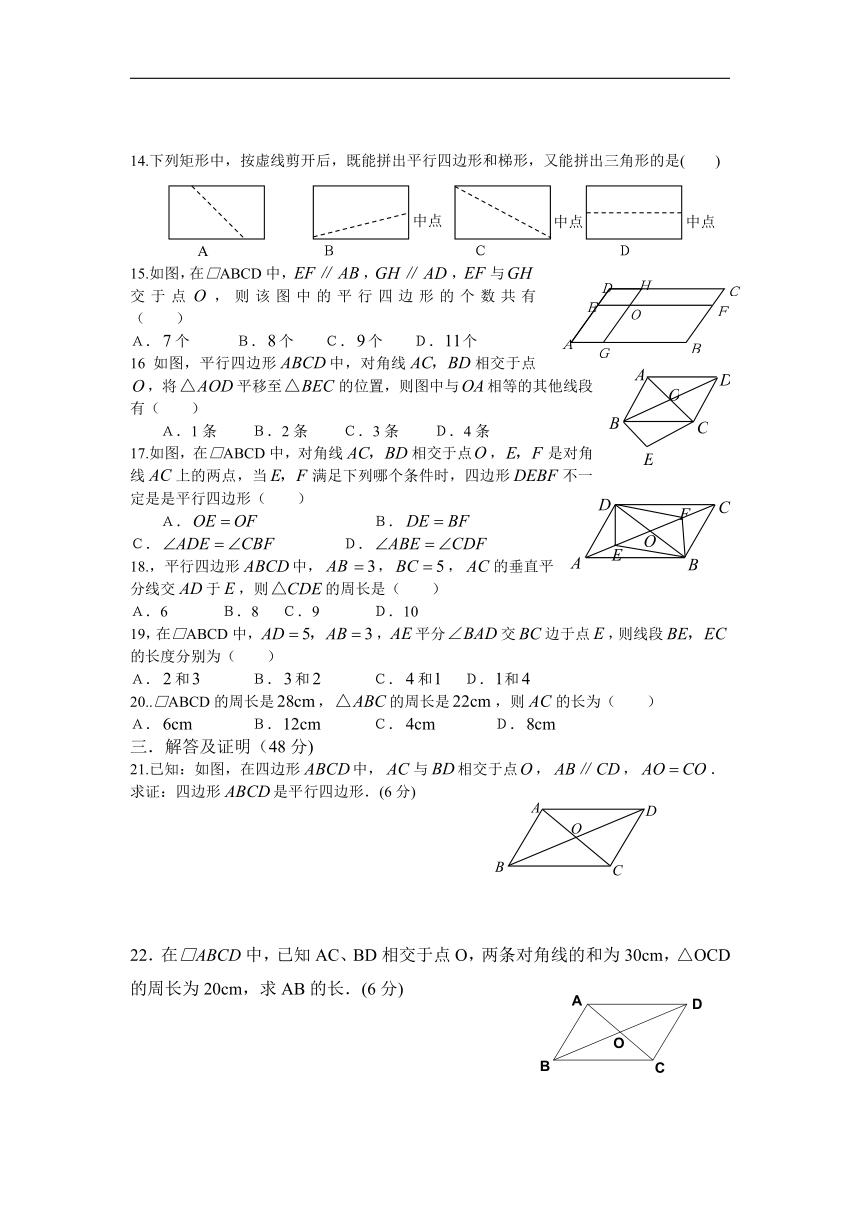
14.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是( )
A B C D
15.如图,在□ABCD中,,,与交于点,则该图中的平行四边形的个数共有 ( )
A.个 B.个 C.个 D.个
16 如图,平行四边形中,对角线相交于点,将平移至的位置,则图中与相等的其他线段有( )
A.1条 B.2条 C.3条 D.4条
17.如图,在□ABCD中,对角线相交于点,是对角线上的两点,当满足下列哪个条件时,四边形不一定是是平行四边形( )
A. B.
C. D.
18.,平行四边形中,,,的垂直平分线交于,则的周长是( )
A.6 B.8 C.9 D.10
19,在□ABCD中,,平分交边于点,则线段的长度分别为( )
A.和 B.和 C.和 D.和
20..□ABCD的周长是,的周长是,则的长为( )
A. B. C. D.
三.解答及证明(48分)
21.已知:如图,在四边形中,与相交于点,,.
求证:四边形是平行四边形.(6分)
22.在□ABCD中,已知AC、BD相交于点O,两条对角线的和为30cm,△OCD的周长为20cm,求AB的长.(6分)
23.如图,四边形ABCD中,AD∥BC,OE=OF,OA=OC,问四边形ABCD是平行四边形吗?为什么?(8分)
24.已知:如图,AC是平行四边形ABCD的对角线,MN∥AC,分别交DA、DC于M、N,交AB、BC的延长线于点P、Q.求证:MQ=PN.(8分)
25.在等腰△ABC中,AB=AC,点D是直线BC上一点,DE∥AC交直线AB于E,DF∥AB交直线AC于点F,解答下列各问:
(1)如图1,当点D在线段BC上时,有DE+DF=AB,请你说明理由;(6分)
(2)如图2,当点D在线段BC的延长线上时,请你参考(1)画出正确的图形,并写出线段DE、DF、AB之间的关系.(4分)
(图1) (图2)
26.(10分) 已知任意四边形,且线段、、、、、的中点分别是、、、、、.
(1)若四边形如图①,判断下列结论是否正确(正确的在括号里填“√”,错误的在括号里填“×”).
甲:顺次连接、、、一定得到平行四边形;( )
乙:顺次连接、、、一定得到平行四边形.( )
(2)请选择甲、乙中的一个,证明你对它的判断.
(3)若四边形如图②,请你判断(1)中的两个结论是否成立?
附加题. 如图,已知四边形纸片,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片.如果限定裁剪线最多有两条,能否做到: (用“能”或“不能”填空).若填“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.
A
B
C
D
中点
中点
中点
D
H
C
F
O
E
A
G
B
A
B
C
D
O
图②
A
D
C
B
F
B
E
A
D
C
H
P
图①
G
Q
A
B
C
D
姓名__________
一.填空(4×12分)
1.在□ABCD中,∠A+∠C=200o,则∠A=__________;∠B=__________.
2.在四边形ABCD中,已知AD∥BC,要使四边形ABCD是平行四边形,需要增加条件___________(只需填一个你认为正确的条件).
3.在□ABCD中,∠CBD=70o,BC=BD,则∠ADC=__________.
4.□ABCD的周长为120cm,对角线AC和BD相交于点O,且△AOB的周长比△BOC周长大16cm,则AB=___________,BC=____________.
5.如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60o,则∠B=_______;若BC=4cm,AB=3cm,则AF=___________,□ABCD的面积为_________.
6.如图,□ABCD中,AB⊥AC, E为边AD上的点,G为AB的中点,GF∥AC交BC于点F.若□ABCD的面积16cm2,AB=4cm,则△EBC的面积为__________,△CFG的面积为__________,△AGF的面积为_____________,GF= ______cm.
(第5题图) (第6题图) (第7题图)
7.如图,在□ABCD中,DE是∠ADC的平分线,F是AB的中点,AB=4,BC=6,则BE∶EF∶FC=__________.
8.□ABCD中,对角线AC,BD交于点O,若AB=6,AC=10,则BD的长的取值范围为____________________.
9.已知任意直线把.□ABCD分成两部分,要使这两部分的面积相等,直线所在的位置需满足的条件是
________________________________________________________
10.如图 在中,,点,,分别在,,上,四边形为平行四边形,,□ABCD的周长是_____________
11.已知点在面积为4的平行四边形的边上运动,使的面积为1的点共有 个.
12.在平面直角坐标系中,点的坐标分别为.若四边形为平行四边形,那么点的坐标是 .
二。选择题(3×8)
13.下列图案中,不是中心对称图形的是( )
14.下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是( )
A B C D
15.如图,在□ABCD中,,,与交于点,则该图中的平行四边形的个数共有 ( )
A.个 B.个 C.个 D.个
16 如图,平行四边形中,对角线相交于点,将平移至的位置,则图中与相等的其他线段有( )
A.1条 B.2条 C.3条 D.4条
17.如图,在□ABCD中,对角线相交于点,是对角线上的两点,当满足下列哪个条件时,四边形不一定是是平行四边形( )
A. B.
C. D.
18.,平行四边形中,,,的垂直平分线交于,则的周长是( )
A.6 B.8 C.9 D.10
19,在□ABCD中,,平分交边于点,则线段的长度分别为( )
A.和 B.和 C.和 D.和
20..□ABCD的周长是,的周长是,则的长为( )
A. B. C. D.
三.解答及证明(48分)
21.已知:如图,在四边形中,与相交于点,,.
求证:四边形是平行四边形.(6分)
22.在□ABCD中,已知AC、BD相交于点O,两条对角线的和为30cm,△OCD的周长为20cm,求AB的长.(6分)
23.如图,四边形ABCD中,AD∥BC,OE=OF,OA=OC,问四边形ABCD是平行四边形吗?为什么?(8分)
24.已知:如图,AC是平行四边形ABCD的对角线,MN∥AC,分别交DA、DC于M、N,交AB、BC的延长线于点P、Q.求证:MQ=PN.(8分)
25.在等腰△ABC中,AB=AC,点D是直线BC上一点,DE∥AC交直线AB于E,DF∥AB交直线AC于点F,解答下列各问:
(1)如图1,当点D在线段BC上时,有DE+DF=AB,请你说明理由;(6分)
(2)如图2,当点D在线段BC的延长线上时,请你参考(1)画出正确的图形,并写出线段DE、DF、AB之间的关系.(4分)
(图1) (图2)
26.(10分) 已知任意四边形,且线段、、、、、的中点分别是、、、、、.
(1)若四边形如图①,判断下列结论是否正确(正确的在括号里填“√”,错误的在括号里填“×”).
甲:顺次连接、、、一定得到平行四边形;( )
乙:顺次连接、、、一定得到平行四边形.( )
(2)请选择甲、乙中的一个,证明你对它的判断.
(3)若四边形如图②,请你判断(1)中的两个结论是否成立?
附加题. 如图,已知四边形纸片,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片.如果限定裁剪线最多有两条,能否做到: (用“能”或“不能”填空).若填“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.
A
B
C
D
中点
中点
中点
D
H
C
F
O
E
A
G
B
A
B
C
D
O
图②
A
D
C
B
F
B
E
A
D
C
H
P
图①
G
Q
A
B
C
D
