函数的奇偶性
图片预览





文档简介
课件16张PPT。数与形 本是相倚依
焉能分作两边飞
数无形时少直觉
形少数时难入微
数形结合百般好
隔离分家万事休
切莫忘 几何代数统一体
永远联系莫分离
—— 华罗庚
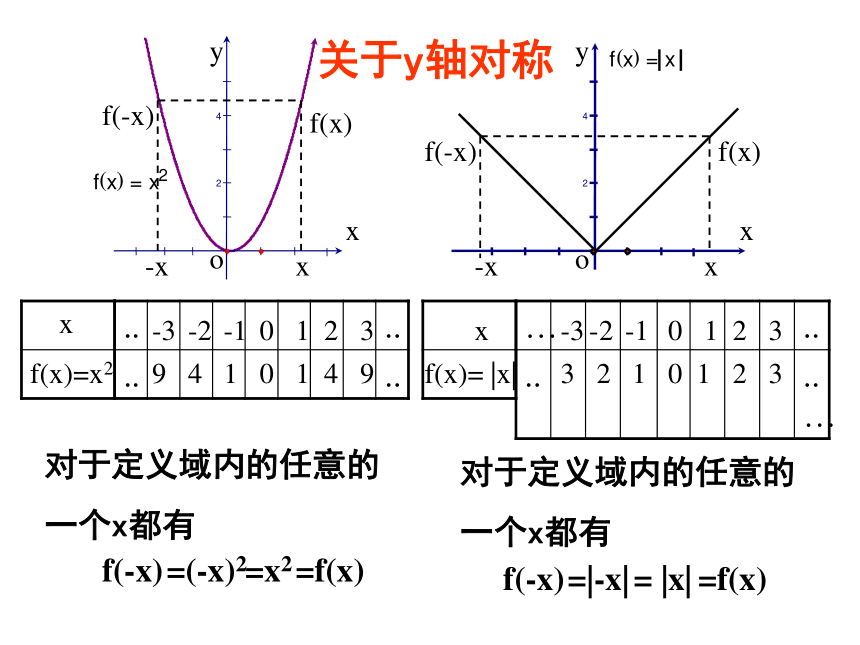
函数的奇偶性fx() = x242xyooyf(x)=x2x0x-x-xxxf(x)= |x|09900f(-x)f(-x)f(x)f(x)对于定义域内的任意的
一个x都有f(-x)=f(x)=(-x)2=x2关于y轴对称对于定义域内的任意的
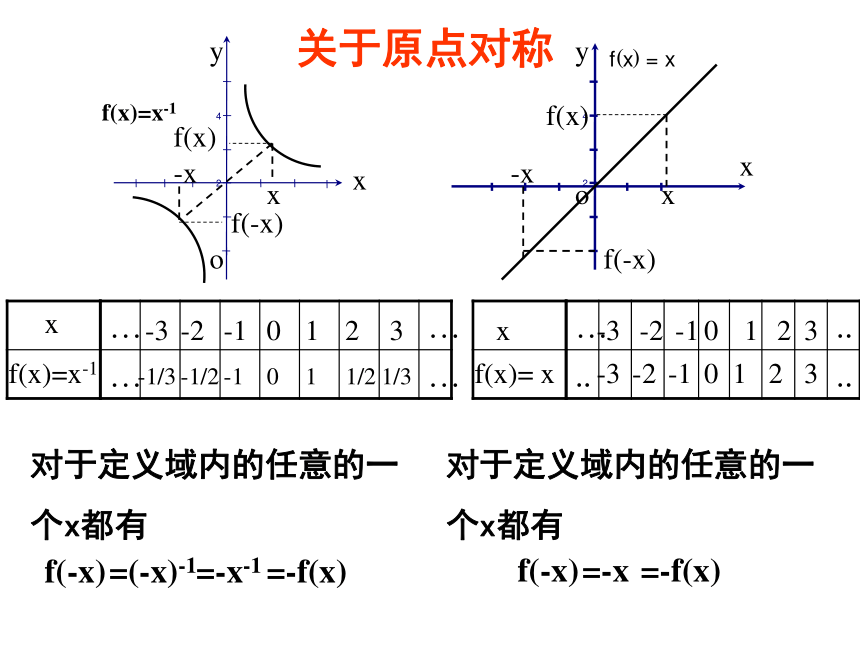
一个x都有f(-x) =f(x)=|-x| = |x|偶函数的定义:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)= f(x),那么函数f(x)就叫做偶函数.1) 定义域关于原点对称2) x是任意的4) 图象关于y轴对称3) 偶函数f(-x)= f(x)42xyooy42xf(x)=x-1x0x-x-xxxf(x)= x0-1/31/300f(-x)f(-x)f(x)f(x)对于定义域内的任意的一
个x都有f(-x)=-f(x)=(-x)-1 =-x-1关于原点对称对于定义域内的任意的一
个x都有f(-x) =-f(x)=-xf(x)=x-1奇函数的定义:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)= -f(x),那么函数f(x)就叫做奇函数.1) 定义域关于原点对称2) x是任意的4) 图象关于原点对称3) 奇函数f(-x)=- f(x)函数的奇偶性f(-x)= -f(x)奇函数偶函数f(-x)= f(x)关于y轴对称图象关于原点对称表达式名 称1)定义域关于原点对称
2) x是任意的f(-x) +f(x) = 0恒等变形f(-x) -f(x) = 0f(x) = f(-x)f(x) = -f(-x)注意例1、判断下列函数的奇偶性1) f(x)=|x+1|+|x-1|1)对于函数f(x)=|x+1|+|x-1| ,解:其定义域为(-∞,+∞),因为对定义域内的每一个x都有f(-x)= |-x+1|+|-x-1|所以函数为偶函数= |x-1| + |x+1|= f(x)f(x)=0 4) f(x)=lg|x|6) f(x)=3x1)求函数的定义域2)找出f(x)与 f(-x)的关系说明:练习2、已知f(x)是偶函数g(x)是奇函数,试将下图补充完整f(x)g(x)例2、已知函数f(x)是定义在R上的奇函数,当x≥o时,f(x)=x(1+x).画出函数f(x)的图象并求出函数f(x)的解析式解:设 x 0=-(-x)[1+(-x)]=x(1-x)也就是: f(x) =x(1-x) x< o x(1+x) x≥ o练习3、已知函数f(x)是定义在R上的偶函数,当x≤o时,f(x)=x2-3x, 求出函数f(x)的解析式解:小 结3、奇偶性的应用2、奇偶性的判断1、奇偶性的定义探究:若函数f(x)是 偶函数、 g(x)为 奇函数,那么f(x) g(x)是奇函数还是偶函数?奇函数奇偶性相同是偶函数奇偶性相反是奇函数结论:作业:P39、3练习3:已知函数y=f(x)及函数y=g(x)的图象分别如图(1)(2)所示,则函数y=f(x) g(x)的图象大致是( )ADCBB(2)(1)y=g(x)y=f(x)谢谢
焉能分作两边飞
数无形时少直觉
形少数时难入微
数形结合百般好
隔离分家万事休
切莫忘 几何代数统一体
永远联系莫分离
—— 华罗庚
函数的奇偶性fx() = x242xyooyf(x)=x2x0x-x-xxxf(x)= |x|09900f(-x)f(-x)f(x)f(x)对于定义域内的任意的
一个x都有f(-x)=f(x)=(-x)2=x2关于y轴对称对于定义域内的任意的
一个x都有f(-x) =f(x)=|-x| = |x|偶函数的定义:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)= f(x),那么函数f(x)就叫做偶函数.1) 定义域关于原点对称2) x是任意的4) 图象关于y轴对称3) 偶函数f(-x)= f(x)42xyooy42xf(x)=x-1x0x-x-xxxf(x)= x0-1/31/300f(-x)f(-x)f(x)f(x)对于定义域内的任意的一
个x都有f(-x)=-f(x)=(-x)-1 =-x-1关于原点对称对于定义域内的任意的一
个x都有f(-x) =-f(x)=-xf(x)=x-1奇函数的定义:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)= -f(x),那么函数f(x)就叫做奇函数.1) 定义域关于原点对称2) x是任意的4) 图象关于原点对称3) 奇函数f(-x)=- f(x)函数的奇偶性f(-x)= -f(x)奇函数偶函数f(-x)= f(x)关于y轴对称图象关于原点对称表达式名 称1)定义域关于原点对称
2) x是任意的f(-x) +f(x) = 0恒等变形f(-x) -f(x) = 0f(x) = f(-x)f(x) = -f(-x)注意例1、判断下列函数的奇偶性1) f(x)=|x+1|+|x-1|1)对于函数f(x)=|x+1|+|x-1| ,解:其定义域为(-∞,+∞),因为对定义域内的每一个x都有f(-x)= |-x+1|+|-x-1|所以函数为偶函数= |x-1| + |x+1|= f(x)f(x)=0 4) f(x)=lg|x|6) f(x)=3x1)求函数的定义域2)找出f(x)与 f(-x)的关系说明:练习2、已知f(x)是偶函数g(x)是奇函数,试将下图补充完整f(x)g(x)例2、已知函数f(x)是定义在R上的奇函数,当x≥o时,f(x)=x(1+x).画出函数f(x)的图象并求出函数f(x)的解析式解:设 x
