8.3实际问题与二元一次方程组同步课件
文档属性
| 名称 | 8.3实际问题与二元一次方程组同步课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 656.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-26 00:00:00 | ||
图片预览




文档简介
课件19张PPT。人教版七年级数学下册
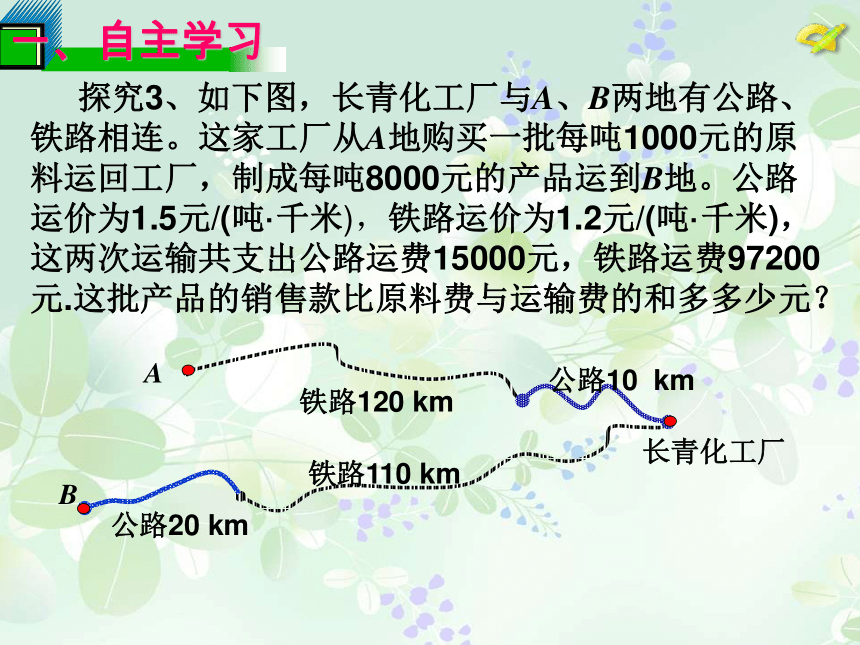
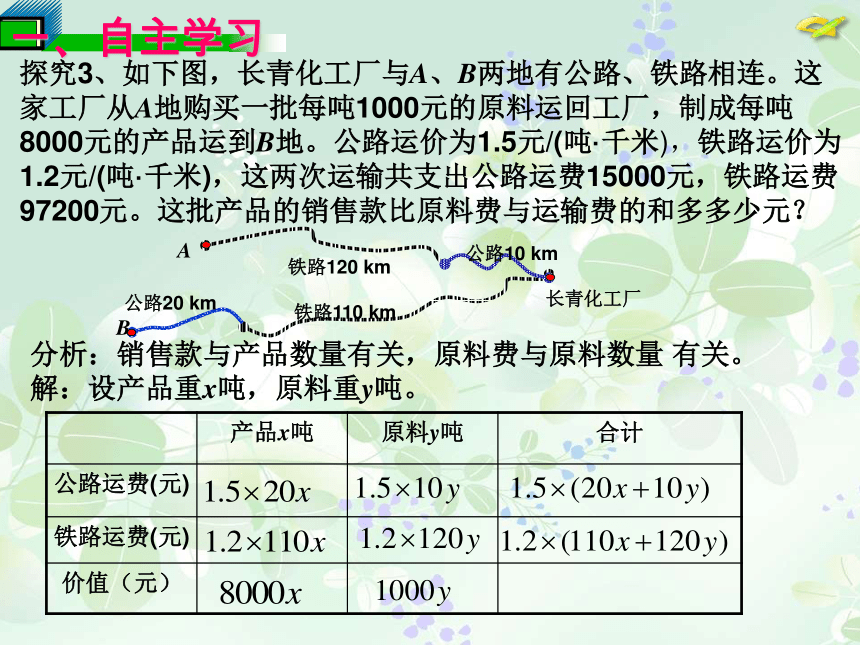
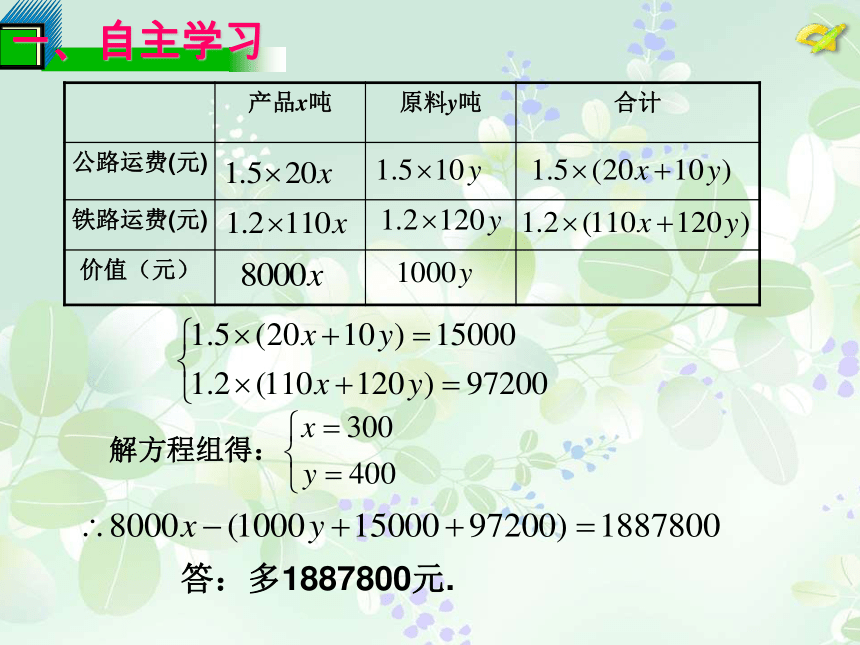
第八章 二元一次方程组8.3实际问题与二元一次方程组(3)本课内容实际问题与二元一次方程组 探究3、如下图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?探究3、如下图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?分析:销售款与产品数量有关,原料费与原料数量 有关。解:设产品重x吨,原料重y吨。解方程组得:答:多1887800元. 1.某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元,若制成奶片销售,每吨可获利润2000元.该厂生产能力如下:每天可加工3吨酸奶或1吨奶片,受人员和季节的限制,两种方式不能同时进行.受季节的限制,这批牛奶必须在4天内加工并销售完毕,为此该厂制定了两套方案:方案一:尽可能多的制成奶片,其余直接销售现牛奶方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成(1)你认为哪种方案获利最多,为什么? (2)本题解出之后,你还能提出哪些问题?其余5吨直接销售,获利500×5=2500(元) ∴共获利:8000+2500=10500(元)方案二:设生产奶片用x天,生 产酸奶用y天另:设x吨鲜奶制成奶片,y吨鲜奶制成酸奶方案一:生产奶片4天,共制成4吨奶片,获利 2000×4=80002、小亮跟爸爸于9月和10月初两次到超市购买食品.
9月份: 买6袋牛奶,12个面包,用30元.
10月初: 国庆酬宾,一律七五折优惠,比上次多买了4袋牛奶和3个面包.问题:找出等量关系并且列方程或方程组根据打折前后花30元所购买的物品数量,你能求出打折前牛奶和面包的单价个是多少吗? 2、小亮跟爸爸于9月和10月初两次到超市购买食品.
9月份: 买6袋牛奶,12个面包,用30元.
10月初: 国庆酬宾,一律七五折优惠,比上次多买了4袋牛奶和3个面包.根据打折前后花30元所购买的物品数量,你能求出打折前牛奶和面包的单价个是多少吗? 3、水资源透支令人担忧,节约用水迫在眉睫,针对居民用水浪费现象,某城市制定了每月用水标准8立方米,超标部分加价收费,某户居民连续两个月的用水和水费分别为12立方米、22元,10立方米,16.2元,试求这个城市的用水标准. 说明:即8立方米以内多少元/立方米,超过部分多少元/立方米3、水资源透支令人担忧,节约用水迫在眉睫,针对居民用水浪费现象,某城市制定了每月用水标准8立方米,超标部分加价收费,某户居民连续两个月的用水和水费分别为12立方米、22元,10立方米,16.2元,试求这个城市的用水标准.解:设8立方米以内每立方米x元,超过部分每立方米y元.答:8立方米以内每立方米2.3元,超过部分每立方米2.9元.4.红太阳大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元)。为吸引客源,在五一黄金周期间进行优惠大酬宾,凡团体入住一律五折优惠。一个50人的旅游团在五月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元。
①则三人间、双人间普通客房各住了多少间?
②如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么? 解:(1)设x人入住三人间,y人入住二人间.答:有24人入住三人间,26人入住二人间.(2)这种住宿方式不是费用最少的住宿方式,最少的住宿方式是48人入住三个间,2人入住二人间,最少费用为1270元.1、找等量关系是列方程组的关键和难点,有如下规律和方法:
(1)确定应用问题的类型,按其一般规律方法找等量关系;
(2)将问题中给出的条件按意思分割成两个方面,有“;”时一般“;”前后各一层,分别找出两个等量关系;
(3)借助表格提供的信息,按横向或纵向去分别打等量关系;
(4)图形问题,分析图形的长、宽,从中找等量关系.
2、设元时,一般采用直接设元,较复杂的采用间接设元,可化解难度,但无论怎样设元,设几个未知数,就要列几个方程.1、某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同.安全检查中,对4道门进行了测试:当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生;当同时开启一道正门和一道侧门时,4分钟内可以通过800名学生.
(1)求一道正门和一道侧门平均每分钟各可以通过多少名学生.
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低20%,安全检查规定在紧急情况下全大楼的学生应在5分钟内通过这4道门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问建造的这4道门是否符合安全规定?请说明理由. 2、某商场计划拨款9万元从厂家购进50台电视机.已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号的电视机的方案中,为使销售时获利最多,你选择哪种进货方案?再见
第八章 二元一次方程组8.3实际问题与二元一次方程组(3)本课内容实际问题与二元一次方程组 探究3、如下图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?探究3、如下图,长青化工厂与A、B两地有公路、铁路相连。这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?分析:销售款与产品数量有关,原料费与原料数量 有关。解:设产品重x吨,原料重y吨。解方程组得:答:多1887800元. 1.某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获利润500元,若制成酸奶销售,每吨可获利润1200元,若制成奶片销售,每吨可获利润2000元.该厂生产能力如下:每天可加工3吨酸奶或1吨奶片,受人员和季节的限制,两种方式不能同时进行.受季节的限制,这批牛奶必须在4天内加工并销售完毕,为此该厂制定了两套方案:方案一:尽可能多的制成奶片,其余直接销售现牛奶方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成(1)你认为哪种方案获利最多,为什么? (2)本题解出之后,你还能提出哪些问题?其余5吨直接销售,获利500×5=2500(元) ∴共获利:8000+2500=10500(元)方案二:设生产奶片用x天,生 产酸奶用y天另:设x吨鲜奶制成奶片,y吨鲜奶制成酸奶方案一:生产奶片4天,共制成4吨奶片,获利 2000×4=80002、小亮跟爸爸于9月和10月初两次到超市购买食品.
9月份: 买6袋牛奶,12个面包,用30元.
10月初: 国庆酬宾,一律七五折优惠,比上次多买了4袋牛奶和3个面包.问题:找出等量关系并且列方程或方程组根据打折前后花30元所购买的物品数量,你能求出打折前牛奶和面包的单价个是多少吗? 2、小亮跟爸爸于9月和10月初两次到超市购买食品.
9月份: 买6袋牛奶,12个面包,用30元.
10月初: 国庆酬宾,一律七五折优惠,比上次多买了4袋牛奶和3个面包.根据打折前后花30元所购买的物品数量,你能求出打折前牛奶和面包的单价个是多少吗? 3、水资源透支令人担忧,节约用水迫在眉睫,针对居民用水浪费现象,某城市制定了每月用水标准8立方米,超标部分加价收费,某户居民连续两个月的用水和水费分别为12立方米、22元,10立方米,16.2元,试求这个城市的用水标准. 说明:即8立方米以内多少元/立方米,超过部分多少元/立方米3、水资源透支令人担忧,节约用水迫在眉睫,针对居民用水浪费现象,某城市制定了每月用水标准8立方米,超标部分加价收费,某户居民连续两个月的用水和水费分别为12立方米、22元,10立方米,16.2元,试求这个城市的用水标准.解:设8立方米以内每立方米x元,超过部分每立方米y元.答:8立方米以内每立方米2.3元,超过部分每立方米2.9元.4.红太阳大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元)。为吸引客源,在五一黄金周期间进行优惠大酬宾,凡团体入住一律五折优惠。一个50人的旅游团在五月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元。
①则三人间、双人间普通客房各住了多少间?
②如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么? 解:(1)设x人入住三人间,y人入住二人间.答:有24人入住三人间,26人入住二人间.(2)这种住宿方式不是费用最少的住宿方式,最少的住宿方式是48人入住三个间,2人入住二人间,最少费用为1270元.1、找等量关系是列方程组的关键和难点,有如下规律和方法:
(1)确定应用问题的类型,按其一般规律方法找等量关系;
(2)将问题中给出的条件按意思分割成两个方面,有“;”时一般“;”前后各一层,分别找出两个等量关系;
(3)借助表格提供的信息,按横向或纵向去分别打等量关系;
(4)图形问题,分析图形的长、宽,从中找等量关系.
2、设元时,一般采用直接设元,较复杂的采用间接设元,可化解难度,但无论怎样设元,设几个未知数,就要列几个方程.1、某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同.安全检查中,对4道门进行了测试:当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生;当同时开启一道正门和一道侧门时,4分钟内可以通过800名学生.
(1)求一道正门和一道侧门平均每分钟各可以通过多少名学生.
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低20%,安全检查规定在紧急情况下全大楼的学生应在5分钟内通过这4道门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问建造的这4道门是否符合安全规定?请说明理由. 2、某商场计划拨款9万元从厂家购进50台电视机.已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号的电视机的方案中,为使销售时获利最多,你选择哪种进货方案?再见
