2023—2024学年人教版数学七年级上册4.1.2点、线、面、体课件(26张ppt)
文档属性
| 名称 | 2023—2024学年人教版数学七年级上册4.1.2点、线、面、体课件(26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
01情境导入
02问题导探
03典例导练
04小结导构
问题:物体的构成往往包含多种元素,几何图形也是如此.观察长方体模型,它有几个面?面与面相交的地方形成了几条线?线与线相交成几个点?
三棱柱呢?
01情境导入
02问题导探
03典例导练
04小结导构
观察可知:长方体有____个面,面与面相交的地方形成了_____条线,线与线相交成_____个点;三棱柱有_____个面,面与面相交的地方形成了____条线,线与线相交成____个点.
6
12
8
5
9
6
归纳:图形的构成元素包括___、 ___、 ___、 ___.
点
线
面
体
4.1.2 点、线、面、体
02问题导探
01情境导入
03典例导练
04小结导构
观察这些立体图形的各个面,它们有区别吗?
面是有区别的,可以分为平面和曲面;围成体的面只是平面或曲面的一部分.
03典例导练
01情境导入
02问题导探
04小结导构
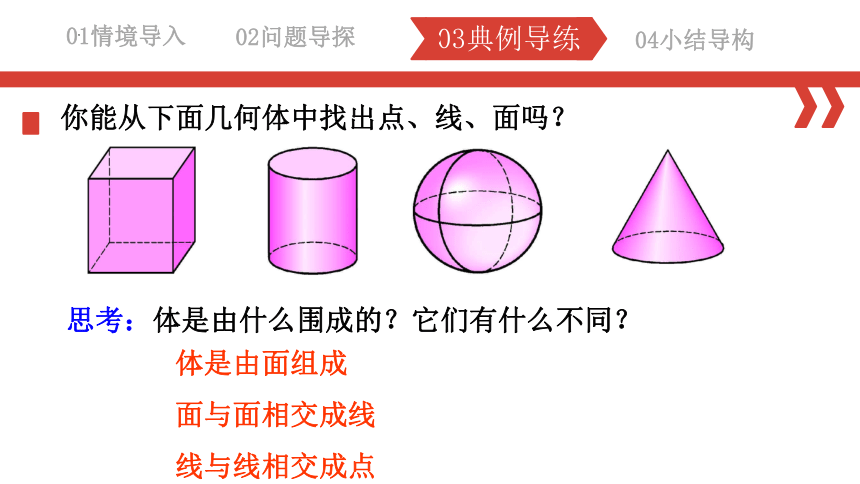
你能从下面几何体中找出点、线、面吗?
思考:体是由什么围成的?它们有什么不同?
体是由面组成
面与面相交成线
线与线相交成点
02问题导探
01情境导入
03典例导练
04小结导构
1.点、线、面、体的关系:几何体简称体,包围着体的是面,面和面相交的地方形成线,线和线相交的地方形成点.
2.几何图形都是由点、线、面、体组成的,点是构成图形的基本元素.
一、图形的构成元素及关系
01情境导入
04小结导构
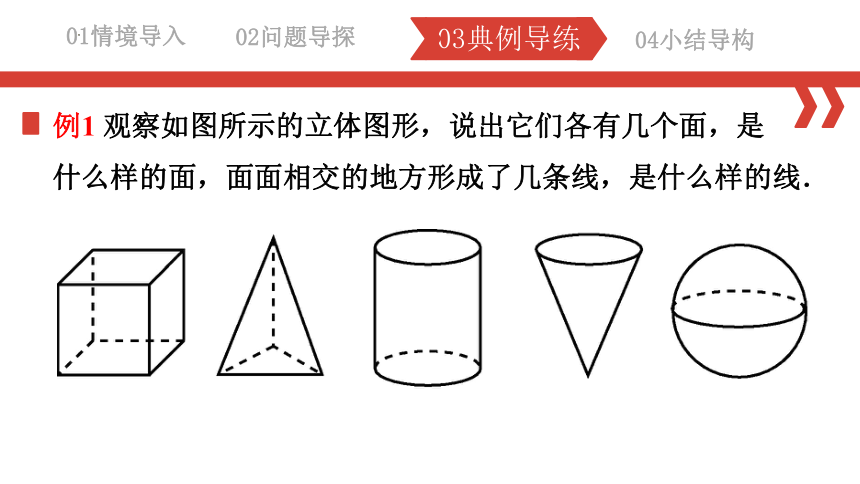
例1 观察如图所示的立体图形,说出它们各有几个面,是 什么样的面,面面相交的地方形成了几条线,是什么样的线.
03典例导练
02问题导探
03典例导练
01情境导入
02问题导探
04小结导构
解:①正方体有6个平面,面面相交形成12条线, 都是直的;②三棱锥有4个平面,面面相交形成6条线,都是直的;③圆柱有3个面,2个平面和1个曲面,面面相交形成2条曲线;④圆锥有2个面,1个平面和1个曲面,面面相交形成1条曲线;⑤球只有1个曲面.
03典例导练
01情境导入
02问题导探
04小结导构
练1-1 下面几何体中,全是由曲面围成的是( )
A.圆锥 B.正方体
C.圆柱 D.球
练1-2 在球、圆锥、圆柱、棱柱中,由曲面和平面围成的
是( )
A.球和圆锥 B.球和圆柱
C.圆锥和圆柱 D.圆柱和棱柱
D
C
02问题导探
01情境导入
03典例导练
04小结导构
二、曲面几何的形成方法
这可以说成:点动成线.
笔尖可以看作是一个点,这个点在纸上运动时,形成了什么?
02问题导探
01情境导入
03典例导练
04小结导构
举出生活中能够说明“点动成线”这一结论的例子.
02问题导探
01情境导入
03典例导练
04小结导构
汽车的雨刷在挡风玻璃上画出一个扇面,从几何的角度观察这种现象,你可以得出什么结论?
线动成面.
概括结论:
02问题导探
01情境导入
03典例导练
04小结导构
既然“点动成线,线动成面”,那么请同学们想一想:当面运动时又会形成什么图形?如何验证
你的猜想?
概括结论:
面动成体.
03典例导练
01情境导入
02问题导探
04小结导构
例2 笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;车轮旋转时,看起来像一个整体的圆面,这说明了__________;直角三角形绕它的一条直角边所在的直线旋转一周,形成了一个圆锥,这说明了_________.
点动成线
线动成面
面动成体
03典例导练
01情境导入
02问题导探
04小结导构
练2 把一张纸折叠,展开后得到一条折痕,这个现象
用数学知识可解释为( )
A.面与面相交成线
B.线动成面
C.面动成体
D.点动成线
A
02问题导探
01情境导入
03典例导练
04小结导构
点 线 面 体
点动成线
面动成体
线动成面
线与线相交形成点
面与面相交形成线
包围着体的部分是面
02问题导探
01情境导入
03典例导练
04小结导构
点、线、面、体与几何图形关系:
静态:面面相交——线,线线相交——点,
动态:点动成线,线动成面,面动成体.
02问题导探
01情境导入
03典例导练
04小结导构
02问题导探
01情境导入
03典例导练
04小结导构
一个平面图形旋转后得到一个立体图形,这个立体图形的形状取决于两个因素:
(1)平面图形的形状;
(2)旋转时所绕的轴的位置.
03典例导练
01情境导入
02问题导探
04小结导构
例3 如图,第一行的
图形绕轴旋转一周,
便能形成第二行的某个
几何体,请用直线对应
连接起来.
03典例导练
01情境导入
02问题导探
04小结导构
练3 如图所示的几何体是由哪个图形绕虚线旋转一周形成的( )
A
03典例导练
01情境导入
02问题导探
04小结导构
1. 下雨时,司机会打开雨刷器,雨刷器在运动时会
形成一个扇面,这是因为( )
A.点动成线
B.线动成面
C.面动成体
D.面面相交形成线
B
当堂练习
03典例导练
01情境导入
02问题导探
04小结导构
2. 下列现象能说明“面动成体”的是( )
A.时钟的钟摆摆动的轨迹
B.旋转一扇门,门在空中运动的轨迹
C.扔出一个小粉笔头,在天空中飞行的路线
D.打枪时子弹的轨迹
B
03典例导练
01情境导入
02问题导探
04小结导构
3. 现有一个长为5cm,宽为4cm的矩形,分别绕它的长、宽
所在的直线旋转一周,得到不同的圆柱体,他们的体积分别
是多少?谁的体积大?你得到什么启示?
03典例导练
01情境导入
02问题导探
04小结导构
4. 下列图形中,图(a)是正方体木块,把它切去一块,可以得到如图(b)(c)(d)(e).
(1) 我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入右表;
(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.
01情境导入
02问题导探
04小结导构
03典例导练
本节课你收获了什么?
01情境导入
02问题导探
03典例导练
04小结导构
问题:物体的构成往往包含多种元素,几何图形也是如此.观察长方体模型,它有几个面?面与面相交的地方形成了几条线?线与线相交成几个点?
三棱柱呢?
01情境导入
02问题导探
03典例导练
04小结导构
观察可知:长方体有____个面,面与面相交的地方形成了_____条线,线与线相交成_____个点;三棱柱有_____个面,面与面相交的地方形成了____条线,线与线相交成____个点.
6
12
8
5
9
6
归纳:图形的构成元素包括___、 ___、 ___、 ___.
点
线
面
体
4.1.2 点、线、面、体
02问题导探
01情境导入
03典例导练
04小结导构
观察这些立体图形的各个面,它们有区别吗?
面是有区别的,可以分为平面和曲面;围成体的面只是平面或曲面的一部分.
03典例导练
01情境导入
02问题导探
04小结导构
你能从下面几何体中找出点、线、面吗?
思考:体是由什么围成的?它们有什么不同?
体是由面组成
面与面相交成线
线与线相交成点
02问题导探
01情境导入
03典例导练
04小结导构
1.点、线、面、体的关系:几何体简称体,包围着体的是面,面和面相交的地方形成线,线和线相交的地方形成点.
2.几何图形都是由点、线、面、体组成的,点是构成图形的基本元素.
一、图形的构成元素及关系
01情境导入
04小结导构
例1 观察如图所示的立体图形,说出它们各有几个面,是 什么样的面,面面相交的地方形成了几条线,是什么样的线.
03典例导练
02问题导探
03典例导练
01情境导入
02问题导探
04小结导构
解:①正方体有6个平面,面面相交形成12条线, 都是直的;②三棱锥有4个平面,面面相交形成6条线,都是直的;③圆柱有3个面,2个平面和1个曲面,面面相交形成2条曲线;④圆锥有2个面,1个平面和1个曲面,面面相交形成1条曲线;⑤球只有1个曲面.
03典例导练
01情境导入
02问题导探
04小结导构
练1-1 下面几何体中,全是由曲面围成的是( )
A.圆锥 B.正方体
C.圆柱 D.球
练1-2 在球、圆锥、圆柱、棱柱中,由曲面和平面围成的
是( )
A.球和圆锥 B.球和圆柱
C.圆锥和圆柱 D.圆柱和棱柱
D
C
02问题导探
01情境导入
03典例导练
04小结导构
二、曲面几何的形成方法
这可以说成:点动成线.
笔尖可以看作是一个点,这个点在纸上运动时,形成了什么?
02问题导探
01情境导入
03典例导练
04小结导构
举出生活中能够说明“点动成线”这一结论的例子.
02问题导探
01情境导入
03典例导练
04小结导构
汽车的雨刷在挡风玻璃上画出一个扇面,从几何的角度观察这种现象,你可以得出什么结论?
线动成面.
概括结论:
02问题导探
01情境导入
03典例导练
04小结导构
既然“点动成线,线动成面”,那么请同学们想一想:当面运动时又会形成什么图形?如何验证
你的猜想?
概括结论:
面动成体.
03典例导练
01情境导入
02问题导探
04小结导构
例2 笔尖在纸上快速滑动写出了一个又一个字,这说明了_________;车轮旋转时,看起来像一个整体的圆面,这说明了__________;直角三角形绕它的一条直角边所在的直线旋转一周,形成了一个圆锥,这说明了_________.
点动成线
线动成面
面动成体
03典例导练
01情境导入
02问题导探
04小结导构
练2 把一张纸折叠,展开后得到一条折痕,这个现象
用数学知识可解释为( )
A.面与面相交成线
B.线动成面
C.面动成体
D.点动成线
A
02问题导探
01情境导入
03典例导练
04小结导构
点 线 面 体
点动成线
面动成体
线动成面
线与线相交形成点
面与面相交形成线
包围着体的部分是面
02问题导探
01情境导入
03典例导练
04小结导构
点、线、面、体与几何图形关系:
静态:面面相交——线,线线相交——点,
动态:点动成线,线动成面,面动成体.
02问题导探
01情境导入
03典例导练
04小结导构
02问题导探
01情境导入
03典例导练
04小结导构
一个平面图形旋转后得到一个立体图形,这个立体图形的形状取决于两个因素:
(1)平面图形的形状;
(2)旋转时所绕的轴的位置.
03典例导练
01情境导入
02问题导探
04小结导构
例3 如图,第一行的
图形绕轴旋转一周,
便能形成第二行的某个
几何体,请用直线对应
连接起来.
03典例导练
01情境导入
02问题导探
04小结导构
练3 如图所示的几何体是由哪个图形绕虚线旋转一周形成的( )
A
03典例导练
01情境导入
02问题导探
04小结导构
1. 下雨时,司机会打开雨刷器,雨刷器在运动时会
形成一个扇面,这是因为( )
A.点动成线
B.线动成面
C.面动成体
D.面面相交形成线
B
当堂练习
03典例导练
01情境导入
02问题导探
04小结导构
2. 下列现象能说明“面动成体”的是( )
A.时钟的钟摆摆动的轨迹
B.旋转一扇门,门在空中运动的轨迹
C.扔出一个小粉笔头,在天空中飞行的路线
D.打枪时子弹的轨迹
B
03典例导练
01情境导入
02问题导探
04小结导构
3. 现有一个长为5cm,宽为4cm的矩形,分别绕它的长、宽
所在的直线旋转一周,得到不同的圆柱体,他们的体积分别
是多少?谁的体积大?你得到什么启示?
03典例导练
01情境导入
02问题导探
04小结导构
4. 下列图形中,图(a)是正方体木块,把它切去一块,可以得到如图(b)(c)(d)(e).
(1) 我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入右表;
(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.
01情境导入
02问题导探
04小结导构
03典例导练
本节课你收获了什么?
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
