2014-2015学年人教版选修3-3 第八章第2节:气体的等容变化和等压变化 课件(34张)
文档属性
| 名称 | 2014-2015学年人教版选修3-3 第八章第2节:气体的等容变化和等压变化 课件(34张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2015-04-20 18:56:12 | ||
图片预览











文档简介
课件35张PPT。2 气体的等容变化和等压变化一、气体的等容变化
1.等容变化:一定质量的某种气体,在体积不变时,_____随
_____的变化。
2.查理定律:
(1)内容:一定质量的某种气体,在体积不变的情况下,压强p
与热力学温度T成_____。压强温度正比(2)表达式:
①_____或_____(C是比例常数)。
②__________或__________(p1、T1和p2、T2分别表示1、2两
个不同状态下的压强和热力学温度)。
(3)图像:p=CT(4)适用条件:气体的_____一定,_____不变。
(5)查理定律是_____定律,是由法国科学家查理发现的。 质量体积实验二、气体的等压变化
1.等压变化:一定质量的某种气体,在压强不变的情况下,
_____随_____的变化。
2.盖—吕萨克定律:
(1)内容:一定质量的某种气体,在压强不变的情况下,其体
积V与热力学温度T成正比。
(2)表达式:
①_____或_____(C是比例常数)。
②__________或__________(V1、T1和V2、T2分别表示1、2两
个不同状态下的体积和热力学温度)。体积温度V=CT(3)图像:
(4)适用条件:气体_____一定,_____不变。
(5)盖—吕萨克定律是通过_____发现的。质量压强实验1.判一判
(1)在质量和体积不变的情况下,气体的压强与摄氏温度成
正比。( )
(2)一定质量的气体在压强不太大,温度不太低时,无论是
p -T图像还是V -T图像,都是一条过坐标原点的直线。( )
(3)气体在做等容变化时,温度升高1 ℃,增大的压强是原来
压强的 ( )
(4)pV=C、 三个公式中的常数C是同一个值。( )提示:(1)×。在质量和体积不变的情况下,气体的压强与热
力学温度成正比。
(2)√。在压强不太大,温度不太低时,等容线和等压线都是
过原点的直线。
(3)×。气体在做等容变化时,温度升高1 ℃,增大的压强是
0 ℃时压强的
(4)×。pV=C中的C与气体的质量、温度及气体种类有关,
中的C与质量、体积及气体种类有关, 中的C与质量、压强
及气体种类有关,所以三个C不是同一个值。2.想一想
某登山运动员在一次攀登珠穆朗玛峰的过程中,在接近山顶时他裸露在手腕上的防水手表的表盘玻璃突然爆裂了,而手表没有受到任何撞击,你知道其中的原因吗?
提示:手表表壳可以看成一个密闭容器,出厂时封闭着一定质量的气体,登山过程中气体发生等容变化,因为高山山顶附近的压强比山脚处小很多,内外压力差超过表盘玻璃的承受限度,便会发生爆裂。 主题一 探究气体的等容变化
1.在等容过程中,试回答下列问题:
(1)气体的压强p与摄氏温度t是不是成正比例关系?
(2)写出摄氏温标下查理定律的数学表达式。
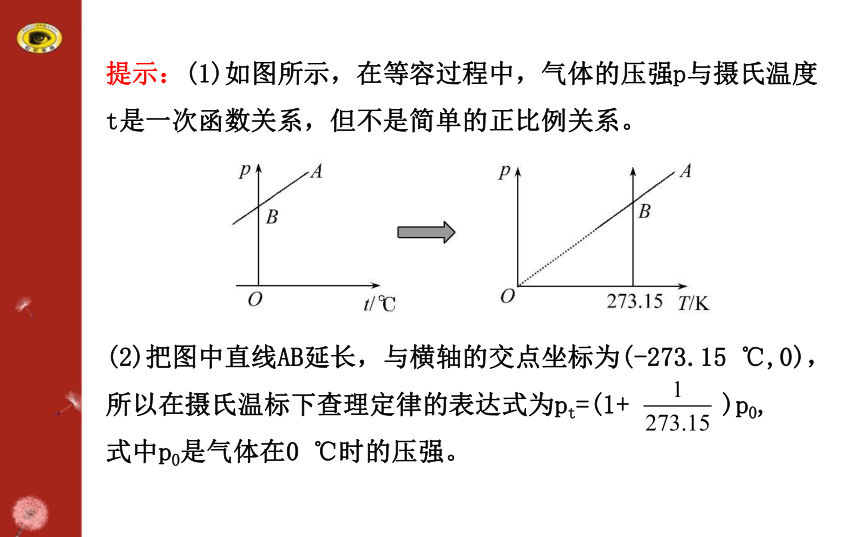
(3)在摄氏温标下应该怎样表述查理定律。提示:(1)如图所示,在等容过程中,气体的压强p与摄氏温度
t是一次函数关系,但不是简单的正比例关系。
(2)把图中直线AB延长,与横轴的交点坐标为(-273.15 ℃,0),
所以在摄氏温标下查理定律的表达式为pt=(1+ )p0,
式中p0是气体在0 ℃时的压强。(3)在摄氏温标下查理定律应该表述为:一定质量的某种气
体,在体积不变时,温度每升高(或降低)1 ℃,增大(或减
小)的压强等于它在0 ℃时压强的2.尝试根据等容线说明为什么绝对零度是低温的极限,只能接近,不能达到。
提示:在p -T坐标系中,等容线是一条延长线通过原点的倾斜直线,事实上,在温度很低时,查理定律已不适用了。由查理定律外推得出的结果表明,绝对零度时,气体压强为零,说明分子将停止运动,这是不可能的,所以,绝对零度是低温的极限,只能接近,不能达到。正因为如此,在p -T坐标系中画等容线时,原点附近一小段应画成虚线,表示它仅是外推的结果。3.如图为不同体积的气体的p -T图像和p -t图像,从图像来分析,等容线的斜率大小与气体体积的大小之间有怎样的对应关系?
提示:从图像可以看出,无论是p -T图像还是p -t图像,都是等容线的斜率越大,体积越小,因此,V1>V2。【知识点睛】查理定律的另一种表示
一定质量的某种气体从初状态(p、T)开始发生等容变化,
其压强的变化量Δp与温度的变化量ΔT之间的关系为:
Δp=【规律方法】利用查理定律解题的一般步骤
(1)确定研究对象,即被封闭的气体。
(2)分析被研究气体在状态变化时是否符合定律成立条件,即是否是质量和体积保持不变。
(3)确定初、末两个状态的温度、压强。
(4)按查理定律公式列式求解,并对结果进行讨论。【典例1】如图甲所示,容器A和B分别盛有氢气和氧气,用一段水平细玻璃管连通,管内有一段水银柱将两种气体隔开。当氢气的温度为0℃、氧气温度为20℃时,水银柱保持静止。判断下列情况下,水银柱将怎样移动?(1)两气体均升高20℃;
(2)氢气升高10℃,氧气升高20℃;
(3)若初状态如图乙所示且气体初温相同,则当两气体均降低10℃时,水银柱怎样移动?【解题探究】(1)由查理定律 得:
即Δp=________。
(2)对于图甲,氢气和氧气的初压强相同,设为p。当温度变
化时,先假设水银柱不动。根据温度变化后两部分气体压强
的变化_____________________。判断水银柱的移动情况【解析】(1)ΔpA= >0,ΔpB= >0
因为ΔpA>ΔpB,故水银柱向B容器一方移动。
(2)ΔpA= >0,ΔpB= >0
因为ΔpA<ΔpB,故水银柱向A容器一方移动。
(3)ΔpA= pA<0,ΔpB= pB<0
因为pA>pB,故|ΔpA|>|ΔpB|,水银柱向A容器一方(向下)移动。
答案:(1)向B移动 (2)向A移动 (3)向A(下)移动【变式训练】有人设计了一种测温装置,其结构如图
所示,玻璃泡A内封有一定量的气体,与A相连的B管插
在水槽中,管内水银面的高度x可反映泡内气体的温
度,即环境温度,并可由B管上的刻度直接读出。设B管
的体积与A玻璃泡的体积相比可忽略不计。在1标准大
气压下对B管进行温度刻度(1标准大气压相当于76cmHg的压强,等于101kPa)。已知当温度t1=27℃时,管内水银面高度x1=16cm,此高度即为27℃的刻度线,问t=0℃的刻度线在何处。【解析】选玻璃泡A内的气体为研究对象,由于B管的体积可略
去不计,所以在温度变化时,A内气体经历的是一个等容变化过
程。
玻璃泡A内气体的初状态:T1=300K,p1=(76-16)cmHg=60 cmHg
末状态:T0=273K,p=?
由查理定律
得:p= ×60 cmHg=54.6 cmHg
所以t=0℃时水银面高度,即刻度线的位置是x0=(76-54.6)cm=
21.4 cm。
答案:21.4cm主题二 探究气体的等压变化
1.一定质量的气体发生等压变化过程中,试回答下列问题:
(1)气体的体积V与摄氏温度t是不是正比例关系?
(2)写出摄氏温标下盖—吕萨克定律的数学表达式。
(3)在摄氏温标下应该怎样表述盖—吕萨克定律。提示:(1)在等压过程中,气体的体积V与摄氏温度t是一次函
数关系,但不是简单的正比例关系。
(2)在摄氏温标下盖—吕萨克定律的表达式为V=
式中V0是气体在0 ℃时的体积。
(3)在摄氏温标下盖—吕萨克定律应该表述为:一定质量的某
种气体,在压强不变时,温度每升高(或降低)1 ℃,增大(或
减小)的体积等于它在0 ℃时体积的2.如图为不同压强的气体的V -T图像和V-t图像,从图像来分析,等压线的斜率大小与气体压强大小之间有怎样的对应关系?
提示:从图像可以看出,无论是V -T图像还是V -t图像,都是等压线的斜率越大,压强越小,因此,p1>p2。【知识点睛】
(1)盖—吕萨克定律的另一种表示:一定质量的某种气体从初
状态(V、T)开始发生等压变化,其体积的变化量ΔV与温度的
变化量ΔT之间的关系为:ΔV=
(2)图像特点:p - 图像、p -T图像、V -T图像在原点附近
都要画成虚线。 【规律方法】利用盖—吕萨克定律解题的一般步骤
(1)确定研究对象,即被封闭气体。
(2)分析被研究气体在状态变化时是否符合定律成立条件,即是否是质量和压强保持不变。
(3)分别找出初、末两状态的温度、体积。
(4)根据盖—吕萨克定律列方程求解,并对结果进行讨论。【典例2】如图所示,一圆柱形容器竖直放置,
通过活塞封闭着摄氏温度为t的理想气体。活
塞的质量为m,横截面积为S,与容器底部相距h。
现通过电热丝给气体加热一段时间,结果活塞
缓慢上升了h,已知大气压强为p0,重力加速度为g,不计器壁向外散失的热量及活塞与器壁间的摩擦,求:
(1)气体的压强;
(2)这段时间内气体的温度升高了多少?【解题探究】(1)根据力的平衡pS=______。
(2)活塞缓慢上升的过程中被封闭的气体做_________。p0S+mg等压变化【解析】(1)以活塞为研究对象,受力分析得:
pS=p0S+mg
解得气体的压强为p=p0+
(2)以被封闭气体为研究对象,气体经历等压变化,初状态:V1=hS T1=273+t
末状态:V2=2hS T2=273+t′
由盖—吕萨克定律
得:
解得:t′=273+2t
Δt=t′-t=273+t。
答案:(1)p0+ (2)273+t【变式训练】如图所示,A汽缸中用活塞封闭有一定质量的理想气体,温度为27 ℃,活塞与汽缸底部距离为h,活塞截面积为S。汽缸中的活塞通过滑轮系统挂一重物,质量为m。若不计一切摩擦,当气体的温度升高10 ℃且系统稳定后,求重物m下降的高度。【解析】初、末状态,物块静止,可知绳中拉力大小相等,
分析活塞可知,气体发生等压变化。由盖—吕萨克定律知:
V1=Sh,ΔV=SΔh
T1=300 K,解得
答案:
1.等容变化:一定质量的某种气体,在体积不变时,_____随
_____的变化。
2.查理定律:
(1)内容:一定质量的某种气体,在体积不变的情况下,压强p
与热力学温度T成_____。压强温度正比(2)表达式:
①_____或_____(C是比例常数)。
②__________或__________(p1、T1和p2、T2分别表示1、2两
个不同状态下的压强和热力学温度)。
(3)图像:p=CT(4)适用条件:气体的_____一定,_____不变。
(5)查理定律是_____定律,是由法国科学家查理发现的。 质量体积实验二、气体的等压变化
1.等压变化:一定质量的某种气体,在压强不变的情况下,
_____随_____的变化。
2.盖—吕萨克定律:
(1)内容:一定质量的某种气体,在压强不变的情况下,其体
积V与热力学温度T成正比。
(2)表达式:
①_____或_____(C是比例常数)。
②__________或__________(V1、T1和V2、T2分别表示1、2两
个不同状态下的体积和热力学温度)。体积温度V=CT(3)图像:
(4)适用条件:气体_____一定,_____不变。
(5)盖—吕萨克定律是通过_____发现的。质量压强实验1.判一判
(1)在质量和体积不变的情况下,气体的压强与摄氏温度成
正比。( )
(2)一定质量的气体在压强不太大,温度不太低时,无论是
p -T图像还是V -T图像,都是一条过坐标原点的直线。( )
(3)气体在做等容变化时,温度升高1 ℃,增大的压强是原来
压强的 ( )
(4)pV=C、 三个公式中的常数C是同一个值。( )提示:(1)×。在质量和体积不变的情况下,气体的压强与热
力学温度成正比。
(2)√。在压强不太大,温度不太低时,等容线和等压线都是
过原点的直线。
(3)×。气体在做等容变化时,温度升高1 ℃,增大的压强是
0 ℃时压强的
(4)×。pV=C中的C与气体的质量、温度及气体种类有关,
中的C与质量、体积及气体种类有关, 中的C与质量、压强
及气体种类有关,所以三个C不是同一个值。2.想一想
某登山运动员在一次攀登珠穆朗玛峰的过程中,在接近山顶时他裸露在手腕上的防水手表的表盘玻璃突然爆裂了,而手表没有受到任何撞击,你知道其中的原因吗?
提示:手表表壳可以看成一个密闭容器,出厂时封闭着一定质量的气体,登山过程中气体发生等容变化,因为高山山顶附近的压强比山脚处小很多,内外压力差超过表盘玻璃的承受限度,便会发生爆裂。 主题一 探究气体的等容变化
1.在等容过程中,试回答下列问题:
(1)气体的压强p与摄氏温度t是不是成正比例关系?
(2)写出摄氏温标下查理定律的数学表达式。
(3)在摄氏温标下应该怎样表述查理定律。提示:(1)如图所示,在等容过程中,气体的压强p与摄氏温度
t是一次函数关系,但不是简单的正比例关系。
(2)把图中直线AB延长,与横轴的交点坐标为(-273.15 ℃,0),
所以在摄氏温标下查理定律的表达式为pt=(1+ )p0,
式中p0是气体在0 ℃时的压强。(3)在摄氏温标下查理定律应该表述为:一定质量的某种气
体,在体积不变时,温度每升高(或降低)1 ℃,增大(或减
小)的压强等于它在0 ℃时压强的2.尝试根据等容线说明为什么绝对零度是低温的极限,只能接近,不能达到。
提示:在p -T坐标系中,等容线是一条延长线通过原点的倾斜直线,事实上,在温度很低时,查理定律已不适用了。由查理定律外推得出的结果表明,绝对零度时,气体压强为零,说明分子将停止运动,这是不可能的,所以,绝对零度是低温的极限,只能接近,不能达到。正因为如此,在p -T坐标系中画等容线时,原点附近一小段应画成虚线,表示它仅是外推的结果。3.如图为不同体积的气体的p -T图像和p -t图像,从图像来分析,等容线的斜率大小与气体体积的大小之间有怎样的对应关系?
提示:从图像可以看出,无论是p -T图像还是p -t图像,都是等容线的斜率越大,体积越小,因此,V1>V2。【知识点睛】查理定律的另一种表示
一定质量的某种气体从初状态(p、T)开始发生等容变化,
其压强的变化量Δp与温度的变化量ΔT之间的关系为:
Δp=【规律方法】利用查理定律解题的一般步骤
(1)确定研究对象,即被封闭的气体。
(2)分析被研究气体在状态变化时是否符合定律成立条件,即是否是质量和体积保持不变。
(3)确定初、末两个状态的温度、压强。
(4)按查理定律公式列式求解,并对结果进行讨论。【典例1】如图甲所示,容器A和B分别盛有氢气和氧气,用一段水平细玻璃管连通,管内有一段水银柱将两种气体隔开。当氢气的温度为0℃、氧气温度为20℃时,水银柱保持静止。判断下列情况下,水银柱将怎样移动?(1)两气体均升高20℃;
(2)氢气升高10℃,氧气升高20℃;
(3)若初状态如图乙所示且气体初温相同,则当两气体均降低10℃时,水银柱怎样移动?【解题探究】(1)由查理定律 得:
即Δp=________。
(2)对于图甲,氢气和氧气的初压强相同,设为p。当温度变
化时,先假设水银柱不动。根据温度变化后两部分气体压强
的变化_____________________。判断水银柱的移动情况【解析】(1)ΔpA= >0,ΔpB= >0
因为ΔpA>ΔpB,故水银柱向B容器一方移动。
(2)ΔpA= >0,ΔpB= >0
因为ΔpA<ΔpB,故水银柱向A容器一方移动。
(3)ΔpA= pA<0,ΔpB= pB<0
因为pA>pB,故|ΔpA|>|ΔpB|,水银柱向A容器一方(向下)移动。
答案:(1)向B移动 (2)向A移动 (3)向A(下)移动【变式训练】有人设计了一种测温装置,其结构如图
所示,玻璃泡A内封有一定量的气体,与A相连的B管插
在水槽中,管内水银面的高度x可反映泡内气体的温
度,即环境温度,并可由B管上的刻度直接读出。设B管
的体积与A玻璃泡的体积相比可忽略不计。在1标准大
气压下对B管进行温度刻度(1标准大气压相当于76cmHg的压强,等于101kPa)。已知当温度t1=27℃时,管内水银面高度x1=16cm,此高度即为27℃的刻度线,问t=0℃的刻度线在何处。【解析】选玻璃泡A内的气体为研究对象,由于B管的体积可略
去不计,所以在温度变化时,A内气体经历的是一个等容变化过
程。
玻璃泡A内气体的初状态:T1=300K,p1=(76-16)cmHg=60 cmHg
末状态:T0=273K,p=?
由查理定律
得:p= ×60 cmHg=54.6 cmHg
所以t=0℃时水银面高度,即刻度线的位置是x0=(76-54.6)cm=
21.4 cm。
答案:21.4cm主题二 探究气体的等压变化
1.一定质量的气体发生等压变化过程中,试回答下列问题:
(1)气体的体积V与摄氏温度t是不是正比例关系?
(2)写出摄氏温标下盖—吕萨克定律的数学表达式。
(3)在摄氏温标下应该怎样表述盖—吕萨克定律。提示:(1)在等压过程中,气体的体积V与摄氏温度t是一次函
数关系,但不是简单的正比例关系。
(2)在摄氏温标下盖—吕萨克定律的表达式为V=
式中V0是气体在0 ℃时的体积。
(3)在摄氏温标下盖—吕萨克定律应该表述为:一定质量的某
种气体,在压强不变时,温度每升高(或降低)1 ℃,增大(或
减小)的体积等于它在0 ℃时体积的2.如图为不同压强的气体的V -T图像和V-t图像,从图像来分析,等压线的斜率大小与气体压强大小之间有怎样的对应关系?
提示:从图像可以看出,无论是V -T图像还是V -t图像,都是等压线的斜率越大,压强越小,因此,p1>p2。【知识点睛】
(1)盖—吕萨克定律的另一种表示:一定质量的某种气体从初
状态(V、T)开始发生等压变化,其体积的变化量ΔV与温度的
变化量ΔT之间的关系为:ΔV=
(2)图像特点:p - 图像、p -T图像、V -T图像在原点附近
都要画成虚线。 【规律方法】利用盖—吕萨克定律解题的一般步骤
(1)确定研究对象,即被封闭气体。
(2)分析被研究气体在状态变化时是否符合定律成立条件,即是否是质量和压强保持不变。
(3)分别找出初、末两状态的温度、体积。
(4)根据盖—吕萨克定律列方程求解,并对结果进行讨论。【典例2】如图所示,一圆柱形容器竖直放置,
通过活塞封闭着摄氏温度为t的理想气体。活
塞的质量为m,横截面积为S,与容器底部相距h。
现通过电热丝给气体加热一段时间,结果活塞
缓慢上升了h,已知大气压强为p0,重力加速度为g,不计器壁向外散失的热量及活塞与器壁间的摩擦,求:
(1)气体的压强;
(2)这段时间内气体的温度升高了多少?【解题探究】(1)根据力的平衡pS=______。
(2)活塞缓慢上升的过程中被封闭的气体做_________。p0S+mg等压变化【解析】(1)以活塞为研究对象,受力分析得:
pS=p0S+mg
解得气体的压强为p=p0+
(2)以被封闭气体为研究对象,气体经历等压变化,初状态:V1=hS T1=273+t
末状态:V2=2hS T2=273+t′
由盖—吕萨克定律
得:
解得:t′=273+2t
Δt=t′-t=273+t。
答案:(1)p0+ (2)273+t【变式训练】如图所示,A汽缸中用活塞封闭有一定质量的理想气体,温度为27 ℃,活塞与汽缸底部距离为h,活塞截面积为S。汽缸中的活塞通过滑轮系统挂一重物,质量为m。若不计一切摩擦,当气体的温度升高10 ℃且系统稳定后,求重物m下降的高度。【解析】初、末状态,物块静止,可知绳中拉力大小相等,
分析活塞可知,气体发生等压变化。由盖—吕萨克定律知:
V1=Sh,ΔV=SΔh
T1=300 K,解得
答案:
