3.3离心现象课件(共27张PPT)高一下学期物理鲁科版(2019)必修第二册
文档属性
| 名称 | 3.3离心现象课件(共27张PPT)高一下学期物理鲁科版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-11-29 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
第
节
3
离心现象
高中物理 必修第二册
第3章
1.学会通过车辆转弯问题及凹、凸桥和过山车问题分析水平面内和竖直面内的圆周运动。
2.知道什么是离心运动,学会通过实例分析离心运动。
3.学会运用圆周运动知识分析生活中的实际问题。
学习目标
思考:为什么在拐弯处容易发生事故?
应该如何避免这种事件的发生?
引入
汽车在水平地面上转弯时是什么力提供向心力的呢
O
mg
N
f
一、车辆转弯时所需的向心力
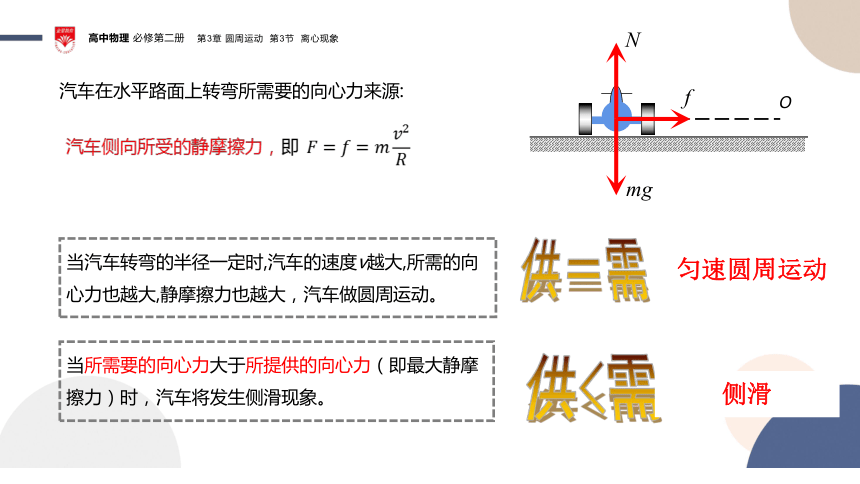
汽车在水平路面上转弯所需要的向心力来源:
当汽车转弯的半径一定时,汽车的速度v越大,所需的向心力也越大,静摩擦力也越大,汽车做圆周运动。
供=需
匀速圆周运动
供<需
侧滑
当所需要的向心力大于所提供的向心力(即最大静摩擦力)时,汽车将发生侧滑现象。
O
mg
N
f
赛道的设计
思考:火车转弯时是在做圆周运动,什么力提供向心力?
G
外轨
内轨
N
F
外轨对轮缘的弹力
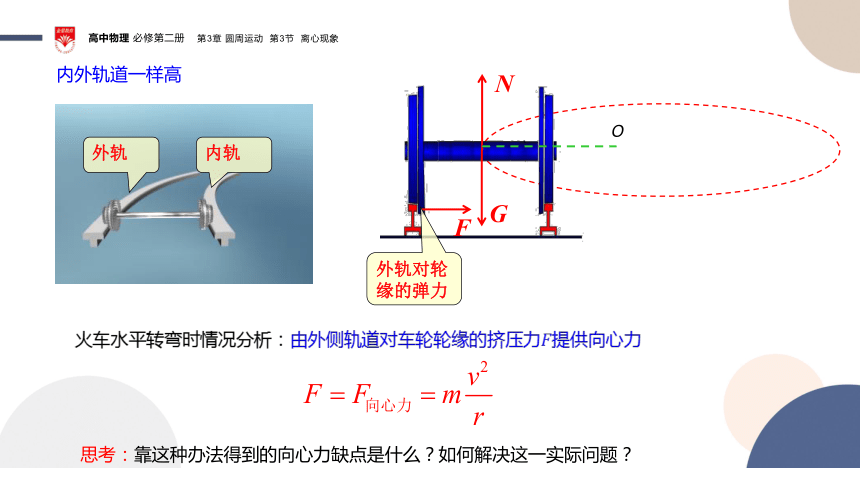
内外轨道一样高
O
火车水平转弯时情况分析:由外侧轨道对车轮轮缘的挤压力提供向心力
思考:靠这种办法得到的向心力缺点是什么?如何解决这一实际问题?
外轨高于内轨
在转弯处外轨略高于内轨
θ
N
G
O
F合
θ
火车转弯所需的向心力的方向是在水平方向上还是在与斜面平行的方向上?
轨道对轮缘无挤压,此时火车的速度为多大?
θ很小时,sinθ≈tanθ
若火车的速度大于或小于这个值时,轨道对轮缘有挤压吗?
2、当
1、当 :
G
N
θ
轮缘受到外轨向内的挤压力,外轨易损坏。
G
N
θ
F
F
轮缘受到内轨向外的挤压力,内轨易损坏。
思考:为什么桥的外形都是凸起的而没有凹陷的?
这样的设计跟向心力又有怎么样的关系呢?
二、竖直平面内的圆周运动分析
1.求汽车以速度过半径为 的拱桥最高点时对拱桥的压力?
【解】和的合力提供汽车做圆周运动的向心力,由牛顿第二定律得:
可见汽车的速度越大对桥的压力越小。
当 时汽车对桥的压力为零。(临界速度)
思考:当 大于时,汽车做什么运动?
汽车脱离桥面,做平抛运动。
N<mg,失重状态
2.求汽车过凹形路段最低点时对路面的压力?
【解】和的合力提供汽车做圆周运动的向心力,由牛顿第二定律得:
可见汽车的速度v越大,对桥的压力越大。
超重状态
若汽车通过凹桥的速度增大,会出现什么情况?
思考:过山车为什么在最高点也不会掉下来
讨论
物做近心运动
① 绳和内轨模型
理论研究
mg
N
v
轨道提供支持力,绳子提供拉力。
v
② 杆儿和双轨模型
能过最高点的临界条件:
当速度 > 时, 杆对小球是拉力;
当速度 < 时, 杆对小球是支持力;
当速度 = 时, 杆对小球无作用力。
mg
N
杆既可以提供拉力,也可以提供支持力。
N
当
向心力的“供求”关系——所需向心力与提供向心力;
思考:如果所需向心力与提供向心力大小不相等时物体将如何运动?
F合 = mω2r,
O
物体做匀速圆周运动
供=需
三、生活中的离心运动
O
F合 = mω2r,
F合<mω2r ,
F 合= 0 ,
1、定义:做匀速圆周运动的物体,在所受合力突然消失,或者不足以提供圆周运动所需的向心力时,做逐渐远离圆心的运动,这种运动叫做离心运动.
2、条件:
0 ≤F合<mω2r
供<需
物体沿切线方向飞出远离圆心
物体做匀速圆周运动
物体做逐渐远离圆心的运动
离心抛掷
离心脱水
离心分离
离心甩干
3、离心现象的应用:
4、离心运动的防止
O
F静
v
在水平公路上行驶的汽车,转弯时所需的向心力是由车轮与路面的静摩擦力提供的。如果转弯时速度过大,所需向心力大于最大静摩擦力(不足以提供向心力),汽车将做离心运动而造成交通事故.因此,在公路弯道处,车辆行驶不允许超过规定的速度.
当 时,汽车做离心运动
高速转动的砂轮、飞轮等,都不得超过允许的最大转速。转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力,离心运动会使它们破裂,酿成事故.
O
F
v
本课小结
1.如图所示,光滑的水平面上,小球m在拉力F作用下做匀速圆周运动,若小球到达P点时F突然发生变化,下列关于小球运动的说法正确的是( )
A.F突然消失,小球将沿轨迹Pa做离心运动
B.F突然变小,小球将沿轨迹Pa做离心运动
C.F突然变大,小球将沿轨迹Pb做离心运动
D.F突然变小,小球将沿轨迹Pc逐渐靠近圆心
解析:若F突然消失,小球所受合力突变为0,将沿切线方向匀速飞出,选项A正确。若F突然变小,不足以提供所需向心力,小球将做逐渐远离圆心的离心运动,选项B、D错误。若F突然变大,超过了所需向心力,小球将做逐渐靠近圆心的近心运动,选项C错误。
当堂检测
A
2.铁路转弯处的圆弧半径为R,内侧和外侧的高度差为h,L为两轨间的距离,且L>h。如果列车转弯速率大于 ,则( )
A.外侧铁轨与轮缘间产生挤压
B.铁轨与轮缘间无挤压
C.内侧铁轨与轮缘间产生挤压
D.内外侧铁轨与轮缘间均有挤压
A
3.一辆运输西瓜的小汽车(可视为质点),以大小为v的速度经过一座半径为R的拱形桥。在桥的最高点,其中一个质量为m的西瓜A(位置如图所示)受到周围的西瓜对它的作用力的大小为( )
C
4.如图所示,高速公路转弯处弯道圆半径R=250 m,汽车轮胎与路面间的动摩擦因数μ=0.25。若路面是水平的,问汽车转弯时不发生侧向滑动(离心现象)所许可的最大速率vm为多大 当超过vm时,将会出现什么现象 (g取10 m/s2)
答案:90 km/h 汽车做离心运动或出现翻车
第
节
3
离心现象
高中物理 必修第二册
第3章
1.学会通过车辆转弯问题及凹、凸桥和过山车问题分析水平面内和竖直面内的圆周运动。
2.知道什么是离心运动,学会通过实例分析离心运动。
3.学会运用圆周运动知识分析生活中的实际问题。
学习目标
思考:为什么在拐弯处容易发生事故?
应该如何避免这种事件的发生?
引入
汽车在水平地面上转弯时是什么力提供向心力的呢
O
mg
N
f
一、车辆转弯时所需的向心力
汽车在水平路面上转弯所需要的向心力来源:
当汽车转弯的半径一定时,汽车的速度v越大,所需的向心力也越大,静摩擦力也越大,汽车做圆周运动。
供=需
匀速圆周运动
供<需
侧滑
当所需要的向心力大于所提供的向心力(即最大静摩擦力)时,汽车将发生侧滑现象。
O
mg
N
f
赛道的设计
思考:火车转弯时是在做圆周运动,什么力提供向心力?
G
外轨
内轨
N
F
外轨对轮缘的弹力
内外轨道一样高
O
火车水平转弯时情况分析:由外侧轨道对车轮轮缘的挤压力提供向心力
思考:靠这种办法得到的向心力缺点是什么?如何解决这一实际问题?
外轨高于内轨
在转弯处外轨略高于内轨
θ
N
G
O
F合
θ
火车转弯所需的向心力的方向是在水平方向上还是在与斜面平行的方向上?
轨道对轮缘无挤压,此时火车的速度为多大?
θ很小时,sinθ≈tanθ
若火车的速度大于或小于这个值时,轨道对轮缘有挤压吗?
2、当
1、当 :
G
N
θ
轮缘受到外轨向内的挤压力,外轨易损坏。
G
N
θ
F
F
轮缘受到内轨向外的挤压力,内轨易损坏。
思考:为什么桥的外形都是凸起的而没有凹陷的?
这样的设计跟向心力又有怎么样的关系呢?
二、竖直平面内的圆周运动分析
1.求汽车以速度过半径为 的拱桥最高点时对拱桥的压力?
【解】和的合力提供汽车做圆周运动的向心力,由牛顿第二定律得:
可见汽车的速度越大对桥的压力越小。
当 时汽车对桥的压力为零。(临界速度)
思考:当 大于时,汽车做什么运动?
汽车脱离桥面,做平抛运动。
N<mg,失重状态
2.求汽车过凹形路段最低点时对路面的压力?
【解】和的合力提供汽车做圆周运动的向心力,由牛顿第二定律得:
可见汽车的速度v越大,对桥的压力越大。
超重状态
若汽车通过凹桥的速度增大,会出现什么情况?
思考:过山车为什么在最高点也不会掉下来
讨论
物做近心运动
① 绳和内轨模型
理论研究
mg
N
v
轨道提供支持力,绳子提供拉力。
v
② 杆儿和双轨模型
能过最高点的临界条件:
当速度 > 时, 杆对小球是拉力;
当速度 < 时, 杆对小球是支持力;
当速度 = 时, 杆对小球无作用力。
mg
N
杆既可以提供拉力,也可以提供支持力。
N
当
向心力的“供求”关系——所需向心力与提供向心力;
思考:如果所需向心力与提供向心力大小不相等时物体将如何运动?
F合 = mω2r,
O
物体做匀速圆周运动
供=需
三、生活中的离心运动
O
F合 = mω2r,
F合<mω2r ,
F 合= 0 ,
1、定义:做匀速圆周运动的物体,在所受合力突然消失,或者不足以提供圆周运动所需的向心力时,做逐渐远离圆心的运动,这种运动叫做离心运动.
2、条件:
0 ≤F合<mω2r
供<需
物体沿切线方向飞出远离圆心
物体做匀速圆周运动
物体做逐渐远离圆心的运动
离心抛掷
离心脱水
离心分离
离心甩干
3、离心现象的应用:
4、离心运动的防止
O
F静
v
在水平公路上行驶的汽车,转弯时所需的向心力是由车轮与路面的静摩擦力提供的。如果转弯时速度过大,所需向心力大于最大静摩擦力(不足以提供向心力),汽车将做离心运动而造成交通事故.因此,在公路弯道处,车辆行驶不允许超过规定的速度.
当 时,汽车做离心运动
高速转动的砂轮、飞轮等,都不得超过允许的最大转速。转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力,离心运动会使它们破裂,酿成事故.
O
F
v
本课小结
1.如图所示,光滑的水平面上,小球m在拉力F作用下做匀速圆周运动,若小球到达P点时F突然发生变化,下列关于小球运动的说法正确的是( )
A.F突然消失,小球将沿轨迹Pa做离心运动
B.F突然变小,小球将沿轨迹Pa做离心运动
C.F突然变大,小球将沿轨迹Pb做离心运动
D.F突然变小,小球将沿轨迹Pc逐渐靠近圆心
解析:若F突然消失,小球所受合力突变为0,将沿切线方向匀速飞出,选项A正确。若F突然变小,不足以提供所需向心力,小球将做逐渐远离圆心的离心运动,选项B、D错误。若F突然变大,超过了所需向心力,小球将做逐渐靠近圆心的近心运动,选项C错误。
当堂检测
A
2.铁路转弯处的圆弧半径为R,内侧和外侧的高度差为h,L为两轨间的距离,且L>h。如果列车转弯速率大于 ,则( )
A.外侧铁轨与轮缘间产生挤压
B.铁轨与轮缘间无挤压
C.内侧铁轨与轮缘间产生挤压
D.内外侧铁轨与轮缘间均有挤压
A
3.一辆运输西瓜的小汽车(可视为质点),以大小为v的速度经过一座半径为R的拱形桥。在桥的最高点,其中一个质量为m的西瓜A(位置如图所示)受到周围的西瓜对它的作用力的大小为( )
C
4.如图所示,高速公路转弯处弯道圆半径R=250 m,汽车轮胎与路面间的动摩擦因数μ=0.25。若路面是水平的,问汽车转弯时不发生侧向滑动(离心现象)所许可的最大速率vm为多大 当超过vm时,将会出现什么现象 (g取10 m/s2)
答案:90 km/h 汽车做离心运动或出现翻车
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
