3.1.1 椭圆及其标准方程 第一课时 课件(共33张PPT)
文档属性
| 名称 | 3.1.1 椭圆及其标准方程 第一课时 课件(共33张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 17.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-29 21:09:29 | ||
图片预览




文档简介
(共33张PPT)
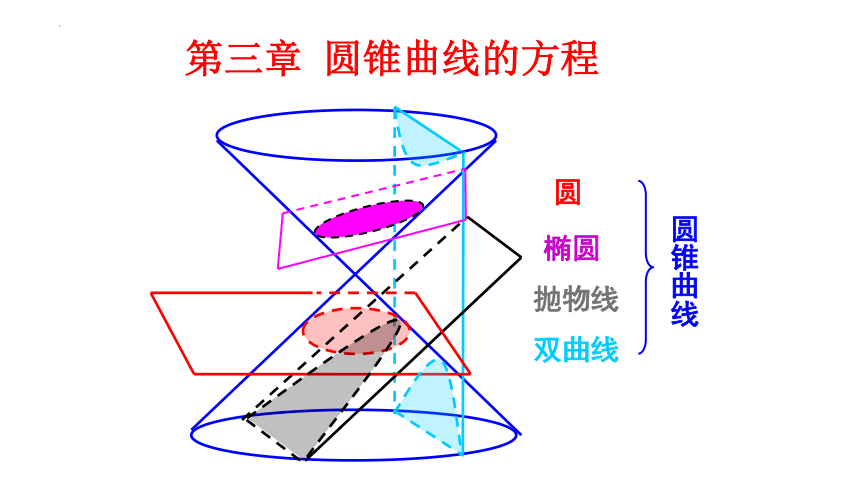
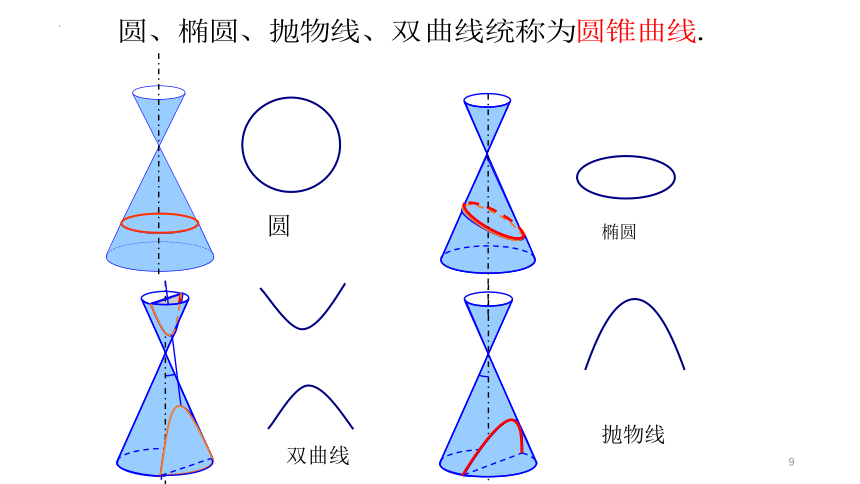
圆
椭圆
抛物线
双曲线
圆锥曲线
第三章 圆锥曲线的方程
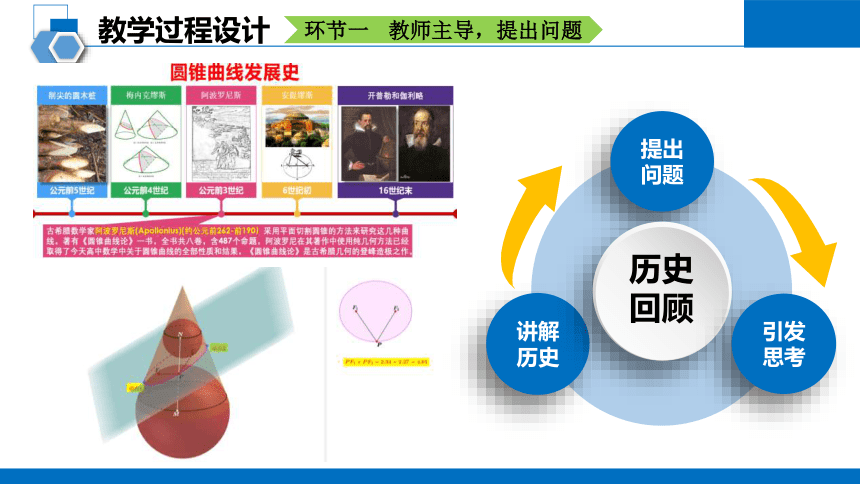
教学过程设计
环节一 教师主导,提出问题
讲解历史
提出问题
历史
回顾
引发思考
圆锥曲线的由来及无处不在的椭圆
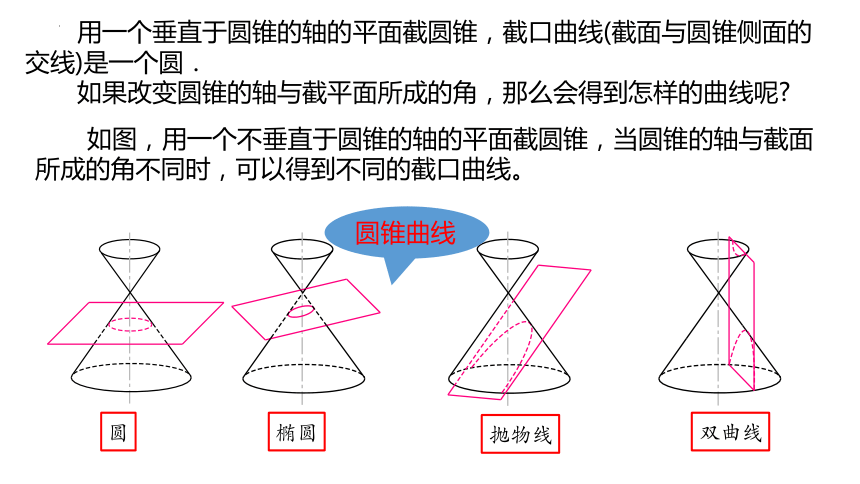
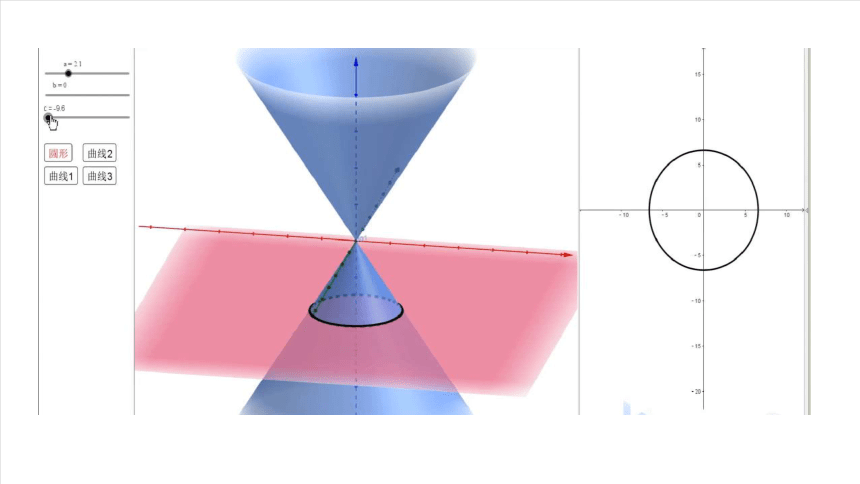
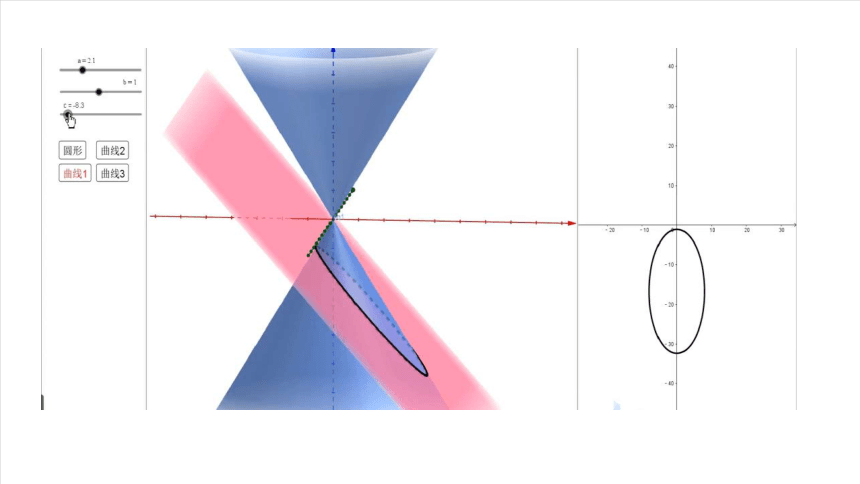
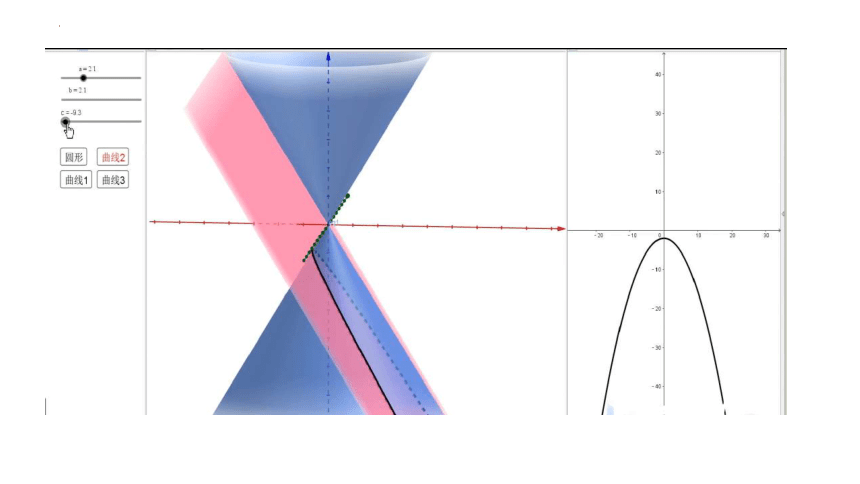
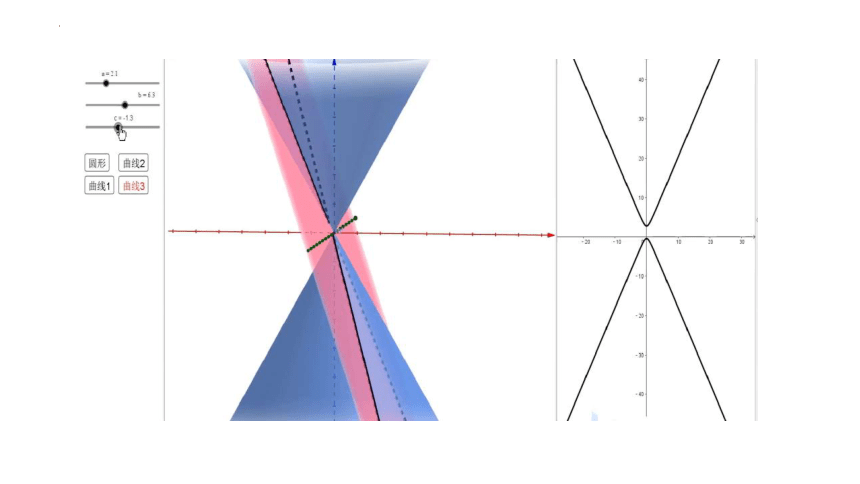
用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.
如果改变圆锥的轴与截平面所成的角,那么会得到怎样的曲线呢
如图,用一个不垂直于圆锥的轴的平面截圆锥,当圆锥的轴与截面所成的角不同时,可以得到不同的截口曲线。
椭圆
抛物线
双曲线
圆
圆锥曲线
动手操作
动手操作
双曲线抛物线圆椭圆
圆锥的应用
0
圆锥曲线在生产生活中应用广泛。比如天宫一号的运行轨迹是椭圆,中国“天眼”外形轴截面是抛物线。笛卡尔发明坐标系后,人们就开始借助坐标系,运用代数方法研究圆锥曲线。本章我们继续用坐标法来研究圆锥曲线的几何特征,揭示它的神奇与奥秘。
开普勒(德国)
1571——1630
开普勒第一定律:
所有行星围绕太阳运动的轨道都是椭圆
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类生活中具有广泛的应用,那么,椭圆到底有怎样的几何特征 我们该如何利用这些特征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础
几何特征 代数方程
直线
定点、定方向
圆
定点、定长
坐标法
复习旧知
01
《直线与圆的方程》中我们学习了:
k存在时
教学过程设计
环节二 学生探求,发现问题
动手操作
发现问题
数学
实验
完善定义
动手实验,认识椭圆
02
01
实验:取一条定长的细绳,若把细绳两端都固定在图板的同一点,套上铅笔,拉紧绳子,移动笔尖,这时笔尖画出来的轨迹是一个圆,如果把细绳的两端点拉开一段距离,分别固定在图板的两点F1、F2(定点),套上铅笔,拉紧绳子,移动笔尖(动点),画出的轨迹是什么曲线?
问题:怎样画出椭圆?
动手实验,认识椭圆
02
壹
“操作过程中套上铅笔,拉紧绳子”意味着什么?
贰
笔尖移动过程中满足的几何条件是什么?
叁
画出来的这样的图象有什么共同特点?
在这一过程中, 移动的笔尖(动点)满足的几何条件是什么
动画演示
在这一过程中, 移动的笔尖(动点)满足的几何条件是:
移动的笔尖M(动点)到固定在图板上的两定点F1, F2的距离之和是定值, 并且这个定值大于两定点间的距离,即
图钉不动
两个定点
笔尖滑动
一个动点
绳长不变
距离之和不变
平面内与两个定点F1, F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫椭圆. 这两个定点F1, F2叫做椭圆的焦点,两焦点之间的距离| F1F2|叫做椭圆的焦距.
1. 椭圆的定义:
思考 动点的轨迹是椭圆应满足什么条件?
① 在平面内----(这是前提条件);
② 动点M到两个定点F1, F2的距离之和是常数;
动点M的轨迹是线段F1F2 ;
动点M没有轨迹 .
F1
F2
M
③
求椭圆的方程
如何建立平面直角坐标系可能使得椭圆方程方程简单
原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)
(对称、“简洁”)
.
.
O
x
y
.
.
O
x
y
O
x
y
O
x
y
03
取过焦点的直线为x轴,线段的垂直平分线为y轴,建立平面直角坐标系(如图).
由椭圆的定义得,限制条件:
建
设
设M(x,y)是椭圆上任意一点,椭圆的焦距2c(c>0),M与 F1和F2 的距离的和等于正常数2a(2a>2c),则 F1、F2 的坐标分别是(-c,0)、(c,0)
因为
所以
求椭圆的方程
03
限
代
化
1
2
y
O
F
F
M
x
几何条件代数化
(x,y)
方法一:移项平方法
移项,再平方
两边再平方,得
整理得
两边除以a2(a2-c2)得
求椭圆的方程
03
(1)
等价变形
方法二:平方差法
所以
所以
上式平方再化简得
因为
求椭圆的方程
03
(1)
1
2
y
O
F
F
M
x
代数式的几何意义
问题:观察右图,你能从中找出表示 的线段吗?
令 ,则(2)式可化为:
O
x
y
F1
F2
P
求椭圆的方程
03
(1)
a
b
c
代数量a,b,c的几何意义:直角三角形OPF2三边长。满足c2=a2-b2
从上述过程可以看到,椭圆上任一点的坐标都满足方程(2)
方程(2)的解对应坐标的点都在椭圆上。
则方程(2)为椭圆的标准方程。
求椭圆的方程
03
1
2
y
O
F
F
M
x
F1
F2
P
x
y
O
c
a
b
思考1 观察图, 你能从中找出表示a,b,c的线段吗?
它所表示的椭圆的焦点在x轴上,焦点是F1(-c,0), F2(c,0),
中心在坐标原点的椭圆方程 ,其中c2=a2-b2 .
如果椭圆的焦点在y轴上,那么椭圆的标准方程又是怎样的呢
02
03
01
也是椭圆的标准方程.
求椭圆的方程
03
1
O
F
y
x
2
F
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;
方程的左边是平方和,右边是 1 .
不同点:焦点在 x 轴的椭圆 x2 项分母较大.
焦点在 y 轴的椭圆 y2 项分母较大.
图 形
方 程
焦 点
F1(-c,0) F2(c,0)
F1(0,-c) F2(0,c)
a,b,c之间的关系
|MF1|+|MF2|=2a>2c=|F1F2| (2a>2c>0)
定 义
1
2
y
O
F
F
M
x
1
O
F
y
x
2
F
M
知识小结
04
例题讲解
05
例1 已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点 ,求它的标准方程。
条件 几何角度 代数角度
椭圆
需要两个定点且距离和为定值
有标准方程但方程形式不唯一
两个焦点坐标 分别是(-2,0),(2,0)
给出重要几何量两个定点
1.给出参数c的值
2.确定方程形式
可以确定距离和
分析:
几何角度
代数角度
定义法
待定系数法
例题讲解
05
例1 已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点 ,求它的标准方程。
(法1)
例题讲解:求椭圆的标准方程
(法2)
求a,b
定型
定量
焦点位置
未知焦点位置:巧设方程
14
【方法说明】
(3) 求椭圆的标准方程,要先定“位”,
1. 求椭圆标准方程的主要方法有:
a, b, c 满足的关系有:
根据焦点位置设方程,代入计算出待定字母的值.
用定义寻找a, b, c的方程;
(1) 定义法:
(2) 待定系数法:
待定系数法更为常用,是解此类问题的通法.
即求 a, b 的大小 .
即确定焦点的位置;
其次是定“量”,
圆
椭圆
抛物线
双曲线
圆锥曲线
第三章 圆锥曲线的方程
教学过程设计
环节一 教师主导,提出问题
讲解历史
提出问题
历史
回顾
引发思考
圆锥曲线的由来及无处不在的椭圆
用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.
如果改变圆锥的轴与截平面所成的角,那么会得到怎样的曲线呢
如图,用一个不垂直于圆锥的轴的平面截圆锥,当圆锥的轴与截面所成的角不同时,可以得到不同的截口曲线。
椭圆
抛物线
双曲线
圆
圆锥曲线
动手操作
动手操作
双曲线抛物线圆椭圆
圆锥的应用
0
圆锥曲线在生产生活中应用广泛。比如天宫一号的运行轨迹是椭圆,中国“天眼”外形轴截面是抛物线。笛卡尔发明坐标系后,人们就开始借助坐标系,运用代数方法研究圆锥曲线。本章我们继续用坐标法来研究圆锥曲线的几何特征,揭示它的神奇与奥秘。
开普勒(德国)
1571——1630
开普勒第一定律:
所有行星围绕太阳运动的轨道都是椭圆
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类生活中具有广泛的应用,那么,椭圆到底有怎样的几何特征 我们该如何利用这些特征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础
几何特征 代数方程
直线
定点、定方向
圆
定点、定长
坐标法
复习旧知
01
《直线与圆的方程》中我们学习了:
k存在时
教学过程设计
环节二 学生探求,发现问题
动手操作
发现问题
数学
实验
完善定义
动手实验,认识椭圆
02
01
实验:取一条定长的细绳,若把细绳两端都固定在图板的同一点,套上铅笔,拉紧绳子,移动笔尖,这时笔尖画出来的轨迹是一个圆,如果把细绳的两端点拉开一段距离,分别固定在图板的两点F1、F2(定点),套上铅笔,拉紧绳子,移动笔尖(动点),画出的轨迹是什么曲线?
问题:怎样画出椭圆?
动手实验,认识椭圆
02
壹
“操作过程中套上铅笔,拉紧绳子”意味着什么?
贰
笔尖移动过程中满足的几何条件是什么?
叁
画出来的这样的图象有什么共同特点?
在这一过程中, 移动的笔尖(动点)满足的几何条件是什么
动画演示
在这一过程中, 移动的笔尖(动点)满足的几何条件是:
移动的笔尖M(动点)到固定在图板上的两定点F1, F2的距离之和是定值, 并且这个定值大于两定点间的距离,即
图钉不动
两个定点
笔尖滑动
一个动点
绳长不变
距离之和不变
平面内与两个定点F1, F2的距离的和等于常数(大于|F1F2 |)的点的轨迹叫椭圆. 这两个定点F1, F2叫做椭圆的焦点,两焦点之间的距离| F1F2|叫做椭圆的焦距.
1. 椭圆的定义:
思考 动点的轨迹是椭圆应满足什么条件?
① 在平面内----(这是前提条件);
② 动点M到两个定点F1, F2的距离之和是常数;
动点M的轨迹是线段F1F2 ;
动点M没有轨迹 .
F1
F2
M
③
求椭圆的方程
如何建立平面直角坐标系可能使得椭圆方程方程简单
原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)
(对称、“简洁”)
.
.
O
x
y
.
.
O
x
y
O
x
y
O
x
y
03
取过焦点的直线为x轴,线段的垂直平分线为y轴,建立平面直角坐标系(如图).
由椭圆的定义得,限制条件:
建
设
设M(x,y)是椭圆上任意一点,椭圆的焦距2c(c>0),M与 F1和F2 的距离的和等于正常数2a(2a>2c),则 F1、F2 的坐标分别是(-c,0)、(c,0)
因为
所以
求椭圆的方程
03
限
代
化
1
2
y
O
F
F
M
x
几何条件代数化
(x,y)
方法一:移项平方法
移项,再平方
两边再平方,得
整理得
两边除以a2(a2-c2)得
求椭圆的方程
03
(1)
等价变形
方法二:平方差法
所以
所以
上式平方再化简得
因为
求椭圆的方程
03
(1)
1
2
y
O
F
F
M
x
代数式的几何意义
问题:观察右图,你能从中找出表示 的线段吗?
令 ,则(2)式可化为:
O
x
y
F1
F2
P
求椭圆的方程
03
(1)
a
b
c
代数量a,b,c的几何意义:直角三角形OPF2三边长。满足c2=a2-b2
从上述过程可以看到,椭圆上任一点的坐标都满足方程(2)
方程(2)的解对应坐标的点都在椭圆上。
则方程(2)为椭圆的标准方程。
求椭圆的方程
03
1
2
y
O
F
F
M
x
F1
F2
P
x
y
O
c
a
b
思考1 观察图, 你能从中找出表示a,b,c的线段吗?
它所表示的椭圆的焦点在x轴上,焦点是F1(-c,0), F2(c,0),
中心在坐标原点的椭圆方程 ,其中c2=a2-b2 .
如果椭圆的焦点在y轴上,那么椭圆的标准方程又是怎样的呢
02
03
01
也是椭圆的标准方程.
求椭圆的方程
03
1
O
F
y
x
2
F
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;
方程的左边是平方和,右边是 1 .
不同点:焦点在 x 轴的椭圆 x2 项分母较大.
焦点在 y 轴的椭圆 y2 项分母较大.
图 形
方 程
焦 点
F1(-c,0) F2(c,0)
F1(0,-c) F2(0,c)
a,b,c之间的关系
|MF1|+|MF2|=2a>2c=|F1F2| (2a>2c>0)
定 义
1
2
y
O
F
F
M
x
1
O
F
y
x
2
F
M
知识小结
04
例题讲解
05
例1 已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点 ,求它的标准方程。
条件 几何角度 代数角度
椭圆
需要两个定点且距离和为定值
有标准方程但方程形式不唯一
两个焦点坐标 分别是(-2,0),(2,0)
给出重要几何量两个定点
1.给出参数c的值
2.确定方程形式
可以确定距离和
分析:
几何角度
代数角度
定义法
待定系数法
例题讲解
05
例1 已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点 ,求它的标准方程。
(法1)
例题讲解:求椭圆的标准方程
(法2)
求a,b
定型
定量
焦点位置
未知焦点位置:巧设方程
14
【方法说明】
(3) 求椭圆的标准方程,要先定“位”,
1. 求椭圆标准方程的主要方法有:
a, b, c 满足的关系有:
根据焦点位置设方程,代入计算出待定字母的值.
用定义寻找a, b, c的方程;
(1) 定义法:
(2) 待定系数法:
待定系数法更为常用,是解此类问题的通法.
即求 a, b 的大小 .
即确定焦点的位置;
其次是定“量”,
