5.6 应用一元一次方程-追赶小明 课件(共28张PPT)-2023-2024学年七年级数学上册同步精品课件(北师大版)
文档属性
| 名称 | 5.6 应用一元一次方程-追赶小明 课件(共28张PPT)-2023-2024学年七年级数学上册同步精品课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览







文档简介
北师大版 数学 七年级上册
6 应用一元一次方程----追赶小明
第五章 一元一次方程
学习目标
1.借助“线段图”分析复杂问题中的数量关系,从而建立方程解决实际问题.(重点)
2.发展分析问题,解决问题的能力,进一步体会方程模型的作用.(难点)
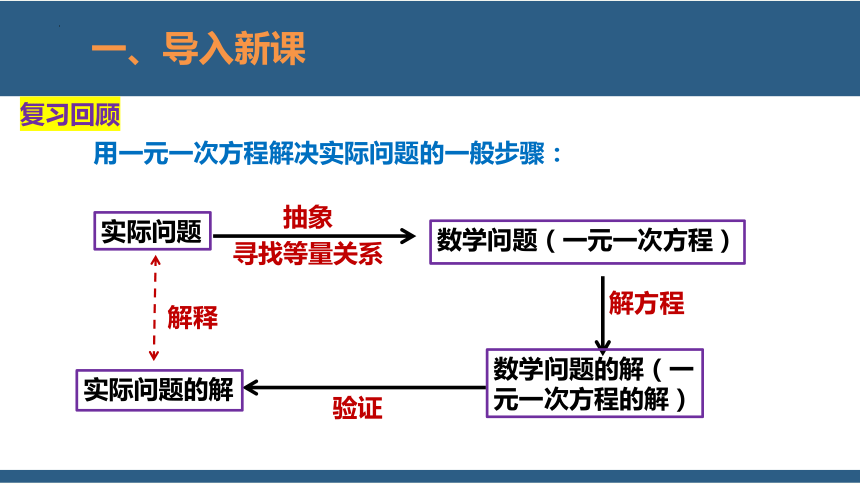
一、导入新课
复习回顾
用一元一次方程解决实际问题的一般步骤:
实际问题
抽象
寻找等量关系
数学问题(一元一次方程)
解方程
数学问题的解(一
元一次方程的解)
验证
实际问题的解
解释
一、导入新课
情境导入
小明每天早上要在7:50分之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180米/分的速度去追小明.
爸爸能不能在小明到达学校之前追上他呢?
二、新知探究
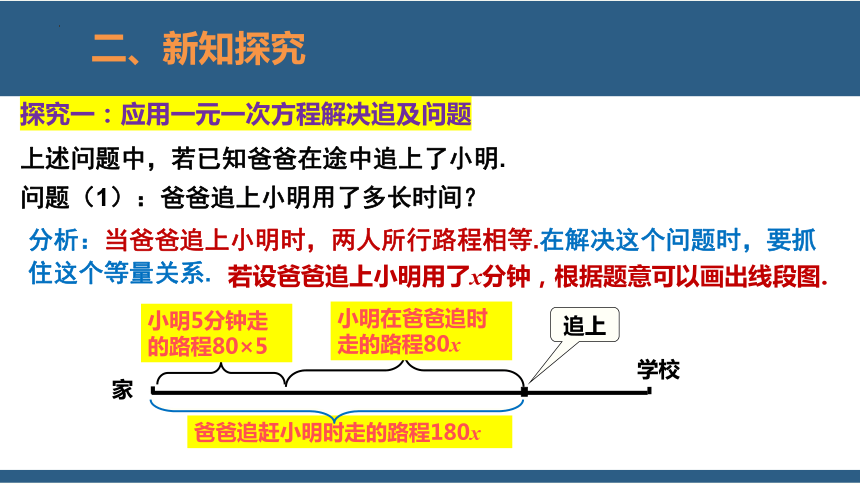
探究一:应用一元一次方程解决追及问题
上述问题中,若已知爸爸在途中追上了小明.
问题(1):爸爸追上小明用了多长时间?
分析:当爸爸追上小明时,两人所行路程相等.在解决这个问题时,要抓住这个等量关系.
家
学校
追上
小明5分钟走的路程80×5
小明在爸爸追时走的路程80x
爸爸追赶小明时走的路程180x
若设爸爸追上小明用了x分钟,根据题意可以画出线段图.
问题(2)追上小明时,距离学校还有多远?
家
学校
追上
小明5分钟走的路程80×5
小明在爸爸追时走的路程80x
爸爸追赶小明时走的路程180x
二、新知探究
解:(1)设爸爸追上小明用了x分钟.
根据题意,得 180x=5×80+80x
化简,得 100x=400
x=4
因此,爸爸追上小明用了4分钟.
?
1000-720=280(米)
所以,追上小明时,距离学校还有280米。
(2)180×4=720(米)
二、新知探究
问题1:后队追上前队用了多长时间 ?
问题2:后队追上前队时联络员行了多少路程?
问题3:联络员第一次追上前队时用了多长时间?
议一议:育红学校七年级学生步行到郊外旅行:(1)班的学生组成前队,步行速度为4km/h,(2)班的学生组成后队,速度为6km/h。前队出发1h后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h。
根据上面的事实提出问题并尝试去解答.
二、新知探究
问题1:后队追上前队用了多长时间 ?
解:设后队追上前队用了x小时,
由题意,得 6x = 4x + 4
解方程,得 x =2
答:后队追上前队时用了2小时。
问题2:后队追上前队时联络员行了多少路程?
解:由问题1得后队追上前队用了2小时,因此,联络员共行进了
12 × 2 = 24 (千米)
答:后队追上前队时联络员行了24千米。
二、新知探究
问题3:联络员第一次追上前队时用了多长时间?
解:设联络员第一次追上前队时用了x小时,
由题意得: 12x = 4x + 4
解方程得:x =0.5
答:联络员第一次追上前队时用了0.5小时。
二、新知探究
知识归纳
甲、乙两人同向出发,甲追乙这类问题为追及问题:
对于行程问题,通常借助“线段图”来分析问题中的数量关系.
(1)对于同向同时不同地的问题,如图所示,甲的行程-乙的行程=两出发地的距离;
注意:同向而行注意始发时间和地点.
(2)对于同向同地不同时的问题,如图所示,甲的行程=乙先走的路程+乙后走的路程.
线段图:
甲
乙
二、新知探究
甲、乙两站间的路程为 450 千米,一列慢车从甲站开出,每小时行驶 65 千米,一列快车从乙站开出,每小时行驶 85 千米.
(1)两车同时开出,相向而行,经过多少小时相遇?
解:(1)设 两车行驶了xh相遇,
根据题意得 65x+85x=450,
解,得 x = 3.
答:两车经过3h相遇.
分析:等量关系:慢车路程+快车路程=甲乙之间的距离.
探究二:应用一元一次方程解决相遇问题
相遇
慢车行驶的路程65x
甲乙两地之间的距离450km
快车行驶的路程85x
甲
乙
线段图:
二、新知探究
(2)快车先开30min,两车相向而行,慢车行驶了多少小时两车相遇?
相遇
快车先开30min行驶的路程85×0.5
慢车行驶的路程65y
甲乙两地之间的距离450km
快车在慢车走时行驶的路程85y
解:(2)设慢车行驶了y小时两车相遇.
据题意得 65y+85(y+0.5)=450,
解,得 y= ??????????????????.
答:慢车行驶了??????????????????小时两车相遇.
?
相遇问题:
关于两人从两地出发相向而行的行程问题称为相遇问题,这类问题往往根据路程之和等于总路程列方程.
如图所示,甲的行程+乙的行程=两地相距的路程.
二、新知探究
知识归纳
二、新知探究
思考:操场一周是400米,小明每秒跑5米,小强每秒跑4米,两人绕跑道同时同地同向而行,他俩能相遇吗?
小强
小明
同时同地
同向而行
能相遇
探究三:环形跑道中的追及和相遇问题
分 析:
二、新知探究
操场一周是400米,小明每秒跑5米,小强骑自行车每秒15米.
(1)两人绕跑道同时同地同向而行,经过几秒钟两人第一次相遇?
(2)两人同时同地相背而行,则两个人何时相遇?
解:设经过x秒两人第一次相遇,
根据题意,得15x-5x=400,
解得 x=40.
答:经过40秒两人第一次相遇.
(2)设经过x秒两人第一次相遇,
根据题意,得 15x+5x=400,
解得 x=20 .
答:经过 20 秒两人第一次相遇.
跟踪练习
二、新知探究
环形跑道长s米,设v甲>v乙,经过t秒甲、乙第一次相遇.
一般有如下两种情形:
①同时同地、同向而行:
v甲t-v乙t=s.
②同时同地、背向而行:
v甲t+v乙t=s.
环形跑道问题
追及问题
相遇问题
知识归纳
解:设甲、乙两地距离是x千米,
由题意得 ????????????+??????????????????????=????????,
解得 x=286,
答:甲、乙两地的距离是286千米.
?
二、新知探究
分析:本题涉及水流速度:
顺水速度=船速+水速;逆水速度=船速-水速.
已知船在静水中的速度是24千米/时,水流速度是2千米/时,该船在甲、乙两地间行驶一个来回共用了24小时,求甲、乙两地的距离是多少?
做一做
1.顺(逆)水问题中的有关公式:
①顺水速度=静水中的速度+水流速度;
②逆水速度=静水中的速度-水流速度;
③顺水速度-逆水速度=2×水流速度.
2.顺(逆)风问题中的有关公式:
①顺风速度=无风速度+风速;
②逆风速度=无风速度-风速;
③顺风速度-逆风速度=2×风速.
二、新知探究
知识归纳
三、典例精析
例1:小明家离学校2.9千米.一天,小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,则小明爸爸从家出发几分钟后接到小明?
[解析] 设小明爸爸出发x分钟后接到小明.
可以画出线段图如右图所示.
解:设小明爸爸从家出发x分钟后接到小明,
由题意,得200x+60(x+5)=2900.
解这个方程,得x=10.
因此,小明爸爸从家出发10分钟后接到小明.
三、典例精析
例2:小明的爷爷每天都步行到距离家3.2千米的公园去打太极拳.周日早晨,爷爷出发半小时后,小明发现爷爷忘记带家门钥匙了,小明就骑自行车去给爷爷送钥匙.如果爷爷的速度是4千米/时,小明骑自行车的速度是12千米/时,当小明追上爷爷时,爷爷到公园了吗?
解:设小明用x小时追上爷爷.
因为3千米<3.2千米.
所以小明追上爷爷时,爷爷没有到公园.
三、典例精析
例3:一架飞机在两个城市之间飞行,当顺风飞行时需2.9 h,当逆风飞行时则需3.1 h.已知风速为20 km/h,求无风时飞机的航速和这两个城市之间的距离.
解:设无风时飞机的航速为x km/h,
根据题意,得 2.9(x+20)=3.1(x-20).
解这个方程,得 x=600.
则3.1(x-20)=1798.
因此,无风时飞机的航速为600 km/h,这两个城市之间的距离为1798 km.
2.小明骑自行车到学校上学,若每小时骑15千米,可早到10分钟,若每小时骑13千米,则迟到5分钟,设他家到学校的路程为x千米,下列方程正确的是( )
四、当堂练习
1.小明和小刚从相距25.2千米的两地同时相向而行,小明每小时走4千米,3小时后两人相遇,设小刚的速度为x千米/时,列方程得( )
A.4+3x=25.2 B.3×4+x=25.2
C.3(4+x)=25.2 D.3(x-4)=25.2
C
A
四、当堂练习
3.甲、乙两人在环形跑道上练习跑步,已知环形跑道一圈长400米,乙每秒跑6米,甲每秒跑8米.如果甲在乙前面8米处同时同向出发,那么经过几秒两人首次相遇( )
A.208秒 B.204秒 C.200秒 D.196秒
D
4.一列长30米的队伍以每分钟60米的速度向前行进,队尾一名同学用1分钟从队尾走到队头,这位同学走的路程为____米,速度是____米/分.
90
90
四、当堂练习
5.甲、乙两人赛跑,甲的速度是8米/秒,乙的速度是5米/秒,如果甲从起点处往后退20米,乙从起点处向前进10米,若甲、乙两人同时出发,则甲经过几秒钟追上乙?
解:设甲经过x秒追上乙.
由题意,得8x-5x=20+10.
解这个方程,得x=10.
因此,甲经过10秒追上乙.
四、当堂练习
6.A,B两地相距30千米.甲、乙两人分别从A,B两地同时出发,相向而行.已知甲比乙每小时多走1千米,经过2.5小时两人相遇,求甲、乙两人的速度.
解:设乙的速度为x千米/时,则甲的速度为(x+1)千米/时.
根据题意,得2.5x+2.5(x+1)=30.
解这个方程,得x=5.5.则x+1=6.5.
因此,甲、乙两人的速度分别为6.5千米/时、5.5千米/时.
四、当堂练习
7.一架飞机在两城市之间飞行,风速为24千米/时,顺风飞行需要2小时50分,逆风飞行需要3小时.求无风时飞机的飞行速度和两城之间的航程.
五、课堂小结
同向追
及问题
相向相
遇问题
应用一元一次方程
——追赶小明
同地不同时:甲路程=乙路程
同时不同地:甲路程+路程差=乙路程
甲的路程+乙的路程=总路程
六、作业布置
习题5.9
6 应用一元一次方程----追赶小明
第五章 一元一次方程
学习目标
1.借助“线段图”分析复杂问题中的数量关系,从而建立方程解决实际问题.(重点)
2.发展分析问题,解决问题的能力,进一步体会方程模型的作用.(难点)
一、导入新课
复习回顾
用一元一次方程解决实际问题的一般步骤:
实际问题
抽象
寻找等量关系
数学问题(一元一次方程)
解方程
数学问题的解(一
元一次方程的解)
验证
实际问题的解
解释
一、导入新课
情境导入
小明每天早上要在7:50分之前赶到距家1000米的学校上学.一天,小明以80米/分的速度出发,5分钟后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180米/分的速度去追小明.
爸爸能不能在小明到达学校之前追上他呢?
二、新知探究
探究一:应用一元一次方程解决追及问题
上述问题中,若已知爸爸在途中追上了小明.
问题(1):爸爸追上小明用了多长时间?
分析:当爸爸追上小明时,两人所行路程相等.在解决这个问题时,要抓住这个等量关系.
家
学校
追上
小明5分钟走的路程80×5
小明在爸爸追时走的路程80x
爸爸追赶小明时走的路程180x
若设爸爸追上小明用了x分钟,根据题意可以画出线段图.
问题(2)追上小明时,距离学校还有多远?
家
学校
追上
小明5分钟走的路程80×5
小明在爸爸追时走的路程80x
爸爸追赶小明时走的路程180x
二、新知探究
解:(1)设爸爸追上小明用了x分钟.
根据题意,得 180x=5×80+80x
化简,得 100x=400
x=4
因此,爸爸追上小明用了4分钟.
?
1000-720=280(米)
所以,追上小明时,距离学校还有280米。
(2)180×4=720(米)
二、新知探究
问题1:后队追上前队用了多长时间 ?
问题2:后队追上前队时联络员行了多少路程?
问题3:联络员第一次追上前队时用了多长时间?
议一议:育红学校七年级学生步行到郊外旅行:(1)班的学生组成前队,步行速度为4km/h,(2)班的学生组成后队,速度为6km/h。前队出发1h后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12km/h。
根据上面的事实提出问题并尝试去解答.
二、新知探究
问题1:后队追上前队用了多长时间 ?
解:设后队追上前队用了x小时,
由题意,得 6x = 4x + 4
解方程,得 x =2
答:后队追上前队时用了2小时。
问题2:后队追上前队时联络员行了多少路程?
解:由问题1得后队追上前队用了2小时,因此,联络员共行进了
12 × 2 = 24 (千米)
答:后队追上前队时联络员行了24千米。
二、新知探究
问题3:联络员第一次追上前队时用了多长时间?
解:设联络员第一次追上前队时用了x小时,
由题意得: 12x = 4x + 4
解方程得:x =0.5
答:联络员第一次追上前队时用了0.5小时。
二、新知探究
知识归纳
甲、乙两人同向出发,甲追乙这类问题为追及问题:
对于行程问题,通常借助“线段图”来分析问题中的数量关系.
(1)对于同向同时不同地的问题,如图所示,甲的行程-乙的行程=两出发地的距离;
注意:同向而行注意始发时间和地点.
(2)对于同向同地不同时的问题,如图所示,甲的行程=乙先走的路程+乙后走的路程.
线段图:
甲
乙
二、新知探究
甲、乙两站间的路程为 450 千米,一列慢车从甲站开出,每小时行驶 65 千米,一列快车从乙站开出,每小时行驶 85 千米.
(1)两车同时开出,相向而行,经过多少小时相遇?
解:(1)设 两车行驶了xh相遇,
根据题意得 65x+85x=450,
解,得 x = 3.
答:两车经过3h相遇.
分析:等量关系:慢车路程+快车路程=甲乙之间的距离.
探究二:应用一元一次方程解决相遇问题
相遇
慢车行驶的路程65x
甲乙两地之间的距离450km
快车行驶的路程85x
甲
乙
线段图:
二、新知探究
(2)快车先开30min,两车相向而行,慢车行驶了多少小时两车相遇?
相遇
快车先开30min行驶的路程85×0.5
慢车行驶的路程65y
甲乙两地之间的距离450km
快车在慢车走时行驶的路程85y
解:(2)设慢车行驶了y小时两车相遇.
据题意得 65y+85(y+0.5)=450,
解,得 y= ??????????????????.
答:慢车行驶了??????????????????小时两车相遇.
?
相遇问题:
关于两人从两地出发相向而行的行程问题称为相遇问题,这类问题往往根据路程之和等于总路程列方程.
如图所示,甲的行程+乙的行程=两地相距的路程.
二、新知探究
知识归纳
二、新知探究
思考:操场一周是400米,小明每秒跑5米,小强每秒跑4米,两人绕跑道同时同地同向而行,他俩能相遇吗?
小强
小明
同时同地
同向而行
能相遇
探究三:环形跑道中的追及和相遇问题
分 析:
二、新知探究
操场一周是400米,小明每秒跑5米,小强骑自行车每秒15米.
(1)两人绕跑道同时同地同向而行,经过几秒钟两人第一次相遇?
(2)两人同时同地相背而行,则两个人何时相遇?
解:设经过x秒两人第一次相遇,
根据题意,得15x-5x=400,
解得 x=40.
答:经过40秒两人第一次相遇.
(2)设经过x秒两人第一次相遇,
根据题意,得 15x+5x=400,
解得 x=20 .
答:经过 20 秒两人第一次相遇.
跟踪练习
二、新知探究
环形跑道长s米,设v甲>v乙,经过t秒甲、乙第一次相遇.
一般有如下两种情形:
①同时同地、同向而行:
v甲t-v乙t=s.
②同时同地、背向而行:
v甲t+v乙t=s.
环形跑道问题
追及问题
相遇问题
知识归纳
解:设甲、乙两地距离是x千米,
由题意得 ????????????+??????????????????????=????????,
解得 x=286,
答:甲、乙两地的距离是286千米.
?
二、新知探究
分析:本题涉及水流速度:
顺水速度=船速+水速;逆水速度=船速-水速.
已知船在静水中的速度是24千米/时,水流速度是2千米/时,该船在甲、乙两地间行驶一个来回共用了24小时,求甲、乙两地的距离是多少?
做一做
1.顺(逆)水问题中的有关公式:
①顺水速度=静水中的速度+水流速度;
②逆水速度=静水中的速度-水流速度;
③顺水速度-逆水速度=2×水流速度.
2.顺(逆)风问题中的有关公式:
①顺风速度=无风速度+风速;
②逆风速度=无风速度-风速;
③顺风速度-逆风速度=2×风速.
二、新知探究
知识归纳
三、典例精析
例1:小明家离学校2.9千米.一天,小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,则小明爸爸从家出发几分钟后接到小明?
[解析] 设小明爸爸出发x分钟后接到小明.
可以画出线段图如右图所示.
解:设小明爸爸从家出发x分钟后接到小明,
由题意,得200x+60(x+5)=2900.
解这个方程,得x=10.
因此,小明爸爸从家出发10分钟后接到小明.
三、典例精析
例2:小明的爷爷每天都步行到距离家3.2千米的公园去打太极拳.周日早晨,爷爷出发半小时后,小明发现爷爷忘记带家门钥匙了,小明就骑自行车去给爷爷送钥匙.如果爷爷的速度是4千米/时,小明骑自行车的速度是12千米/时,当小明追上爷爷时,爷爷到公园了吗?
解:设小明用x小时追上爷爷.
因为3千米<3.2千米.
所以小明追上爷爷时,爷爷没有到公园.
三、典例精析
例3:一架飞机在两个城市之间飞行,当顺风飞行时需2.9 h,当逆风飞行时则需3.1 h.已知风速为20 km/h,求无风时飞机的航速和这两个城市之间的距离.
解:设无风时飞机的航速为x km/h,
根据题意,得 2.9(x+20)=3.1(x-20).
解这个方程,得 x=600.
则3.1(x-20)=1798.
因此,无风时飞机的航速为600 km/h,这两个城市之间的距离为1798 km.
2.小明骑自行车到学校上学,若每小时骑15千米,可早到10分钟,若每小时骑13千米,则迟到5分钟,设他家到学校的路程为x千米,下列方程正确的是( )
四、当堂练习
1.小明和小刚从相距25.2千米的两地同时相向而行,小明每小时走4千米,3小时后两人相遇,设小刚的速度为x千米/时,列方程得( )
A.4+3x=25.2 B.3×4+x=25.2
C.3(4+x)=25.2 D.3(x-4)=25.2
C
A
四、当堂练习
3.甲、乙两人在环形跑道上练习跑步,已知环形跑道一圈长400米,乙每秒跑6米,甲每秒跑8米.如果甲在乙前面8米处同时同向出发,那么经过几秒两人首次相遇( )
A.208秒 B.204秒 C.200秒 D.196秒
D
4.一列长30米的队伍以每分钟60米的速度向前行进,队尾一名同学用1分钟从队尾走到队头,这位同学走的路程为____米,速度是____米/分.
90
90
四、当堂练习
5.甲、乙两人赛跑,甲的速度是8米/秒,乙的速度是5米/秒,如果甲从起点处往后退20米,乙从起点处向前进10米,若甲、乙两人同时出发,则甲经过几秒钟追上乙?
解:设甲经过x秒追上乙.
由题意,得8x-5x=20+10.
解这个方程,得x=10.
因此,甲经过10秒追上乙.
四、当堂练习
6.A,B两地相距30千米.甲、乙两人分别从A,B两地同时出发,相向而行.已知甲比乙每小时多走1千米,经过2.5小时两人相遇,求甲、乙两人的速度.
解:设乙的速度为x千米/时,则甲的速度为(x+1)千米/时.
根据题意,得2.5x+2.5(x+1)=30.
解这个方程,得x=5.5.则x+1=6.5.
因此,甲、乙两人的速度分别为6.5千米/时、5.5千米/时.
四、当堂练习
7.一架飞机在两城市之间飞行,风速为24千米/时,顺风飞行需要2小时50分,逆风飞行需要3小时.求无风时飞机的飞行速度和两城之间的航程.
五、课堂小结
同向追
及问题
相向相
遇问题
应用一元一次方程
——追赶小明
同地不同时:甲路程=乙路程
同时不同地:甲路程+路程差=乙路程
甲的路程+乙的路程=总路程
六、作业布置
习题5.9
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
