2.1 二次函数 课件(共27张PPT)-2023-2024学年九年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 2.1 二次函数 课件(共27张PPT)-2023-2024学年九年级数学下册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览








文档简介
北师大版 数学 九年级下册
第二章 二次函数
1 二次函数
学习目标
1.理解二次函数的概念,掌握其一般形式.(重点)
2.会解决跟二次函数的概念有关的问题.
3.从实际问题出发列二次函数解析式,体验用函数思想去描述、研究变量之间变化规律的意义.(重、难点)
复习回顾
1.我们以前学过的函数的概念是什么?
如果变量y随着x而变化,并且对于x取的每一个值,y总有唯一的一个值与它对应,那么称y是x的函数.
函 数
2.我们学过哪些函数?
从上面的几种函数来看,每一种函数都有一般的形式,本节课我们将再学习一种新的函数.
一次函数
y=kx+b (k≠0)
反比例函数
(正比例函数) y=kx (k≠0)
一、创设情境,引入新知
节日的喷泉给人们带来喜庆,夏日的喷泉给人人们带来凉爽.你是否注意到喷泉水流所经过的路线?在观看篮球比赛时,你是是否注意过篮球入篮的路线?它会与某种函数有联系吗?
本章我们将要探索和研究刻画变量之间关系的一种新模型一二次函数.类似于以前所学的一次函数和反比例函数,我们也要借助图象发现二次函数的性质,并利用二次函数解决一些实际问题.
二、自主合作,探究新知
探究一:二次函数的定义
问题1:某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)问题中有那些变量?其中哪些是自变量?哪些是因变量?
变量:橙子树的棵数、橙子树之间的距离、橙子树接受阳光的多少、橙子的个数、橙子的质量等;
自变量:橙子树的棵数、橙子树之间的距离、橙子树接受阳光的多少等;因变量:橙子的个数、橙子的质量等.
二、自主合作,探究新知
(2)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(4)关系式y==-5x?+100x+60000中,y是x的函数吗?
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
果园共有(100+x)棵树,平均每棵树结(600-5x)个橙子.
y=(100+x)(600-5x) =-5x?+100x+60000.
对于x的每一个值,y都有唯一的一个对应值,即y是x的函数.
根据函数的定义判断.
问题2:银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量.在我国,利率的调整是由中国人民银行根据国民经济发展的情况而决定的.
二、自主合作,探究新知
设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存.如果存款是100元,那么请你写出两年后的本息和y(元)的表达式(不考虑利息税).
解:依题意得,一年后的本息和为:100+100x=100(1+x)
两年后本息和为:100(1+x)+100(1+x)x
所以,y 与x的关系式为:y=100(1+x)2
化简为:y=100x?+200x+100
根据函数的定义判断y是x的函数.
思考:关系式y=100x?+200x+100中,y是x的函数吗?
二、自主合作,探究新知
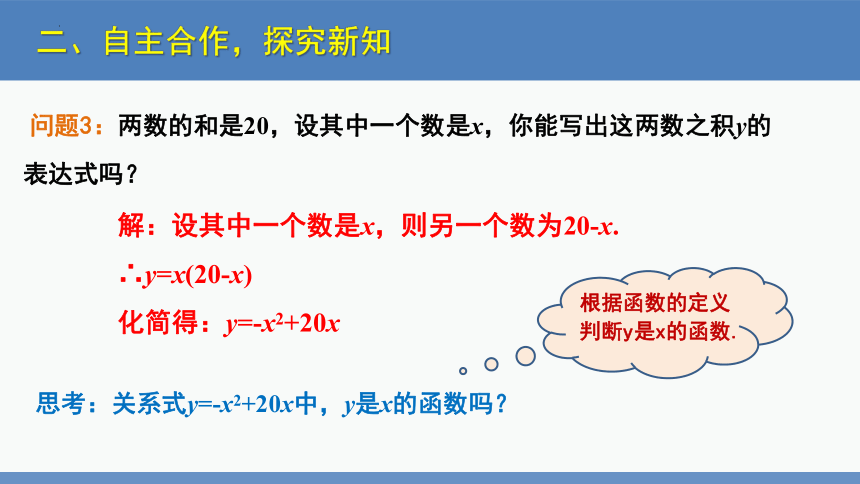
问题3:两数的和是20,设其中一个数是x,你能写出这两数之积y的表达式吗?
解:设其中一个数是x,则另一个数为20-x.
∴y=x(20-x)
化简得:y=-x2+20x
根据函数的定义判断y是x的函数.
思考:关系式y=-x2+20x中,y是x的函数吗?
二、自主合作,探究新知
前面求出的三个函数有什么共同点?
形如这样的函数叫做二次函数.
①y==-5x?+100x+60000;
②y=100x?+200x+100;
③y=-x2+20x.
想一想
①这些式子都是最高次数为2的函数;
②表达式右边都是关于x的整式.
你能类比一次函数和反比例函数,给出二次函数的定义吗?
二、自主合作,探究新知
二次函数的定义:
一般地,若两个变量x,y之间的对应关系可以表示成y=ax?+bx+c
(a,b,c是常数,a≠ 0)的形式,则称y是x的二次函数.
知识要点
你能举出一些二次函数的例子吗?
例如:①正方形面积A与边长a的关系A=a2;
②圆的面积与半径r的关系S=πr2;
③自由落体运动物体下落的高度h与下落时间t的关系h=????????gt2等也是二次函数.
?
二、自主合作,探究新知
二次函数一般形式:y=ax?+bx+c(a,b,c是常数,a≠0).
其中:a为二次项系数,ax2叫做二次项;
b为一次项系数,bx叫做一次项;
c为常数项.
注意:(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0(b,c可以为0);
(3)等式的右边最高次数为2,可以没有一次项和常数项,
但不能没有二次项.
知识要点
例1:下列函数中,是二次函数的有哪些?
① y=ax2+bx+c
② ????=????????(x-3)?????
③ y=x2
④ ????=????????????
⑤ y=x?+x?+25
⑥ y=(2x+3)??4x?
?
二、自主合作,探究新知
典型例题
不一定是,缺少a≠0的条件.
不是,等号右边是分式,不是整式.
不是,x的最高次数是3.
不是,化简后为y=12x+9,是一次函数.
二、自主合作,探究新知
判断一个函数是不是二次函数,要抓住二次函数的结构特征:(1)解析式是关于自变量的整式;
(2)自变量的最高次数是2;
(3)化简后二次项系数不为0.
除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式,如 ????=????????????,????=????????????+????????,?????=????????????+????等.
?
方法归纳
二、自主合作,探究新知
解得 m=3.
注意:不要忽略二次项系数a≠0这一限制条件,从而得出m=3或-3的错误答案.
解:由二次函数的定义可知,
例2: m取什么值时,此函数是二次函数?
典型例题
二、自主合作,探究新知
解: S=x(20-x) 化简得:S=-x2+20x,
∴ S是x的二次函数.
已知矩形的周长为40cm,回答下列问题:
(1)写出矩形的面积S与其一边x的关系,并判断S是不是x的二次函数?
做一做
(2)它的面积可能是100cm2吗?可能是75cm2吗?
令S=100,则100=-x2+20x,解得x1=x2=10;
令S=75,则75=-x2+20x,解得x1=15,x2=5.
思考:二次函数的一般式????=????????????+????????+????(????≠????)与前面我们学过的一元二次方程????????????+????????+????=????(????≠????)有什么联系和区别?
?
二、自主合作,探究新知
区别:前者是函数,后者是方程;等式另一边前者是y,后者是0.
知识要点
二次函数的一般式????=????????????+????????+????(????≠????)与一元二次方程????????????+????????+????=????(????≠????)的联系和区别:
?
联系:(1)等式一边都是????????????+????????+????且????≠????;
(2)方程????????????+????????+????=????可以看成是函数????=?????????????+????????+????中????=????时得到的.
?
(2)上述实际问题1~3中的三个函数的自变量的取值范围是什么?
问题1:y==-5x?+100x+60000;
问题2:y=100x?+200x+100;
问题3:y=-x2+20x.
二、自主合作,探究新知
在实际问题中,二次函数自变量的取值范围会有一些限制.
议一议:(1)二次函数y=ax?+bx+c(a,b,c是常数,a≠ 0)中,自变量x可以取哪些值?
③∵由题意得?????????????>????????>???? ,∴0?
二次函数的自变量的取值范围是所有实数.
②x>0.
①∵由题意得?????????????????????>????????>???? ,
∴0?
探究二:二次函数的自变量取值范围
二、自主合作,探究新知
探究三:列二次函数关系式
例3:一个正方形的边长是12cm,若从中挖去一个长为2xcm,宽为(x+1)cm的小长方形.剩余部分的面积为ycm2.写出y与x之间的函数关系式和x的取值范围,并指出y是x的什么函数?
解:由题意得y=122-2x(x+1)=-2x2-2x+144,
又∵x+1<2x≤12,
∴1即y=-2x2-2x+144(1 ∴y是x的二次函数.
分析:本题中的数量关系是:剩余面积=正方形面积-长方形面积.
1.下列函数中,????是????的二次函数的是 ( )
A.y=2x+1 B.????=????????+????????
C.????????=3x+1 D.????=????????+????????
?
三、即学即练,应用知识
C
B
2.函数 ????=(?????????)????????+?????????+?????是二次函数的条件是( )
A . ????,????是常数,且????≠???? B . ????,????是常数,且????≠????
C. ????,????是常数,且????≠???? D .?????,????为任何实数
?
3.二次函数????=????(????+????)?????????的二次项是____,一次项系数是_____,
常数项是 .
?
三、即学即练,应用知识
2x2
4. 已知函数 y=3x2m-1-5 ,当m=__时,y是关于x的二次函数 .
5.二次函数y=x2-2x-4,当x=2时,函数值y= ;当x= 时,函数y的值为-1.
-4
3或-1
8
5
6.菱形的两条对角线的和为 26cm,则菱形的面积S(cm2)与一条对角线的长x(cm)之间的函数关系式为 ,自变量x的取值范围是 .
0????=?????????????????+????????????
?
三、即学即练,应用知识
7.一个直角三角形的两条直角边之和为18,其中一条直角边的长为x.
(1)求这个直角三角形的面积S与x的函数关系式,并指出自变量x的取值范围;
(2)当x=2时,求S的值.
解:(1)由题意得S=????????x(18-x)=-????????????????+????????,
自变量x的取值范围是0(2)当x=2时,????=?????????×????????+????×????=16.
?
四、课堂小结
定 义
一般形式
右边是整式;
自变量的指数是2;
二次项系数a ≠0.
????=????????????;
????=????????????+????????;
????=????????????+????(?????≠????,????,????,????是常数).
?
特殊形式
二次函数
????=????????????+????????+????(?????≠????,????,????,????是常数)
?
1.下列表达式中,一定为二次函数的是( )A.y=x-1 B.y=ax2+bx+cC.s=2t2-2t+3 D.y=x2+????????
?
五、当堂达标检测
2.下列关系中,是二次函数关系的是( )
A.当距离s一定时,汽车行驶的时间t与速度v之间的关系
B.在弹性限度内,弹簧的长度y与所挂物体的质量x之间的关系
C.圆的面积S与圆的半径r之间的关系
D.正方形的周长C与边长a之间的关系
C
C
3.一台机器原价 40 万元,每次降价的百分率为x,那么连续两次降价后的价格y(万元)与x之间的函数关系为( )
A.y=40(1-x) B.y=40(1-x2)
C. y=40(1-x)2 D.y=40(1+x)2
五、当堂达标检测
C
4.把y=(2-3x)(6+x)变成y=ax?+bx+c的形式,二次项为_____,一次项系数为______,常数项为 .
-3x2
-16
12
5.二次函数y=-x2+x+1,当x=-1时,y= ,当y=1时,x= .
-1
0或1
五、当堂达标检测
6.矩形的周长为16 cm,它的一边长为x(cm),面积为y(cm2).
(1)求y与x之间的函数解析式及自变量x的取值范围;
(2)求当x=3时矩形的面积.
解:(1)????=(????-????)????=-????????+??????????(????<????<????).
(2)当????=????时,????=-????????+????×????=????????(??????????????).
?
五、当堂达标检测
7.正方形的边长是4 cm,当边长增加x cm时,面积增加y cm2.
(1)写出y与x之间函数关系式;
(2)当边长增加了3cm时,面积增加了多少?
(3)当面积增加了48cm2时,边长增加了多少?
解:(1)y=(x+4)2-42=x2+8x(x>0) ,
∴y与x之间函数关系式为:y==x2+8x(x>0) .
(2)当x=3时,y=32+8×3=33 cm2,
∴面积增加33 cm2 .
(3)当y=48 cm2时,x2+8x=48,解得x1=4,x2=-12(舍),
∴边长增加了4 cm.
教材习题2.1;
六、布置作业
第二章 二次函数
1 二次函数
学习目标
1.理解二次函数的概念,掌握其一般形式.(重点)
2.会解决跟二次函数的概念有关的问题.
3.从实际问题出发列二次函数解析式,体验用函数思想去描述、研究变量之间变化规律的意义.(重、难点)
复习回顾
1.我们以前学过的函数的概念是什么?
如果变量y随着x而变化,并且对于x取的每一个值,y总有唯一的一个值与它对应,那么称y是x的函数.
函 数
2.我们学过哪些函数?
从上面的几种函数来看,每一种函数都有一般的形式,本节课我们将再学习一种新的函数.
一次函数
y=kx+b (k≠0)
反比例函数
(正比例函数) y=kx (k≠0)
一、创设情境,引入新知
节日的喷泉给人们带来喜庆,夏日的喷泉给人人们带来凉爽.你是否注意到喷泉水流所经过的路线?在观看篮球比赛时,你是是否注意过篮球入篮的路线?它会与某种函数有联系吗?
本章我们将要探索和研究刻画变量之间关系的一种新模型一二次函数.类似于以前所学的一次函数和反比例函数,我们也要借助图象发现二次函数的性质,并利用二次函数解决一些实际问题.
二、自主合作,探究新知
探究一:二次函数的定义
问题1:某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)问题中有那些变量?其中哪些是自变量?哪些是因变量?
变量:橙子树的棵数、橙子树之间的距离、橙子树接受阳光的多少、橙子的个数、橙子的质量等;
自变量:橙子树的棵数、橙子树之间的距离、橙子树接受阳光的多少等;因变量:橙子的个数、橙子的质量等.
二、自主合作,探究新知
(2)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(4)关系式y==-5x?+100x+60000中,y是x的函数吗?
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
果园共有(100+x)棵树,平均每棵树结(600-5x)个橙子.
y=(100+x)(600-5x) =-5x?+100x+60000.
对于x的每一个值,y都有唯一的一个对应值,即y是x的函数.
根据函数的定义判断.
问题2:银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量.在我国,利率的调整是由中国人民银行根据国民经济发展的情况而决定的.
二、自主合作,探究新知
设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存.如果存款是100元,那么请你写出两年后的本息和y(元)的表达式(不考虑利息税).
解:依题意得,一年后的本息和为:100+100x=100(1+x)
两年后本息和为:100(1+x)+100(1+x)x
所以,y 与x的关系式为:y=100(1+x)2
化简为:y=100x?+200x+100
根据函数的定义判断y是x的函数.
思考:关系式y=100x?+200x+100中,y是x的函数吗?
二、自主合作,探究新知
问题3:两数的和是20,设其中一个数是x,你能写出这两数之积y的表达式吗?
解:设其中一个数是x,则另一个数为20-x.
∴y=x(20-x)
化简得:y=-x2+20x
根据函数的定义判断y是x的函数.
思考:关系式y=-x2+20x中,y是x的函数吗?
二、自主合作,探究新知
前面求出的三个函数有什么共同点?
形如这样的函数叫做二次函数.
①y==-5x?+100x+60000;
②y=100x?+200x+100;
③y=-x2+20x.
想一想
①这些式子都是最高次数为2的函数;
②表达式右边都是关于x的整式.
你能类比一次函数和反比例函数,给出二次函数的定义吗?
二、自主合作,探究新知
二次函数的定义:
一般地,若两个变量x,y之间的对应关系可以表示成y=ax?+bx+c
(a,b,c是常数,a≠ 0)的形式,则称y是x的二次函数.
知识要点
你能举出一些二次函数的例子吗?
例如:①正方形面积A与边长a的关系A=a2;
②圆的面积与半径r的关系S=πr2;
③自由落体运动物体下落的高度h与下落时间t的关系h=????????gt2等也是二次函数.
?
二、自主合作,探究新知
二次函数一般形式:y=ax?+bx+c(a,b,c是常数,a≠0).
其中:a为二次项系数,ax2叫做二次项;
b为一次项系数,bx叫做一次项;
c为常数项.
注意:(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0(b,c可以为0);
(3)等式的右边最高次数为2,可以没有一次项和常数项,
但不能没有二次项.
知识要点
例1:下列函数中,是二次函数的有哪些?
① y=ax2+bx+c
② ????=????????(x-3)?????
③ y=x2
④ ????=????????????
⑤ y=x?+x?+25
⑥ y=(2x+3)??4x?
?
二、自主合作,探究新知
典型例题
不一定是,缺少a≠0的条件.
不是,等号右边是分式,不是整式.
不是,x的最高次数是3.
不是,化简后为y=12x+9,是一次函数.
二、自主合作,探究新知
判断一个函数是不是二次函数,要抓住二次函数的结构特征:(1)解析式是关于自变量的整式;
(2)自变量的最高次数是2;
(3)化简后二次项系数不为0.
除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式,如 ????=????????????,????=????????????+????????,?????=????????????+????等.
?
方法归纳
二、自主合作,探究新知
解得 m=3.
注意:不要忽略二次项系数a≠0这一限制条件,从而得出m=3或-3的错误答案.
解:由二次函数的定义可知,
例2: m取什么值时,此函数是二次函数?
典型例题
二、自主合作,探究新知
解: S=x(20-x) 化简得:S=-x2+20x,
∴ S是x的二次函数.
已知矩形的周长为40cm,回答下列问题:
(1)写出矩形的面积S与其一边x的关系,并判断S是不是x的二次函数?
做一做
(2)它的面积可能是100cm2吗?可能是75cm2吗?
令S=100,则100=-x2+20x,解得x1=x2=10;
令S=75,则75=-x2+20x,解得x1=15,x2=5.
思考:二次函数的一般式????=????????????+????????+????(????≠????)与前面我们学过的一元二次方程????????????+????????+????=????(????≠????)有什么联系和区别?
?
二、自主合作,探究新知
区别:前者是函数,后者是方程;等式另一边前者是y,后者是0.
知识要点
二次函数的一般式????=????????????+????????+????(????≠????)与一元二次方程????????????+????????+????=????(????≠????)的联系和区别:
?
联系:(1)等式一边都是????????????+????????+????且????≠????;
(2)方程????????????+????????+????=????可以看成是函数????=?????????????+????????+????中????=????时得到的.
?
(2)上述实际问题1~3中的三个函数的自变量的取值范围是什么?
问题1:y==-5x?+100x+60000;
问题2:y=100x?+200x+100;
问题3:y=-x2+20x.
二、自主合作,探究新知
在实际问题中,二次函数自变量的取值范围会有一些限制.
议一议:(1)二次函数y=ax?+bx+c(a,b,c是常数,a≠ 0)中,自变量x可以取哪些值?
③∵由题意得?????????????>????????>???? ,∴0
二次函数的自变量的取值范围是所有实数.
②x>0.
①∵由题意得?????????????????????>????????>???? ,
∴0
探究二:二次函数的自变量取值范围
二、自主合作,探究新知
探究三:列二次函数关系式
例3:一个正方形的边长是12cm,若从中挖去一个长为2xcm,宽为(x+1)cm的小长方形.剩余部分的面积为ycm2.写出y与x之间的函数关系式和x的取值范围,并指出y是x的什么函数?
解:由题意得y=122-2x(x+1)=-2x2-2x+144,
又∵x+1<2x≤12,
∴1
分析:本题中的数量关系是:剩余面积=正方形面积-长方形面积.
1.下列函数中,????是????的二次函数的是 ( )
A.y=2x+1 B.????=????????+????????
C.????????=3x+1 D.????=????????+????????
?
三、即学即练,应用知识
C
B
2.函数 ????=(?????????)????????+?????????+?????是二次函数的条件是( )
A . ????,????是常数,且????≠???? B . ????,????是常数,且????≠????
C. ????,????是常数,且????≠???? D .?????,????为任何实数
?
3.二次函数????=????(????+????)?????????的二次项是____,一次项系数是_____,
常数项是 .
?
三、即学即练,应用知识
2x2
4. 已知函数 y=3x2m-1-5 ,当m=__时,y是关于x的二次函数 .
5.二次函数y=x2-2x-4,当x=2时,函数值y= ;当x= 时,函数y的值为-1.
-4
3或-1
8
5
6.菱形的两条对角线的和为 26cm,则菱形的面积S(cm2)与一条对角线的长x(cm)之间的函数关系式为 ,自变量x的取值范围是 .
0
?
三、即学即练,应用知识
7.一个直角三角形的两条直角边之和为18,其中一条直角边的长为x.
(1)求这个直角三角形的面积S与x的函数关系式,并指出自变量x的取值范围;
(2)当x=2时,求S的值.
解:(1)由题意得S=????????x(18-x)=-????????????????+????????,
自变量x的取值范围是0
?
四、课堂小结
定 义
一般形式
右边是整式;
自变量的指数是2;
二次项系数a ≠0.
????=????????????;
????=????????????+????????;
????=????????????+????(?????≠????,????,????,????是常数).
?
特殊形式
二次函数
????=????????????+????????+????(?????≠????,????,????,????是常数)
?
1.下列表达式中,一定为二次函数的是( )A.y=x-1 B.y=ax2+bx+cC.s=2t2-2t+3 D.y=x2+????????
?
五、当堂达标检测
2.下列关系中,是二次函数关系的是( )
A.当距离s一定时,汽车行驶的时间t与速度v之间的关系
B.在弹性限度内,弹簧的长度y与所挂物体的质量x之间的关系
C.圆的面积S与圆的半径r之间的关系
D.正方形的周长C与边长a之间的关系
C
C
3.一台机器原价 40 万元,每次降价的百分率为x,那么连续两次降价后的价格y(万元)与x之间的函数关系为( )
A.y=40(1-x) B.y=40(1-x2)
C. y=40(1-x)2 D.y=40(1+x)2
五、当堂达标检测
C
4.把y=(2-3x)(6+x)变成y=ax?+bx+c的形式,二次项为_____,一次项系数为______,常数项为 .
-3x2
-16
12
5.二次函数y=-x2+x+1,当x=-1时,y= ,当y=1时,x= .
-1
0或1
五、当堂达标检测
6.矩形的周长为16 cm,它的一边长为x(cm),面积为y(cm2).
(1)求y与x之间的函数解析式及自变量x的取值范围;
(2)求当x=3时矩形的面积.
解:(1)????=(????-????)????=-????????+??????????(????<????<????).
(2)当????=????时,????=-????????+????×????=????????(??????????????).
?
五、当堂达标检测
7.正方形的边长是4 cm,当边长增加x cm时,面积增加y cm2.
(1)写出y与x之间函数关系式;
(2)当边长增加了3cm时,面积增加了多少?
(3)当面积增加了48cm2时,边长增加了多少?
解:(1)y=(x+4)2-42=x2+8x(x>0) ,
∴y与x之间函数关系式为:y==x2+8x(x>0) .
(2)当x=3时,y=32+8×3=33 cm2,
∴面积增加33 cm2 .
(3)当y=48 cm2时,x2+8x=48,解得x1=4,x2=-12(舍),
∴边长增加了4 cm.
教材习题2.1;
六、布置作业
