5.4 二次函数与一元二次方程 课件(共32张PPT)-2023-2024学年九年级数学下册同步精品课堂(苏科版)
文档属性
| 名称 | 5.4 二次函数与一元二次方程 课件(共32张PPT)-2023-2024学年九年级数学下册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
5.4 二次函数与一元二次方程
第5章 二次函数
教学目标
01
理解二次函数y=ax2+bx+c与一元二次方程ax2+bx+c=0的关系,能根据二次函数y=ax2+bx+c的图像确定一元二次方程ax2+bx+c=0的根的情况
02
掌握直线与抛物线的交点问题——会求直线与抛物线的交点坐标,并会判断直线与抛物线的交点个数
图像法确定一元二次方程的根的情况
Q1:二次函数y=ax2+bx+c与一元二次方程ax2+bx+c=0有怎样的关系?
令y=0,得:ax2+bx+c=0
当二次函数y=ax2+bx+c的y=0时,有一元二次方程ax2+bx+c=0
01
问题引入
Q2:观察y=x2-3x-4的图像,回答问题:
(1)二次函数y=x2-3x-4的图像与x轴的交点A、B的坐标分别是A_______,B_______;
(2)当x=_______时,函数的值y=0;
(3)求一元二次方程x2-3x-4=0的解;
(-1,0)
(4,0)
-1或4
x=-1或x=4
01
问题引入
(4)二次函数y=x2-3x-4与x轴的交点,与一元二次方程x2-3x-4=0的解之间有什么关系?
01
问题引入
二次函数y=ax2+bx+c的图像与x轴交点的横坐标
=
一元二次方程ax2+bx+c=0的解
Q3:(1)观察二次函数y=x2+x-2、y=x2-6x+9、y=x2-x+1的图像,分别说出一元二次方程x2+x-2=0、x2-6x+9=0、x2-x+1=0的根的情况。
两个交点
→两个不同的实数根
一个交点
→两个相同的实数根
没有交点
→没有实数根
01
问题引入
(2)利用判别式法检验(1)中结论是否正确。
【分析】
对于x2+x-2=0,=9>0,方程有两个不同的实数根;
对于x2-6x+9=0,=0,方程有两个相同的实数根;
对于x2-x+1=0,=-3<0,方程没有实数根。
01
问题引入
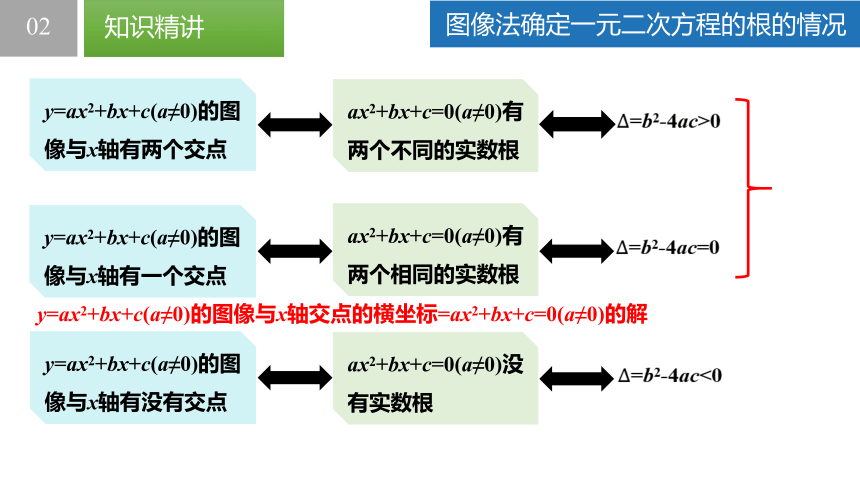
y=ax2+bx+c(a≠0)的图像与x轴有两个交点
y=ax2+bx+c(a≠0)的图像与x轴有一个交点
y=ax2+bx+c(a≠0)的图像与x轴有没有交点
ax2+bx+c=0(a≠0)有两个不同的实数根
ax2+bx+c=0(a≠0)有两个相同的实数根
ax2+bx+c=0(a≠0)没有实数根
=b2-4ac>0
=b2-4ac=0
=b2-4ac<0
图像法确定一元二次方程的根的情况
02
知识精讲
y=ax2+bx+c(a≠0)的图像与x轴交点的横坐标=ax2+bx+c=0(a≠0)的解
图像法确定一元二次方程的根的情况
02
知识精讲
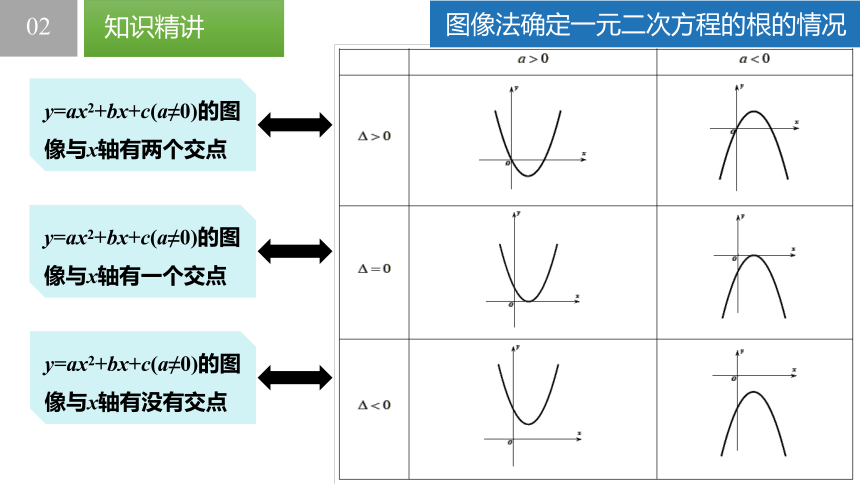
y=ax2+bx+c(a≠0)的图像与x轴有两个交点
y=ax2+bx+c(a≠0)的图像与x轴有一个交点
y=ax2+bx+c(a≠0)的图像与x轴有没有交点
例1、求二次函数y=(x-5)(x-7)的图像与x轴的交点坐标。
解:令y=0,即(x-5)(x-7)=0,解得:x=5或x=7,
∴二次函数y=(x-5)(x-7)的图像与x轴的交点坐标为(5,0)和(7,0)。
03
典例精析
例2、二次函数y=x2-6x+n的部分图像如图所示,若关于x的一元二次方程x -6x+n=0的一个解x1=1,求另一个解x2。
解:∵二次函数的图像与x轴的一个交点为(1,0),且对称轴为x=3,
∴另一个交点为(5,0),
∵y=ax2+bx+c(a≠0)的图像与x轴交点的横坐标=ax2+bx+c=0(a≠0)的解,
∴x -6x+n=0的另一个解x2=5。
03
典例精析
例3、(1)求抛物线y=kx2+(2k+1)x+2的图像与x轴的两个交点;
(2)若(1)中两个交点的横坐标均为整数,且k为正整数,试求出该二次函数的表达式;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,直接写出定点的坐标。
解:(1)令y=0,即kx2+(2k+1)x+2=(kx+1)(x+2)=0,
解得:x=-或x=-2,
∴抛物线y=kx2+(2k+1)x+2图像与x轴的两个交点为(-,0),(-2,0);
03
典例精析
例3、(1)求抛物线y=kx2+(2k+1)x+2图像与x轴的两个交点;
(2)若(1)中两个交点的横坐标均为整数,且k为正整数,试求出该二次函数的表达式;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,直接写出定点的坐标。
(2)∵(1)中两个交点的横坐标均为整数,且k为正整数,
∴k=1,
∴y=x2+3x+2;
03
典例精析
03
典例精析
例3、(1)求抛物线y=kx2+(2k+1)x+2图像与x轴的两个交点;
(2)若(1)中两个交点的横坐标均为整数,且k为正整数,试求出该二次函数的表达式;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,直接写出定点的坐标。
(3)解:∵y=kx2+(2k+1)x+2=(x2+2x)k+x+2恒过定点,
∴x2+2x=0,
∴x=-2或x=0,
∴定点的坐标为(-2,0)或(0,2)。
例4、抛物线y=ax2-2x+3与x轴有两个交点,求a的取值范围。
解:∵y=ax2-2x+3与x轴有两个交点,
∴=4-12a>0且a≠0,解得:a<且a≠0。
03
典例精析
例5、已知抛物线y=4x2+2x+c,且当-1解:(2)∵当-1∴①当=4-16c=0时,解得:c=,
即y=4x2+2x+,令y=0,解得:x=-,成立;
②当=4-16c>0时,解得:c<,
当x=-1时,y=2+c≤0,当x=1时,y=6+c>0,解得:-6综上,c=或-603
典例精析
例6、已知关于x的一元二次方程:x2-(m-3)x-m=0
(1)试判断原方程根的情况;
(2)若抛物线y=x2-(m-3)x-m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由。(友情提示:AB=|x1-x2|)
解:(1)∵=(m-3)2+4m=m2-2m+9=(m-1)2+8>0,
∴原方程有两个不同的根;
03
典例精析
例6、已知关于x的一元二次方程:x2-(m-3)x-m=0
(1)试判断原方程根的情况;
(2)若抛物线y=x2-(m-3)x-m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由。(友情提示:AB=|x1-x2|)
(2)存在,理由如下:根据韦达定理:x1+x2=m-3,x1+x2=-m,
∴AB=|x1-x2|===,∴当m=1时,AB取最小值=2。
03
典例精析
直线与抛物线的交点问题
Q1:求直线y=1与抛物线y=x2-3x+3的交点坐标
直线与抛物线联立,化简可得一元二次方程
解:联立,得:x2-3x+3=1,
【也可看作直接将y=1代入y=x2-3x+3】
即x2-3x+2=0,(x-1)(x-2)=0,
解得:x=1或x=2,则直线与抛物线的交点坐标为(1,1),(2,1)。
01
问题引入
Q2:求直线y=x+1与抛物线y=x2-4x+7的交点坐标
解:联立,得:x2-4x+7=x+1,
即x2-5x+6=0,(x-2)(x-3)=0,
解得:x=2或x=3,则直线与抛物线的交点坐标为(2,3),(3,4)。
01
问题引入
(一)求直线y=kx+b(k≠0)与抛物线y=ax2+bx+c(a≠0)的交点坐标:
直线与抛物线的交点问题
联立,得一元二次方程:ax2+(b-k)x+c-b=0,
在方程有解的情况下,解一元二次方程得:交点的横坐标,
将横坐标代入直线方程得:交点的纵坐标。
02
知识精讲
直线与抛物线的交点问题
∵联立所得的一元二次方程的实数根=交点的横坐标,
∴交点个数可通过联立所得的一元二次方程的根的情况判断;
02
知识精讲
(二)判断直线y=kx+b(k≠0)与抛物线y=ax2+bx+c(a≠0)的交点个数:
(1)当>0时,两个不同的实数根→直线与抛物线有两个不同的交点,
(2)当=0时,两个相同的实数根→直线与抛物线有一个交点,
(3)当<0时,没有实数根→直线与抛物线没有交点。
例1、抛物线与直线y=m有交点,图中抛物线的表达式为y=ax +bx+c,根据图像判断下列方程根的情况。
(1)方程ax +bx+c=0的两根分别为__________________;
(2)方程ax +bx+c-3=0的两根分别为__________________;
(3)方程ax +bx+c=2的根的情况是__________________;
(4)方程ax +bx+c=4的根的情况是__________________。
x1=-2.5,x2=0.5
可以看作:抛物线y=ax +bx+c与直线y=3联立所得,
故方程的两根=抛物线y=ax +bx+c与直线y=3交点的横坐标。
x1=-1,x2=-1
03
典例精析
例1、抛物线与直线y=m有交点,图中抛物线的表达式为y=ax +bx+c,根据图像判断下列方程根的情况。
(1)方程ax +bx+c=0的两根分别为__________________;
(2)方程ax +bx+c-3=0的两根分别为__________________;
(3)方程ax +bx+c=2的根的情况是__________________;
(4)方程ax +bx+c=4的根的情况是__________________。
可以看作:抛物线y=ax +bx+c与直线y=2联立所得,
故方程的根的情况需分析抛物线y=ax +bx+c与直线y=2的交点情况。
03
典例精析
有两个不同的实数根
x1=-2.5,x2=0.5
x1=-1,x2=-1
例1、抛物线与直线y=m有交点,图中抛物线的表达式为y=ax +bx+c,根据图像判断下列方程根的情况。
(1)方程ax +bx+c=0的两根分别为__________________;
(2)方程ax +bx+c-3=0的两根分别为__________________;
(3)方程ax +bx+c=2的根的情况是__________________;
(4)方程ax +bx+c=4的根的情况是__________________。
可以看作:抛物线y=ax +bx+c与直线y=4联立所得,
故方程的根的情况需分析抛物线y=ax +bx+c与直线y=4的交点情况。
03
典例精析
有两个不同的实数根
x1=-2.5,x2=0.5
x1=-1,x2=-1
没有实数根
例2、(1)求直线y=x+1与抛物线y=x2-1的交点坐标;
(2)求直线y=2x-6与抛物线y=2x -6x+4的交点坐标。
解:(1)联立,得:x2-1=x+1,
即x2-x-2=0,(x+1)(x-2)=0,
解得:x=-1或x=2,则直线与抛物线的交点坐标为(-1,0),(2,3);
03
典例精析
例2、(1)求直线y=x+1与抛物线y=x2-1的交点坐标;
(2)求直线y=2x-6与抛物线y=2x -6x+4的交点坐标。
(2)联立,得:2x -6x+4=2x-6,即x2-4x+5=0,
∵=16-20<0,
∴直线与抛物线无交点。
03
典例精析
例3、已知a,b是关于x的方程(x-a)(x-b)=2的两个根,其中aA. a<α<βC. αB
可以看作:
抛物线y=(x-a)(x-b)与直线y=2联立所得
03
典例精析
课后总结
y=ax2+bx+c(a≠0)的图像与x轴有两个交点
y=ax2+bx+c(a≠0)的图像与x轴有一个交点
y=ax2+bx+c(a≠0)的图像与x轴有没有交点
ax2+bx+c=0(a≠0)有两个不同的实数根
ax2+bx+c=0(a≠0)有两个相同的实数根
ax2+bx+c=0(a≠0)没有实数根
=b2-4ac>0
=b2-4ac=0
=b2-4ac<0
y=ax2+bx+c(a≠0)的图像与x轴交点的横坐标=ax2+bx+c=0(a≠0)的解
图像法确定一元二次方程的根的情况:
课后总结
直线与抛物线的交点问题:
(一)交点坐标
联立,得一元二次方程:ax2+(b-k)x+c-b=0,
在方程有解的情况下,解一元二次方程得:交点的横坐标,
将横坐标代入直线方程得:交点的纵坐标。
(二)交点个数
交点个数可通过联立所得的一元二次方程的根的情况判断:
(1)当>0时,两个不同的实数根→直线与抛物线有两个不同的交点,
(2)当=0时,两个相同的实数根→直线与抛物线有一个交点,
(3)当<0时,没有实数根→直线与抛物线没有交点。
5.4 二次函数与一元二次方程
第5章 二次函数
教学目标
01
理解二次函数y=ax2+bx+c与一元二次方程ax2+bx+c=0的关系,能根据二次函数y=ax2+bx+c的图像确定一元二次方程ax2+bx+c=0的根的情况
02
掌握直线与抛物线的交点问题——会求直线与抛物线的交点坐标,并会判断直线与抛物线的交点个数
图像法确定一元二次方程的根的情况
Q1:二次函数y=ax2+bx+c与一元二次方程ax2+bx+c=0有怎样的关系?
令y=0,得:ax2+bx+c=0
当二次函数y=ax2+bx+c的y=0时,有一元二次方程ax2+bx+c=0
01
问题引入
Q2:观察y=x2-3x-4的图像,回答问题:
(1)二次函数y=x2-3x-4的图像与x轴的交点A、B的坐标分别是A_______,B_______;
(2)当x=_______时,函数的值y=0;
(3)求一元二次方程x2-3x-4=0的解;
(-1,0)
(4,0)
-1或4
x=-1或x=4
01
问题引入
(4)二次函数y=x2-3x-4与x轴的交点,与一元二次方程x2-3x-4=0的解之间有什么关系?
01
问题引入
二次函数y=ax2+bx+c的图像与x轴交点的横坐标
=
一元二次方程ax2+bx+c=0的解
Q3:(1)观察二次函数y=x2+x-2、y=x2-6x+9、y=x2-x+1的图像,分别说出一元二次方程x2+x-2=0、x2-6x+9=0、x2-x+1=0的根的情况。
两个交点
→两个不同的实数根
一个交点
→两个相同的实数根
没有交点
→没有实数根
01
问题引入
(2)利用判别式法检验(1)中结论是否正确。
【分析】
对于x2+x-2=0,=9>0,方程有两个不同的实数根;
对于x2-6x+9=0,=0,方程有两个相同的实数根;
对于x2-x+1=0,=-3<0,方程没有实数根。
01
问题引入
y=ax2+bx+c(a≠0)的图像与x轴有两个交点
y=ax2+bx+c(a≠0)的图像与x轴有一个交点
y=ax2+bx+c(a≠0)的图像与x轴有没有交点
ax2+bx+c=0(a≠0)有两个不同的实数根
ax2+bx+c=0(a≠0)有两个相同的实数根
ax2+bx+c=0(a≠0)没有实数根
=b2-4ac>0
=b2-4ac=0
=b2-4ac<0
图像法确定一元二次方程的根的情况
02
知识精讲
y=ax2+bx+c(a≠0)的图像与x轴交点的横坐标=ax2+bx+c=0(a≠0)的解
图像法确定一元二次方程的根的情况
02
知识精讲
y=ax2+bx+c(a≠0)的图像与x轴有两个交点
y=ax2+bx+c(a≠0)的图像与x轴有一个交点
y=ax2+bx+c(a≠0)的图像与x轴有没有交点
例1、求二次函数y=(x-5)(x-7)的图像与x轴的交点坐标。
解:令y=0,即(x-5)(x-7)=0,解得:x=5或x=7,
∴二次函数y=(x-5)(x-7)的图像与x轴的交点坐标为(5,0)和(7,0)。
03
典例精析
例2、二次函数y=x2-6x+n的部分图像如图所示,若关于x的一元二次方程x -6x+n=0的一个解x1=1,求另一个解x2。
解:∵二次函数的图像与x轴的一个交点为(1,0),且对称轴为x=3,
∴另一个交点为(5,0),
∵y=ax2+bx+c(a≠0)的图像与x轴交点的横坐标=ax2+bx+c=0(a≠0)的解,
∴x -6x+n=0的另一个解x2=5。
03
典例精析
例3、(1)求抛物线y=kx2+(2k+1)x+2的图像与x轴的两个交点;
(2)若(1)中两个交点的横坐标均为整数,且k为正整数,试求出该二次函数的表达式;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,直接写出定点的坐标。
解:(1)令y=0,即kx2+(2k+1)x+2=(kx+1)(x+2)=0,
解得:x=-或x=-2,
∴抛物线y=kx2+(2k+1)x+2图像与x轴的两个交点为(-,0),(-2,0);
03
典例精析
例3、(1)求抛物线y=kx2+(2k+1)x+2图像与x轴的两个交点;
(2)若(1)中两个交点的横坐标均为整数,且k为正整数,试求出该二次函数的表达式;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,直接写出定点的坐标。
(2)∵(1)中两个交点的横坐标均为整数,且k为正整数,
∴k=1,
∴y=x2+3x+2;
03
典例精析
03
典例精析
例3、(1)求抛物线y=kx2+(2k+1)x+2图像与x轴的两个交点;
(2)若(1)中两个交点的横坐标均为整数,且k为正整数,试求出该二次函数的表达式;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,直接写出定点的坐标。
(3)解:∵y=kx2+(2k+1)x+2=(x2+2x)k+x+2恒过定点,
∴x2+2x=0,
∴x=-2或x=0,
∴定点的坐标为(-2,0)或(0,2)。
例4、抛物线y=ax2-2x+3与x轴有两个交点,求a的取值范围。
解:∵y=ax2-2x+3与x轴有两个交点,
∴=4-12a>0且a≠0,解得:a<且a≠0。
03
典例精析
例5、已知抛物线y=4x2+2x+c,且当-1
即y=4x2+2x+,令y=0,解得:x=-,成立;
②当=4-16c>0时,解得:c<,
当x=-1时,y=2+c≤0,当x=1时,y=6+c>0,解得:-6
典例精析
例6、已知关于x的一元二次方程:x2-(m-3)x-m=0
(1)试判断原方程根的情况;
(2)若抛物线y=x2-(m-3)x-m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由。(友情提示:AB=|x1-x2|)
解:(1)∵=(m-3)2+4m=m2-2m+9=(m-1)2+8>0,
∴原方程有两个不同的根;
03
典例精析
例6、已知关于x的一元二次方程:x2-(m-3)x-m=0
(1)试判断原方程根的情况;
(2)若抛物线y=x2-(m-3)x-m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由。(友情提示:AB=|x1-x2|)
(2)存在,理由如下:根据韦达定理:x1+x2=m-3,x1+x2=-m,
∴AB=|x1-x2|===,∴当m=1时,AB取最小值=2。
03
典例精析
直线与抛物线的交点问题
Q1:求直线y=1与抛物线y=x2-3x+3的交点坐标
直线与抛物线联立,化简可得一元二次方程
解:联立,得:x2-3x+3=1,
【也可看作直接将y=1代入y=x2-3x+3】
即x2-3x+2=0,(x-1)(x-2)=0,
解得:x=1或x=2,则直线与抛物线的交点坐标为(1,1),(2,1)。
01
问题引入
Q2:求直线y=x+1与抛物线y=x2-4x+7的交点坐标
解:联立,得:x2-4x+7=x+1,
即x2-5x+6=0,(x-2)(x-3)=0,
解得:x=2或x=3,则直线与抛物线的交点坐标为(2,3),(3,4)。
01
问题引入
(一)求直线y=kx+b(k≠0)与抛物线y=ax2+bx+c(a≠0)的交点坐标:
直线与抛物线的交点问题
联立,得一元二次方程:ax2+(b-k)x+c-b=0,
在方程有解的情况下,解一元二次方程得:交点的横坐标,
将横坐标代入直线方程得:交点的纵坐标。
02
知识精讲
直线与抛物线的交点问题
∵联立所得的一元二次方程的实数根=交点的横坐标,
∴交点个数可通过联立所得的一元二次方程的根的情况判断;
02
知识精讲
(二)判断直线y=kx+b(k≠0)与抛物线y=ax2+bx+c(a≠0)的交点个数:
(1)当>0时,两个不同的实数根→直线与抛物线有两个不同的交点,
(2)当=0时,两个相同的实数根→直线与抛物线有一个交点,
(3)当<0时,没有实数根→直线与抛物线没有交点。
例1、抛物线与直线y=m有交点,图中抛物线的表达式为y=ax +bx+c,根据图像判断下列方程根的情况。
(1)方程ax +bx+c=0的两根分别为__________________;
(2)方程ax +bx+c-3=0的两根分别为__________________;
(3)方程ax +bx+c=2的根的情况是__________________;
(4)方程ax +bx+c=4的根的情况是__________________。
x1=-2.5,x2=0.5
可以看作:抛物线y=ax +bx+c与直线y=3联立所得,
故方程的两根=抛物线y=ax +bx+c与直线y=3交点的横坐标。
x1=-1,x2=-1
03
典例精析
例1、抛物线与直线y=m有交点,图中抛物线的表达式为y=ax +bx+c,根据图像判断下列方程根的情况。
(1)方程ax +bx+c=0的两根分别为__________________;
(2)方程ax +bx+c-3=0的两根分别为__________________;
(3)方程ax +bx+c=2的根的情况是__________________;
(4)方程ax +bx+c=4的根的情况是__________________。
可以看作:抛物线y=ax +bx+c与直线y=2联立所得,
故方程的根的情况需分析抛物线y=ax +bx+c与直线y=2的交点情况。
03
典例精析
有两个不同的实数根
x1=-2.5,x2=0.5
x1=-1,x2=-1
例1、抛物线与直线y=m有交点,图中抛物线的表达式为y=ax +bx+c,根据图像判断下列方程根的情况。
(1)方程ax +bx+c=0的两根分别为__________________;
(2)方程ax +bx+c-3=0的两根分别为__________________;
(3)方程ax +bx+c=2的根的情况是__________________;
(4)方程ax +bx+c=4的根的情况是__________________。
可以看作:抛物线y=ax +bx+c与直线y=4联立所得,
故方程的根的情况需分析抛物线y=ax +bx+c与直线y=4的交点情况。
03
典例精析
有两个不同的实数根
x1=-2.5,x2=0.5
x1=-1,x2=-1
没有实数根
例2、(1)求直线y=x+1与抛物线y=x2-1的交点坐标;
(2)求直线y=2x-6与抛物线y=2x -6x+4的交点坐标。
解:(1)联立,得:x2-1=x+1,
即x2-x-2=0,(x+1)(x-2)=0,
解得:x=-1或x=2,则直线与抛物线的交点坐标为(-1,0),(2,3);
03
典例精析
例2、(1)求直线y=x+1与抛物线y=x2-1的交点坐标;
(2)求直线y=2x-6与抛物线y=2x -6x+4的交点坐标。
(2)联立,得:2x -6x+4=2x-6,即x2-4x+5=0,
∵=16-20<0,
∴直线与抛物线无交点。
03
典例精析
例3、已知a,b是关于x的方程(x-a)(x-b)=2的两个根,其中a
可以看作:
抛物线y=(x-a)(x-b)与直线y=2联立所得
03
典例精析
课后总结
y=ax2+bx+c(a≠0)的图像与x轴有两个交点
y=ax2+bx+c(a≠0)的图像与x轴有一个交点
y=ax2+bx+c(a≠0)的图像与x轴有没有交点
ax2+bx+c=0(a≠0)有两个不同的实数根
ax2+bx+c=0(a≠0)有两个相同的实数根
ax2+bx+c=0(a≠0)没有实数根
=b2-4ac>0
=b2-4ac=0
=b2-4ac<0
y=ax2+bx+c(a≠0)的图像与x轴交点的横坐标=ax2+bx+c=0(a≠0)的解
图像法确定一元二次方程的根的情况:
课后总结
直线与抛物线的交点问题:
(一)交点坐标
联立,得一元二次方程:ax2+(b-k)x+c-b=0,
在方程有解的情况下,解一元二次方程得:交点的横坐标,
将横坐标代入直线方程得:交点的纵坐标。
(二)交点个数
交点个数可通过联立所得的一元二次方程的根的情况判断:
(1)当>0时,两个不同的实数根→直线与抛物线有两个不同的交点,
(2)当=0时,两个相同的实数根→直线与抛物线有一个交点,
(3)当<0时,没有实数根→直线与抛物线没有交点。
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
