19.8直角三角形性质(第2课时) 课件(共30张PPT)-2023-2024学年八年级数学上册同步精品课堂(沪教版)
文档属性
| 名称 | 19.8直角三角形性质(第2课时) 课件(共30张PPT)-2023-2024学年八年级数学上册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 06:02:32 | ||
图片预览









文档简介
(共30张PPT)
沪教版八年级上册
第 19 章 几何证明
19.8直角三角形性质(第2课时)
学习目标
1.通过探索含有30°锐角的直角三角形的图形,猜想、发现、归纳出30°所对的直角边与斜边之间的关系;
2.经历直角三角形性质定理的两条推论的探索过程,掌握直角三角形性质定理的两条重要推论及推导;
3.初步学会运用直角三角形性质定理的两条重要推论来进行简单的几何证明。
问题引入
问题1 如图,将两个相同的含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
分离
拼接
A
C
B
问题2 将一张等边三角形纸片,沿一边上的高对折,如图所示,你有什么发现?
含30°角的直角三角形的性质
性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
B
C
D
如图,△ADC是△ABC的轴对称图形,
因此AB=AD, ∠BAD=2×30°=60°,
从而△ABD是一个等边三角形.
再由AC⊥BD,
可得BC=CD= AB.
你还能用其他方法证明吗?
已知:如图,在Rt△ABC中,∠C=90°,∠BAC=30°
证明:延长BC至D,使CD=BC,连结AD.
1
2
求证:BC= AB
B
C
)
30°
A
D
∴ △ABC≌△ADC(SAS)
在△ABC与△ADC中
∴AB=AD
又∵ △ABC 是等边三角形
BC=DC
∠ACB=∠ACD
AC=AC
∴BC=DC= BD= AB
1
2
1
2
D
B
C
A
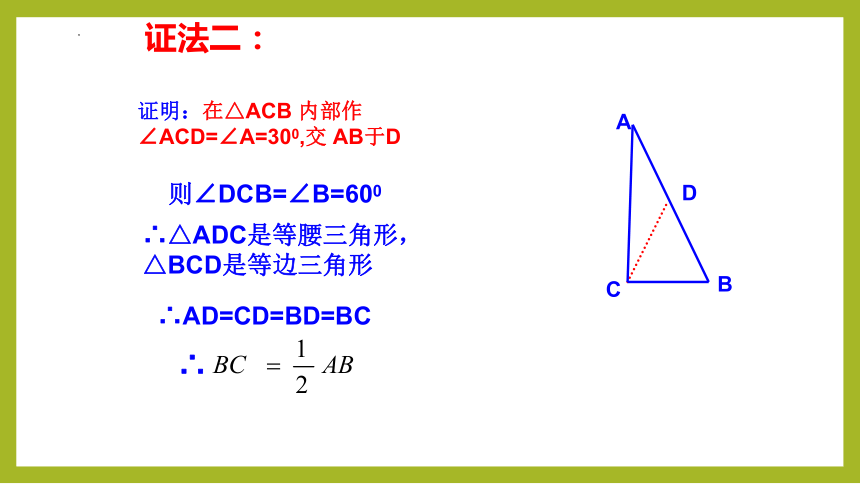
证明:在△ACB 内部作 ∠ACD=∠A=300,交 AB于D
∴△ADC是等腰三角形,
△BCD是等边三角形
则∠DCB=∠B=600
∴AD=CD=BD=BC
∴
证法二:
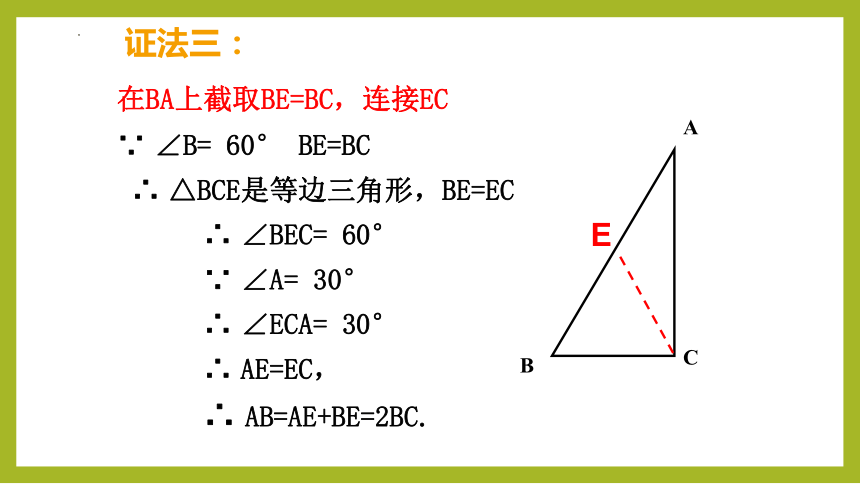
在BA上截取BE=BC,连接EC
∵ ∠B= 60° BE=BC
∴ △BCE是等边三角形,BE=EC
∴ ∠BEC= 60°
∵ ∠A= 30°
∴ ∠ECA= 30°
∴ AE=EC,
∴ AB=AE+BE=2BC.
E
A
C
B
证法三:
E
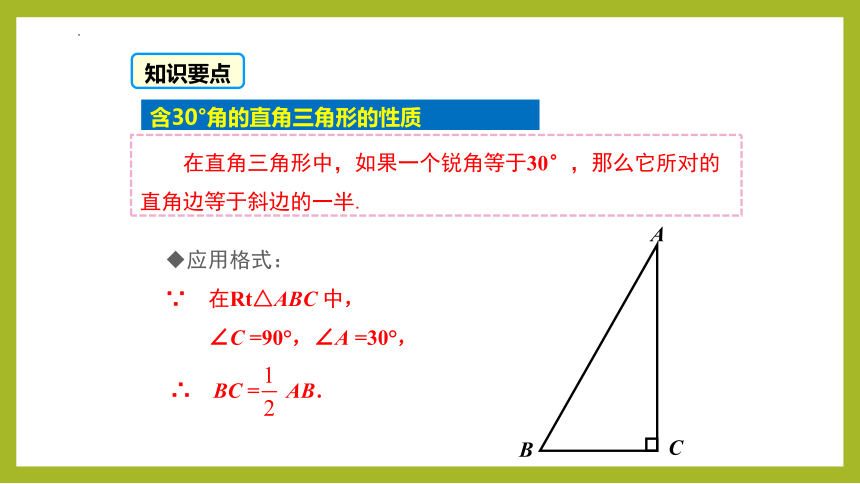
知识要点
含30°角的直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
应用格式:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°,
A
B
C
∴ BC = AB.
推论:由定理直接推出来的定理叫做推论.
以上命题的证明,是从直角三角形的性质定理2推出来的定理,把它称为直角三角形性质定理2的推论.
推论1:在直角三角形中,如果有一个锐角等于
30 ,那么它所对的直角边等于斜边的一半.
逆命题:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30 .
a
2a
30°
BC= AB
CD= AB
BD= AB
逆命题:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30 .
已知:如图,在Rt△ABC中,∠ACB=90 ,BC= AB.
求证:∠A=30 .
D
分析
做斜边AB上的中线CD,
构造出等边△BCD
得∠B=60 ,从而得∠A=30 .
是真命题吗?
是真命题
60
推论2:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30 .
a
2a
30°
例题 3 已知:如图,在△ABC中,AB=AC,
∠B=30 ,AD⊥AC.
求证:BD= CD.
30°
30°
60°
AD=BD,从而BD= CD.
30°
Rt △ADC中, ∠C =30 得AD= CD.
AB=AC, ∠B=30 , 可得到∠C =30 .
分析
例题 3 已知:如图,在△ABC中,AB=AC,
∠B=30 ,AD⊥AC.
求证:BD= CD.
证明:
例题4 如图,在Rt△ABC中,∠ACB=90 ,CD⊥AB,
点D为垂足,CE是斜边AB边上的中线,且ED=BD.
求证:∠A=30 .
根据推论2得: ∠A=30
例题4 如图,在Rt△ABC中,∠ACB=90 ,CD⊥AB,
点D为垂足,CE是斜边AB边上的中线,且ED=BD.
求证:∠A=30 .
证明:
图中,与CE相等的线段有哪些?
CE=CB=AE=EB
若AB=8,则DB=
课本练习
1.已知:如图,在△ABC 中,∠BAC=120°,AB=AC,AB 边上的垂直平分线交 BC于点D,交 AB 于点E,联结 AD.求证:CD=2BD.
提示:先推出∠B=∠C=30°.然后证∠DAC=90°,得到CD=2AD.再推出CD=2BD.
2.如图,已知△ABC中,AB=AC,点 D在BC 边上,∠DAC=90°,AD=CD.
求∠BAC的度数.
【答案】 ∠BAC=120°
1.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米
C.12米 D.15米
2.某市在旧城改造中,计划在一块如图所示的△ABC空地上种植草皮以美化环境,已知∠A=150°,这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A.300a元 B.150a元
C.450a元 D.225a元
B
B
随堂检测
4.在△ABC中,∠A: ∠B: ∠C=1:2:3,若AB=10,则BC
= .
5
5.如图,Rt△ABC中,∠C= 90°,∠A= 30°,AB+BC=12 cm,则AB=________.
A
C
B
8 cm
3.如图,在△ABC 中,∠ACB =90°,CD 是高,∠A =30°,AB =4.则BD = .
A
B
C
D
1
第3题图
第5题图
6.已知:等腰三角形的底角为150,腰长为20.
求:腰上的高.
∵∠B=∠ACB=150(已知),
∴∠DAC=∠B+∠ACB= 150+150=300
∴CD= AC= ×20=10
A
C
B
D
150
150
20
解:过C作CD⊥BA交BA的延长线于点D
7.如图,在△ABC中,∠C=90°,∠B=15°,DE是AB的垂直平分线,BE=5,则求AC的长.
解:连接AE,
∵DE是AB的垂直平分线,
∴BE=AE,
∴∠EAB=∠B=15°,
∴∠AEC=∠EAB+∠B=30°.
∵∠C=90°,
∴AC= AE= BE=2.5.
8.如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°,然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13 m,求旗杆AB的高度.
A
B
C
D
解: ∵∠ACB=15°,∠ADB=30°,
∴∠CAD=∠ADB-∠ACB=30°-15°=15°,
∴∠ACB=∠CAD,∴AD=CD=13 m.
在△ADB中,
∵AB⊥DB,∠ADB=30°,
9.如图,△ABC中,∠C=90°,∠A=60 °,EF是AB的垂直平分线,判断CE与BE之间的关系
解:结论:CE= BE,连接AE
∵∠C=90°,∠A=60 °∴∠B=30°
∵EF是AB的垂直平分线,∴BE=AE
∴∠B=∠BAE=30°
∴∠BAE=30°
∴CE= AE
∴CE= BE
10.如图,在△ABC中 ,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于E点,求证:BE=3EA.
证明:∵AB=AC,∠BAC=120°, ∴∠B=∠C=30°.
∵ D是BC的中点,∴AD⊥BC.
∴∠ADB=90°,∠BAD=∠DAC=60°.
∴AB=2AD.
∵DE⊥AB,∴∠AED=90°,
∴∠ADE=30°,∴AD=2AE.
∴AB=4AE,∴BE=3AE.
11.如图,已知△ABC是等边三角形,D,E分别为BC、AC上的点,且CD=AE,AD、BE相交于点P,BQ⊥AD于点Q.求证:BP=2PQ.
∴△ADC≌△BEA.
证明:∵△ABC为等边三角形,
∴ AC=BC=AB ,∠C=∠BAC=60°.
∵CD=AE,
∴∠CAD=∠ABE.
∵∠BAP+∠CAD=60°,
∴∠ABE+∠BAP=60°.
∴∠BPQ=60°.
又∵ BQ⊥AD,
∴BP=2PQ.
∴∠PBQ=30°,
∴∠BQP=90°,
推论1:在直角三角形中,如果有一个锐角等于
30 ,那么它所对的直角边等于斜边的一半.
a
2a
30°
课堂小结
推论2:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30 .
a
2a
30°
a
2a
30°
2a
a
30°
a
30°
2a
∠A=30°
a
2a
a
2a
30°
2a
30°
2a
30°
2a
AB=2BC
沪教版八年级上册
第 19 章 几何证明
19.8直角三角形性质(第2课时)
学习目标
1.通过探索含有30°锐角的直角三角形的图形,猜想、发现、归纳出30°所对的直角边与斜边之间的关系;
2.经历直角三角形性质定理的两条推论的探索过程,掌握直角三角形性质定理的两条重要推论及推导;
3.初步学会运用直角三角形性质定理的两条重要推论来进行简单的几何证明。
问题引入
问题1 如图,将两个相同的含30°角的三角尺摆放在一起,你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
分离
拼接
A
C
B
问题2 将一张等边三角形纸片,沿一边上的高对折,如图所示,你有什么发现?
含30°角的直角三角形的性质
性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
B
C
D
如图,△ADC是△ABC的轴对称图形,
因此AB=AD, ∠BAD=2×30°=60°,
从而△ABD是一个等边三角形.
再由AC⊥BD,
可得BC=CD= AB.
你还能用其他方法证明吗?
已知:如图,在Rt△ABC中,∠C=90°,∠BAC=30°
证明:延长BC至D,使CD=BC,连结AD.
1
2
求证:BC= AB
B
C
)
30°
A
D
∴ △ABC≌△ADC(SAS)
在△ABC与△ADC中
∴AB=AD
又∵ △ABC 是等边三角形
BC=DC
∠ACB=∠ACD
AC=AC
∴BC=DC= BD= AB
1
2
1
2
D
B
C
A
证明:在△ACB 内部作 ∠ACD=∠A=300,交 AB于D
∴△ADC是等腰三角形,
△BCD是等边三角形
则∠DCB=∠B=600
∴AD=CD=BD=BC
∴
证法二:
在BA上截取BE=BC,连接EC
∵ ∠B= 60° BE=BC
∴ △BCE是等边三角形,BE=EC
∴ ∠BEC= 60°
∵ ∠A= 30°
∴ ∠ECA= 30°
∴ AE=EC,
∴ AB=AE+BE=2BC.
E
A
C
B
证法三:
E
知识要点
含30°角的直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
应用格式:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°,
A
B
C
∴ BC = AB.
推论:由定理直接推出来的定理叫做推论.
以上命题的证明,是从直角三角形的性质定理2推出来的定理,把它称为直角三角形性质定理2的推论.
推论1:在直角三角形中,如果有一个锐角等于
30 ,那么它所对的直角边等于斜边的一半.
逆命题:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30 .
a
2a
30°
BC= AB
CD= AB
BD= AB
逆命题:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30 .
已知:如图,在Rt△ABC中,∠ACB=90 ,BC= AB.
求证:∠A=30 .
D
分析
做斜边AB上的中线CD,
构造出等边△BCD
得∠B=60 ,从而得∠A=30 .
是真命题吗?
是真命题
60
推论2:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30 .
a
2a
30°
例题 3 已知:如图,在△ABC中,AB=AC,
∠B=30 ,AD⊥AC.
求证:BD= CD.
30°
30°
60°
AD=BD,从而BD= CD.
30°
Rt △ADC中, ∠C =30 得AD= CD.
AB=AC, ∠B=30 , 可得到∠C =30 .
分析
例题 3 已知:如图,在△ABC中,AB=AC,
∠B=30 ,AD⊥AC.
求证:BD= CD.
证明:
例题4 如图,在Rt△ABC中,∠ACB=90 ,CD⊥AB,
点D为垂足,CE是斜边AB边上的中线,且ED=BD.
求证:∠A=30 .
根据推论2得: ∠A=30
例题4 如图,在Rt△ABC中,∠ACB=90 ,CD⊥AB,
点D为垂足,CE是斜边AB边上的中线,且ED=BD.
求证:∠A=30 .
证明:
图中,与CE相等的线段有哪些?
CE=CB=AE=EB
若AB=8,则DB=
课本练习
1.已知:如图,在△ABC 中,∠BAC=120°,AB=AC,AB 边上的垂直平分线交 BC于点D,交 AB 于点E,联结 AD.求证:CD=2BD.
提示:先推出∠B=∠C=30°.然后证∠DAC=90°,得到CD=2AD.再推出CD=2BD.
2.如图,已知△ABC中,AB=AC,点 D在BC 边上,∠DAC=90°,AD=CD.
求∠BAC的度数.
【答案】 ∠BAC=120°
1.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米
C.12米 D.15米
2.某市在旧城改造中,计划在一块如图所示的△ABC空地上种植草皮以美化环境,已知∠A=150°,这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A.300a元 B.150a元
C.450a元 D.225a元
B
B
随堂检测
4.在△ABC中,∠A: ∠B: ∠C=1:2:3,若AB=10,则BC
= .
5
5.如图,Rt△ABC中,∠C= 90°,∠A= 30°,AB+BC=12 cm,则AB=________.
A
C
B
8 cm
3.如图,在△ABC 中,∠ACB =90°,CD 是高,∠A =30°,AB =4.则BD = .
A
B
C
D
1
第3题图
第5题图
6.已知:等腰三角形的底角为150,腰长为20.
求:腰上的高.
∵∠B=∠ACB=150(已知),
∴∠DAC=∠B+∠ACB= 150+150=300
∴CD= AC= ×20=10
A
C
B
D
150
150
20
解:过C作CD⊥BA交BA的延长线于点D
7.如图,在△ABC中,∠C=90°,∠B=15°,DE是AB的垂直平分线,BE=5,则求AC的长.
解:连接AE,
∵DE是AB的垂直平分线,
∴BE=AE,
∴∠EAB=∠B=15°,
∴∠AEC=∠EAB+∠B=30°.
∵∠C=90°,
∴AC= AE= BE=2.5.
8.如图,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°,然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13 m,求旗杆AB的高度.
A
B
C
D
解: ∵∠ACB=15°,∠ADB=30°,
∴∠CAD=∠ADB-∠ACB=30°-15°=15°,
∴∠ACB=∠CAD,∴AD=CD=13 m.
在△ADB中,
∵AB⊥DB,∠ADB=30°,
9.如图,△ABC中,∠C=90°,∠A=60 °,EF是AB的垂直平分线,判断CE与BE之间的关系
解:结论:CE= BE,连接AE
∵∠C=90°,∠A=60 °∴∠B=30°
∵EF是AB的垂直平分线,∴BE=AE
∴∠B=∠BAE=30°
∴∠BAE=30°
∴CE= AE
∴CE= BE
10.如图,在△ABC中 ,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于E点,求证:BE=3EA.
证明:∵AB=AC,∠BAC=120°, ∴∠B=∠C=30°.
∵ D是BC的中点,∴AD⊥BC.
∴∠ADB=90°,∠BAD=∠DAC=60°.
∴AB=2AD.
∵DE⊥AB,∴∠AED=90°,
∴∠ADE=30°,∴AD=2AE.
∴AB=4AE,∴BE=3AE.
11.如图,已知△ABC是等边三角形,D,E分别为BC、AC上的点,且CD=AE,AD、BE相交于点P,BQ⊥AD于点Q.求证:BP=2PQ.
∴△ADC≌△BEA.
证明:∵△ABC为等边三角形,
∴ AC=BC=AB ,∠C=∠BAC=60°.
∵CD=AE,
∴∠CAD=∠ABE.
∵∠BAP+∠CAD=60°,
∴∠ABE+∠BAP=60°.
∴∠BPQ=60°.
又∵ BQ⊥AD,
∴BP=2PQ.
∴∠PBQ=30°,
∴∠BQP=90°,
推论1:在直角三角形中,如果有一个锐角等于
30 ,那么它所对的直角边等于斜边的一半.
a
2a
30°
课堂小结
推论2:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30 .
a
2a
30°
a
2a
30°
2a
a
30°
a
30°
2a
∠A=30°
a
2a
a
2a
30°
2a
30°
2a
30°
2a
AB=2BC
