19.8直角三角形性质(第1课时) 课件(共20张PPT)-2023-2024学年八年级数学上册同步精品课堂(沪教版)
文档属性
| 名称 | 19.8直角三角形性质(第1课时) 课件(共20张PPT)-2023-2024学年八年级数学上册同步精品课堂(沪教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 919.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 06:01:28 | ||
图片预览







文档简介
(共20张PPT)
沪教版八年级上册
第 19 章 几何证明
19.8直角三角形性质(第1课时)
学习目标
1.掌握直角三角形的两个锐角互余的定理及运用;
2.经历推导证明直角三角形斜边上的中线等于斜边的一半的过程中体会从特殊到一般的研究问题的方法;
3.掌握直角三角形斜边上的中线等于斜边的一半的定理及运用。
复习:
(1)什么叫直角三角形?
(2)直角三角形是一类特殊的三角形,除了具备三角形的性质外,还具备哪些性质?
有一个角是直角的三角形叫直角三角形
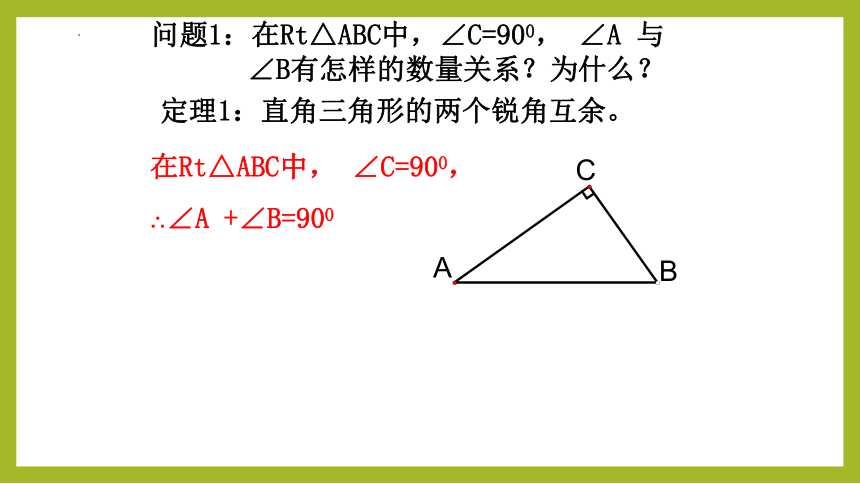
问题1:在Rt△ABC中,∠C=900, ∠A 与∠B有怎样的数量关系?为什么?
定理1:直角三角形的两个锐角互余。
在Rt△ABC中, ∠C=900,
∴∠A +∠B=900
思考:如图,在Rt△ABC,∠ACB=900, CD是斜边AB上的中线,猜测一下刚刚得到的命题
直角三角形斜边上的中线等于斜边的一半
还成立吗?
例1.已知:在Rt△ABC中, ACB=90°,CD是斜边AB上的中线。
求证:CD= AB
证明:延长CD到C’,使C’D=CD,连接AC’
A
C
B
C’
D
∴AC’=BC , C’AD= B
{
在△ADC’与△BDC中
AD=BD (已知)
ADC’= BDC(对顶角相等)
C’D=CD (已作)
∴ △ADC’ ≌ △BDC (SAS)
∵ BCA=90° ∴ BAC+ B=90°
∴ BAC+ C’AD=90° ∴ CAC’= ACB
在△ACC’与△ACB中
AC’=BC (已证)
CAC’= ACB (已证)
AC=AC (公共边)
∴ △ACC’ ≌ △ACB (SAS)
{
∴AB= CC’ 又CD= CC’
∴CD= AB
定理2
直角三角形斜边上的中线等于斜边的一半。
符号语言表示:
∵∠ACB=90°,CD是斜边AB上的中线或点D是AB的中点(已知),
∴CD=AD=BD= AB(直角三角形斜边上的中线等于斜边的一半).
已知:在Rt△ABC中, ACB=90°,
CD斜边上AB的中线。
巩固练习2
(1)如果AB=8,那么CD=
(2)如果CD=8,那么AB=
(3)如果∠A=250,那么∠CDB=
4
16
500
例题2:已知:如图,在⊿ABC,AD⊥BC,E、F
分别是AB、AC的中点,且DE=DF
求证:AB=AC
B
C
A
D
E
F
解 ∵AD ⊥BC
∵ E、F分别是AB,AC的中点。
∴DE= AB , DF= AC
( )
直角三角形斜边上的中线等于斜边的一半
又∵AB=AC
∴DE=DF
∴∠ADB= ∠ADC=900(垂直的意义)
1.如图,已知 D为AB 的中点,EA⊥AB,CB⊥AB,AE=AB=2BC,那么下列结论中不正确的是( )
DE=AC; (B)∠E+∠C=90°;
(C) ∠CAB=30° ; (D)∠EAF=∠ADE
课本练习
2.已知:如图,BD、CE分别是△ABC的高,M、N分别是 BC、DE的中点,分别联结ME、MD.求证:MN⊥ED.
证明:∵BD、CE是ABC的两条高.
∴∠BEC =∠BDC =90°
∵BM =MC.
∴EM = DM
∵N是DE的中点
∴MN⊥DE
3.如图,△ABC中,∠ABC=90°,E为AC 的中点.在图中作点 D,使AD∥BE,∠ADC=90°;在AD上取点F,使FD=BE;分别联结 EF、ED、BD试判断EF与BD之间具有怎样的位置关系.
证明:EF⊥BD连接BF
∵BE∥DF,BE=DF
∴四边形BEDF是平行四边形·
∵∠ADC =∠ABC =90°,E为AC的中点,
∴四边形BEDF是菱形
∴DF与BD互相垂直平分
证明:取DE中点F连接AF
AF=DF (直角三角形斜边中线等于斜边一半)
所以∠FAD=∠D
∠AFE=∠D+∠FAD=2∠D
所以,∠ABE= ∠AFE
所以AF=AB
因为DE=2AF
所以ED = 2AB
1.如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.
90°
2.如图,AB、CD相交于点O,AC⊥CD于点C,
若∠BOD=38°,则∠A=________.
52°
第1题图
第2题图
3.在△ABC中,若∠A=43°,∠B=47°,则这个三角形是____________.
直角三角形
随堂检测
4.在一个直角三角形中,有一个锐角等于40°,则另
一个锐角的度数是( )
A.40° B.50° C.60° D.70°
B
5.具备下列条件的△ABC中,不是直角三角形的是
( )
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
D
6.如图所示,△ABC为直角三角形,∠ACB=90°,
CD⊥AB,与∠1互余的角有( )
A.∠B B.∠A
C.∠BCD和∠A D.∠BCD
C
7.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.求证:△ACD是直角三角形.
证明:∵∠ACB=90°,
∴∠A+∠B=90°.
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.
8. Rt△ABC中,∠ACB=90 °,∠A=30°,求证:BC= AB.
A
B
C
┐
D
证明:作斜边上的中线CD,
则CD=AD=BD= AB
(在直角三角形中,斜边上的中线等于斜边的一半)
∵ ∠A=30°
∴ ∠B=60°
∴ △CDB是等边三角形,
∴ BC=BD= AB
对此,你能得出什么结论?
30°
9.如图,在△ABC中,∠B=∠C,D、E分别是BC、AC的中点,AB=6,求DE的长。
解:∵∠B=∠C
∴AB=AC=6
∵D是BC的中点
∴AD⊥BC
∵E是AC的中点
∴DE= AC=3
直角三角形的性质
1.直角三角形的两个锐角互余,两条直角边的平方和等于斜边的平方。
2.直角三角形斜边上的中线等于斜边的一半.
课堂小结
沪教版八年级上册
第 19 章 几何证明
19.8直角三角形性质(第1课时)
学习目标
1.掌握直角三角形的两个锐角互余的定理及运用;
2.经历推导证明直角三角形斜边上的中线等于斜边的一半的过程中体会从特殊到一般的研究问题的方法;
3.掌握直角三角形斜边上的中线等于斜边的一半的定理及运用。
复习:
(1)什么叫直角三角形?
(2)直角三角形是一类特殊的三角形,除了具备三角形的性质外,还具备哪些性质?
有一个角是直角的三角形叫直角三角形
问题1:在Rt△ABC中,∠C=900, ∠A 与∠B有怎样的数量关系?为什么?
定理1:直角三角形的两个锐角互余。
在Rt△ABC中, ∠C=900,
∴∠A +∠B=900
思考:如图,在Rt△ABC,∠ACB=900, CD是斜边AB上的中线,猜测一下刚刚得到的命题
直角三角形斜边上的中线等于斜边的一半
还成立吗?
例1.已知:在Rt△ABC中, ACB=90°,CD是斜边AB上的中线。
求证:CD= AB
证明:延长CD到C’,使C’D=CD,连接AC’
A
C
B
C’
D
∴AC’=BC , C’AD= B
{
在△ADC’与△BDC中
AD=BD (已知)
ADC’= BDC(对顶角相等)
C’D=CD (已作)
∴ △ADC’ ≌ △BDC (SAS)
∵ BCA=90° ∴ BAC+ B=90°
∴ BAC+ C’AD=90° ∴ CAC’= ACB
在△ACC’与△ACB中
AC’=BC (已证)
CAC’= ACB (已证)
AC=AC (公共边)
∴ △ACC’ ≌ △ACB (SAS)
{
∴AB= CC’ 又CD= CC’
∴CD= AB
定理2
直角三角形斜边上的中线等于斜边的一半。
符号语言表示:
∵∠ACB=90°,CD是斜边AB上的中线或点D是AB的中点(已知),
∴CD=AD=BD= AB(直角三角形斜边上的中线等于斜边的一半).
已知:在Rt△ABC中, ACB=90°,
CD斜边上AB的中线。
巩固练习2
(1)如果AB=8,那么CD=
(2)如果CD=8,那么AB=
(3)如果∠A=250,那么∠CDB=
4
16
500
例题2:已知:如图,在⊿ABC,AD⊥BC,E、F
分别是AB、AC的中点,且DE=DF
求证:AB=AC
B
C
A
D
E
F
解 ∵AD ⊥BC
∵ E、F分别是AB,AC的中点。
∴DE= AB , DF= AC
( )
直角三角形斜边上的中线等于斜边的一半
又∵AB=AC
∴DE=DF
∴∠ADB= ∠ADC=900(垂直的意义)
1.如图,已知 D为AB 的中点,EA⊥AB,CB⊥AB,AE=AB=2BC,那么下列结论中不正确的是( )
DE=AC; (B)∠E+∠C=90°;
(C) ∠CAB=30° ; (D)∠EAF=∠ADE
课本练习
2.已知:如图,BD、CE分别是△ABC的高,M、N分别是 BC、DE的中点,分别联结ME、MD.求证:MN⊥ED.
证明:∵BD、CE是ABC的两条高.
∴∠BEC =∠BDC =90°
∵BM =MC.
∴EM = DM
∵N是DE的中点
∴MN⊥DE
3.如图,△ABC中,∠ABC=90°,E为AC 的中点.在图中作点 D,使AD∥BE,∠ADC=90°;在AD上取点F,使FD=BE;分别联结 EF、ED、BD试判断EF与BD之间具有怎样的位置关系.
证明:EF⊥BD连接BF
∵BE∥DF,BE=DF
∴四边形BEDF是平行四边形·
∵∠ADC =∠ABC =90°,E为AC的中点,
∴四边形BEDF是菱形
∴DF与BD互相垂直平分
证明:取DE中点F连接AF
AF=DF (直角三角形斜边中线等于斜边一半)
所以∠FAD=∠D
∠AFE=∠D+∠FAD=2∠D
所以,∠ABE= ∠AFE
所以AF=AB
因为DE=2AF
所以ED = 2AB
1.如图,一张长方形纸片,剪去一部分后得到一个三角形,则图中∠1+∠2的度数是________.
90°
2.如图,AB、CD相交于点O,AC⊥CD于点C,
若∠BOD=38°,则∠A=________.
52°
第1题图
第2题图
3.在△ABC中,若∠A=43°,∠B=47°,则这个三角形是____________.
直角三角形
随堂检测
4.在一个直角三角形中,有一个锐角等于40°,则另
一个锐角的度数是( )
A.40° B.50° C.60° D.70°
B
5.具备下列条件的△ABC中,不是直角三角形的是
( )
A.∠A+∠B=∠C
B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3
D.∠A=∠B=3∠C
D
6.如图所示,△ABC为直角三角形,∠ACB=90°,
CD⊥AB,与∠1互余的角有( )
A.∠B B.∠A
C.∠BCD和∠A D.∠BCD
C
7.如图,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.求证:△ACD是直角三角形.
证明:∵∠ACB=90°,
∴∠A+∠B=90°.
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴△ACD是直角三角形.
8. Rt△ABC中,∠ACB=90 °,∠A=30°,求证:BC= AB.
A
B
C
┐
D
证明:作斜边上的中线CD,
则CD=AD=BD= AB
(在直角三角形中,斜边上的中线等于斜边的一半)
∵ ∠A=30°
∴ ∠B=60°
∴ △CDB是等边三角形,
∴ BC=BD= AB
对此,你能得出什么结论?
30°
9.如图,在△ABC中,∠B=∠C,D、E分别是BC、AC的中点,AB=6,求DE的长。
解:∵∠B=∠C
∴AB=AC=6
∵D是BC的中点
∴AD⊥BC
∵E是AC的中点
∴DE= AC=3
直角三角形的性质
1.直角三角形的两个锐角互余,两条直角边的平方和等于斜边的平方。
2.直角三角形斜边上的中线等于斜边的一半.
课堂小结
