七年级数学下册第八章整章水平测试(A)
文档属性
| 名称 | 七年级数学下册第八章整章水平测试(A) |

|
|
| 格式 | rar | ||
| 文件大小 | 72.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 五四学制版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-10 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
七年级数学下册第八章整章水平测试(A)
一、试试你的身手(每小题3分,共24分)
1.由同一张底片冲洗出来的两张五寸照片的图案 全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片 全等图形(填“是”或“不是”).
2.中,和的平分线相交于点,若,则的度数为 .
3.“两个锐角对应相等” (填“能”或“不能”)判别两个直角三角形相等.
4.如图1,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B=20°,则∠C= .
5.在平面中,到一个三角形三边的距离相等的点共有 个,到一个三角形三边所在直线的距离相等的点有 个.
6.在△ABC中,∠C=90°,AD为△ABC角平分线,BC=40,AB=50,若BD∶DC=5∶ 3,则△ADB的面积为 .
7.如图2,∠ACB=∠DBC,要想说明△ABC≌△DCB,只需增加的一个条件是 .(只需填一个你认为合适的条件)
8.如图3,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=36cm2,AB=18cm,BC=12cm,则DE= cm.
二、相信你的选择(每小题3分,共24分)
1.下列说法:
(1)只有两个三角形才能完全重合;
(2)如果两个图形全等,它们的形状和大小一定都相同;
(3)两个正方形一定是全等形;
(4)边数相同的图形一定能互相重合.
其中错误说法的为( )
A.(1)(3) B.(1)(2)(3) C.(1)(3)(4) D.(1)(4)
2.如图4所示,△ABC≌△EDF,F、C在AE上,DF=BC,AB=ED,AE=20,FC=10, 则AC的长为( )
A.10 B.5 C.15 D.20
3.△ABC中,∠A=∠B,若与△ABC全等的三角形中有一个角为120°,则△ABC中等于120°的角为( )
A.∠A B.∠B C.∠C D.∠A或∠C
4.如图5,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE;(2)BC=EF;(3)AC=DF ;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F,以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )
A.(1)(5)(2) B.(1)(2)(3) C.(4)(6)(1) D.(2)(3)(4)
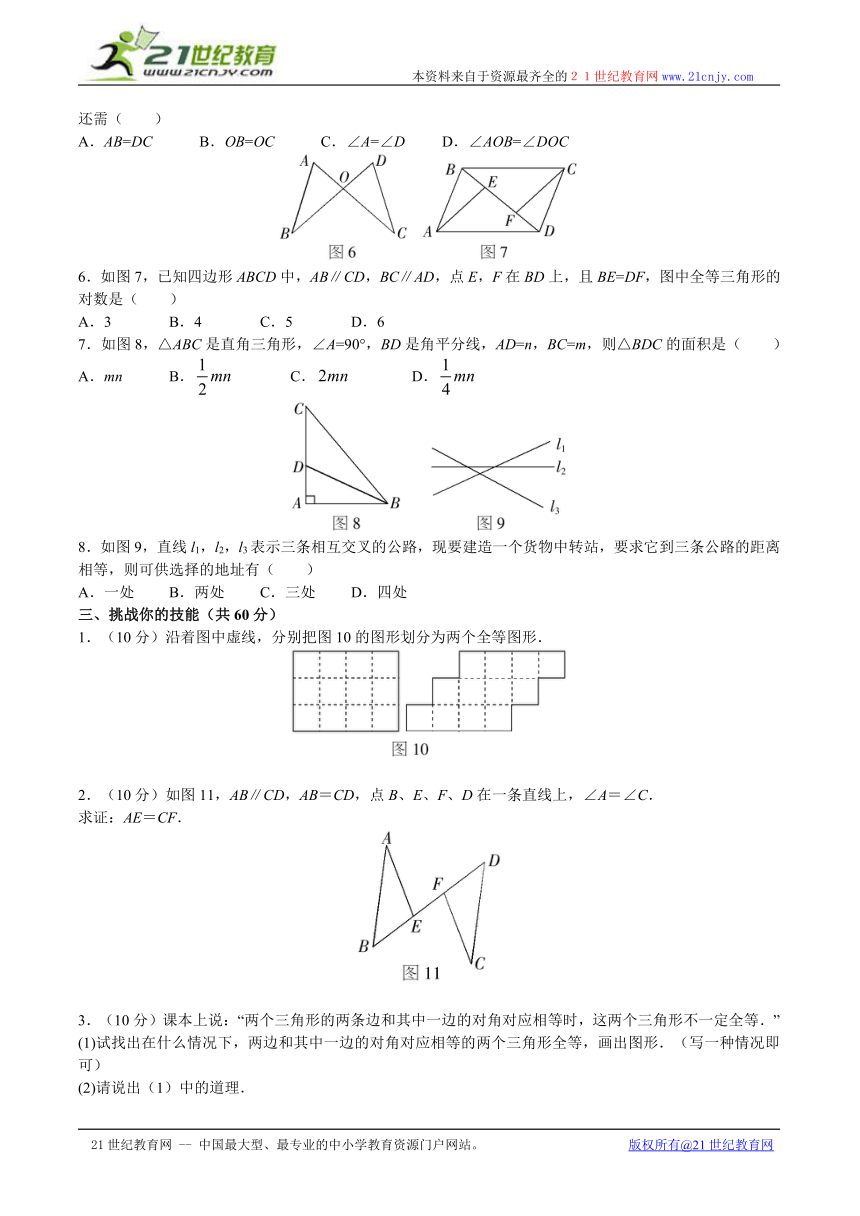
5.如图6,AC和BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )
A.AB=DC B.OB=OC C.∠A=∠D D.∠AOB=∠DOC
6.如图7,已知四边形ABCD中,AB∥CD,BC∥AD,点E,F在BD上,且BE=DF,图中全等三角形的对数是( )
A.3 B.4 C.5 D.6
7.如图8,△ABC是直角三角形,∠A=90°,BD是角平分线,AD=n,BC=m,则△BDC的面积是( )
A.mn B. C. D.
8.如图9,直线l1,l2,l3表示三条相互交叉的公路,现要建造一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B.两处 C.三处 D.四处
三、挑战你的技能(共60分)
1.(10分)沿着图中虚线,分别把图10的图形划分为两个全等图形.
2.(10分)如图11,AB∥CD,AB=CD,点B、E、F、D在一条直线上,∠A=∠C.
求证:AE=CF.
3.(10分)课本上说:“两个三角形的两条边和其中一边的对角对应相等时,这两个三角形不一定全等.”
(1)试找出在什么情况下,两边和其中一边的对角对应相等的两个三角形全等,画出图形.(写一种情况即可)
(2)请说出(1)中的道理.
4.(10分)如图12,△ABC中,∠ABC=45°,AD⊥BC于D,点E在AD上,且DE=CD.
求证:BE=AC.
5.(10分)已知,如图13,PB、PC分别是△ABC的外角平分线,且相交于点P.
求证:点P在∠A的平分线上.
6.(10分)如图14,四边形ABCD中,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD的延长线于F,图中有无和△ABE全等的三角形,请说明理由.
四、拓广探索(本题12分)
如图15(1),E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.
(1)求证:MB=MD,ME=MF;
(2)当E、F两点移动至如图15(2)所示的位置时,其余条件不变,上述结论是否成立?若成立,请加以证明.
参考答案:
一、1.是,不是 2. 3.不能 4. 5.1,4
6.375 7.或或(答案不惟一) 8.2.4
二、1~4.CCCD 5~8.BABD
三、1.略
2.证明略
3.(1)答案不惟一,现举一例,在两三角形都是直角三角形时成立,图略
(2)根据判定两个直角三角形全等的条件当,时,
由“HL”得
4.证明略
5.证明略
6.有,为,理由略
四、(1)证明略
(2)成立.证明略
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
七年级数学下册第八章整章水平测试(A)
一、试试你的身手(每小题3分,共24分)
1.由同一张底片冲洗出来的两张五寸照片的图案 全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片 全等图形(填“是”或“不是”).
2.中,和的平分线相交于点,若,则的度数为 .
3.“两个锐角对应相等” (填“能”或“不能”)判别两个直角三角形相等.
4.如图1,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B=20°,则∠C= .
5.在平面中,到一个三角形三边的距离相等的点共有 个,到一个三角形三边所在直线的距离相等的点有 个.
6.在△ABC中,∠C=90°,AD为△ABC角平分线,BC=40,AB=50,若BD∶DC=5∶ 3,则△ADB的面积为 .
7.如图2,∠ACB=∠DBC,要想说明△ABC≌△DCB,只需增加的一个条件是 .(只需填一个你认为合适的条件)
8.如图3,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=36cm2,AB=18cm,BC=12cm,则DE= cm.
二、相信你的选择(每小题3分,共24分)
1.下列说法:
(1)只有两个三角形才能完全重合;
(2)如果两个图形全等,它们的形状和大小一定都相同;
(3)两个正方形一定是全等形;
(4)边数相同的图形一定能互相重合.
其中错误说法的为( )
A.(1)(3) B.(1)(2)(3) C.(1)(3)(4) D.(1)(4)
2.如图4所示,△ABC≌△EDF,F、C在AE上,DF=BC,AB=ED,AE=20,FC=10, 则AC的长为( )
A.10 B.5 C.15 D.20
3.△ABC中,∠A=∠B,若与△ABC全等的三角形中有一个角为120°,则△ABC中等于120°的角为( )
A.∠A B.∠B C.∠C D.∠A或∠C
4.如图5,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE;(2)BC=EF;(3)AC=DF ;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F,以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )
A.(1)(5)(2) B.(1)(2)(3) C.(4)(6)(1) D.(2)(3)(4)
5.如图6,AC和BD交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )
A.AB=DC B.OB=OC C.∠A=∠D D.∠AOB=∠DOC
6.如图7,已知四边形ABCD中,AB∥CD,BC∥AD,点E,F在BD上,且BE=DF,图中全等三角形的对数是( )
A.3 B.4 C.5 D.6
7.如图8,△ABC是直角三角形,∠A=90°,BD是角平分线,AD=n,BC=m,则△BDC的面积是( )
A.mn B. C. D.
8.如图9,直线l1,l2,l3表示三条相互交叉的公路,现要建造一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B.两处 C.三处 D.四处
三、挑战你的技能(共60分)
1.(10分)沿着图中虚线,分别把图10的图形划分为两个全等图形.
2.(10分)如图11,AB∥CD,AB=CD,点B、E、F、D在一条直线上,∠A=∠C.
求证:AE=CF.
3.(10分)课本上说:“两个三角形的两条边和其中一边的对角对应相等时,这两个三角形不一定全等.”
(1)试找出在什么情况下,两边和其中一边的对角对应相等的两个三角形全等,画出图形.(写一种情况即可)
(2)请说出(1)中的道理.
4.(10分)如图12,△ABC中,∠ABC=45°,AD⊥BC于D,点E在AD上,且DE=CD.
求证:BE=AC.
5.(10分)已知,如图13,PB、PC分别是△ABC的外角平分线,且相交于点P.
求证:点P在∠A的平分线上.
6.(10分)如图14,四边形ABCD中,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD的延长线于F,图中有无和△ABE全等的三角形,请说明理由.
四、拓广探索(本题12分)
如图15(1),E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.
(1)求证:MB=MD,ME=MF;
(2)当E、F两点移动至如图15(2)所示的位置时,其余条件不变,上述结论是否成立?若成立,请加以证明.
参考答案:
一、1.是,不是 2. 3.不能 4. 5.1,4
6.375 7.或或(答案不惟一) 8.2.4
二、1~4.CCCD 5~8.BABD
三、1.略
2.证明略
3.(1)答案不惟一,现举一例,在两三角形都是直角三角形时成立,图略
(2)根据判定两个直角三角形全等的条件当,时,
由“HL”得
4.证明略
5.证明略
6.有,为,理由略
四、(1)证明略
(2)成立.证明略
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
