七年级数学下册第八章整章水平测试(B)
文档属性
| 名称 | 七年级数学下册第八章整章水平测试(B) |  | |
| 格式 | rar | ||
| 文件大小 | 92.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 五四学制版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-10 11:39:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
七年级数学下册第八章整章水平测试(B)
一、试试你的身手(每小题3分,共24分)
1.如图1,在△ABC中,AD=DE,AB=BE,∠A=80°,则∠CED= .
2.已知△ABC≌△DEF,A与D,B与E分别是对应顶点,∠A=52°,∠B=67°,BC=15cm,则∠F= ,FE= cm.
3.在△ABC中,∠C=90°,BC=4cm,∠BAC的平分线交BC于D,且BD∶DC=5∶3,则D到AB的距离为 .
4.如图2,△ABC是三边均不相等的三角形,DE=BC,以D、E为两个顶点画位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出 个.
5.如图3,AD、分别是锐角三角形ABC和锐角三角形中BC、边上的高,且、.若使△ABC≌△,请你补充条件 .(填写一个你认为适当的条件即可)
6.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是 .
7.如图4,已知在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于E,若BC=15cm,则△DEB的周长为 .
8.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CDE=35°,如图5,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是 .
二、相信你的选择(每小题3分,共24分)
1.下列各条件中,不能作出惟一三角形的是( )
A.已知两边和夹角 B.已知两角和夹边
C.已知两边和其中一边的对角 D.已知三边
2.下列各组条件中,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠C=∠F,AC=EF
C.AB=DE,BC=EF,△ABC的周长= △DEF的周长
D.∠A=∠D,∠B=∠E,∠C=∠F
3.如图6,在△ABC中,∠A∶∠B∶∠C=3∶5∶10,又△MNC≌△ABC,则∠BCM∶∠BCN等于( )
A.1∶2 B.1∶3 C.2∶3 D.1∶4
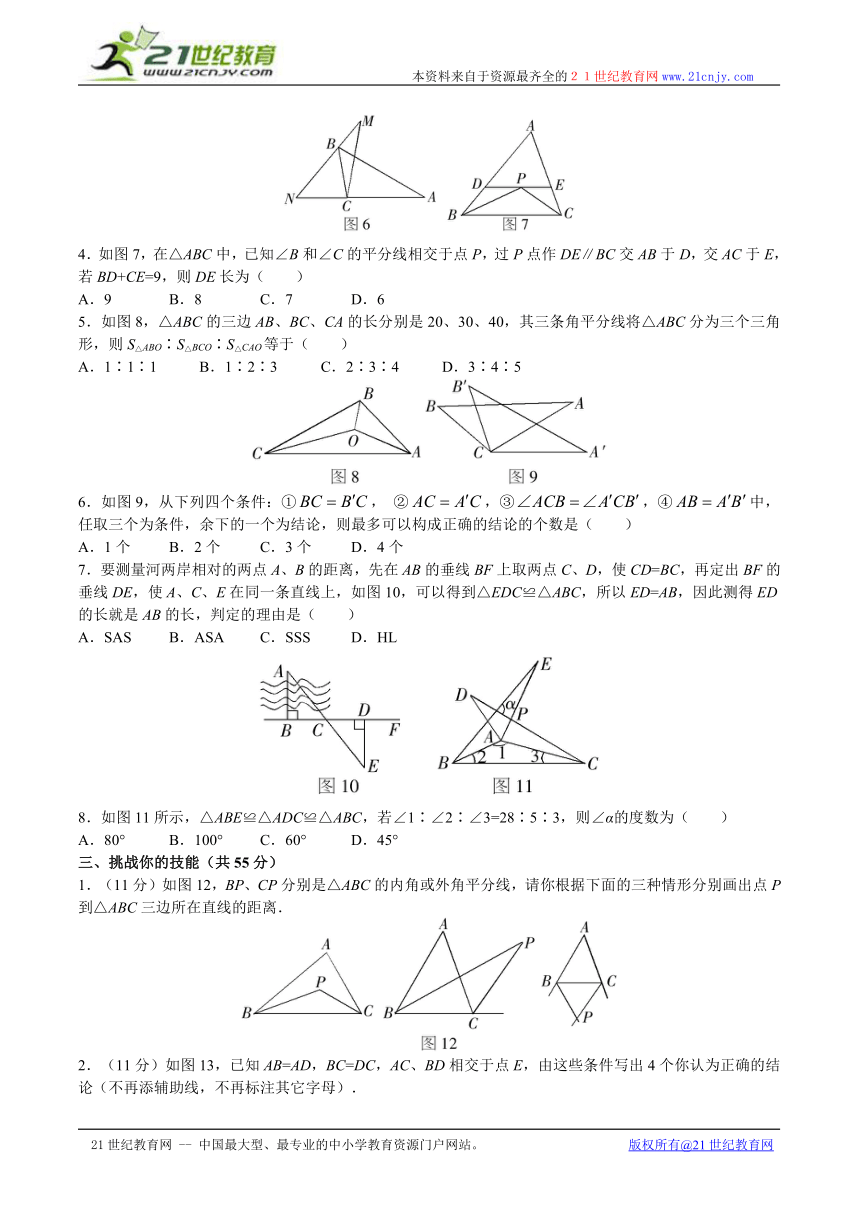
4.如图7,在△ABC中,已知∠B和∠C的平分线相交于点P,过P点作DE∥BC交AB于D,交AC于E,若BD+CE=9,则DE长为( )
A.9 B.8 C.7 D.6
5.如图8,△ABC的三边AB、BC、CA的长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于( )
A.1∶1∶1 B.1∶2∶3 C.2∶3∶4 D.3∶4∶5
6.如图9,从下列四个条件:①, ②,③,④中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
7.要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在同一条直线上,如图10,可以得到△EDC≌△ABC,所以ED=AB,因此测得ED的长就是AB的长,判定的理由是( )
A.SAS B.ASA C.SSS D.HL
8.如图11所示,△ABE≌△ADC≌△ABC,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为( )
A.80° B.100° C.60° D.45°
三、挑战你的技能(共55分)
1.(11分)如图12,BP、CP分别是△ABC的内角或外角平分线,请你根据下面的三种情形分别画出点P到△ABC三边所在直线的距离.
2.(11分)如图13,已知AB=AD,BC=DC,AC、BD相交于点E,由这些条件写出4个你认为正确的结论(不再添辅助线,不再标注其它字母).
3.(11分)如图14,公园有一条“Z”字形道路ABCD,其中AB∥CD,在E,M,F处各有一个小石凳,E、F分别在AB、CD上,且BE=CF,M为BC的中点,请问三个小石凳是否在一条直线上?说出你推断的理由.
4.(11分)如图15,给出五个等量关系:①AD=BC、②AC=BD、③CE=DE、④∠D=∠C、⑤∠DAB=∠CBA.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.
5.(11分)如图16,在∠AOB的两边OA、OB上分别取OM=ON,OD=OE,DN和EM相交于点C.
求证:点C在∠AOB的平分线上.
四、拓广探索(本题17分)
如图17,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连结EG,
(1)试判断△ABC与△AEG面积之间的关系,并说明理由.
(2)园林小路,曲径通幽,如图18所示,小路由白色的正方形大理石和黑色的三角形大理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,那么这条小路一共占地多少平方米?
参考答案:
一、1. 2.,15 3.1.5cm 4.4
5.(答案不惟一) 6.相等或互补 7.15cm 8.
二、1~4.CCDA 5~8.CBBA
三、1.提示:直接过点向各边所在直线做垂线即可
2.答案不惟一,如,,,,,等等
3.解:三个小石凳在一条直线上.理由略.
4.略,答案不惟一
5.证明略
四、(1)与面积相等,理由略
(2)这条小路的面积为平方米.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
七年级数学下册第八章整章水平测试(B)
一、试试你的身手(每小题3分,共24分)
1.如图1,在△ABC中,AD=DE,AB=BE,∠A=80°,则∠CED= .
2.已知△ABC≌△DEF,A与D,B与E分别是对应顶点,∠A=52°,∠B=67°,BC=15cm,则∠F= ,FE= cm.
3.在△ABC中,∠C=90°,BC=4cm,∠BAC的平分线交BC于D,且BD∶DC=5∶3,则D到AB的距离为 .
4.如图2,△ABC是三边均不相等的三角形,DE=BC,以D、E为两个顶点画位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出 个.
5.如图3,AD、分别是锐角三角形ABC和锐角三角形中BC、边上的高,且、.若使△ABC≌△,请你补充条件 .(填写一个你认为适当的条件即可)
6.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是 .
7.如图4,已知在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于E,若BC=15cm,则△DEB的周长为 .
8.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CDE=35°,如图5,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是 .
二、相信你的选择(每小题3分,共24分)
1.下列各条件中,不能作出惟一三角形的是( )
A.已知两边和夹角 B.已知两角和夹边
C.已知两边和其中一边的对角 D.已知三边
2.下列各组条件中,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠C=∠F,AC=EF
C.AB=DE,BC=EF,△ABC的周长= △DEF的周长
D.∠A=∠D,∠B=∠E,∠C=∠F
3.如图6,在△ABC中,∠A∶∠B∶∠C=3∶5∶10,又△MNC≌△ABC,则∠BCM∶∠BCN等于( )
A.1∶2 B.1∶3 C.2∶3 D.1∶4
4.如图7,在△ABC中,已知∠B和∠C的平分线相交于点P,过P点作DE∥BC交AB于D,交AC于E,若BD+CE=9,则DE长为( )
A.9 B.8 C.7 D.6
5.如图8,△ABC的三边AB、BC、CA的长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于( )
A.1∶1∶1 B.1∶2∶3 C.2∶3∶4 D.3∶4∶5
6.如图9,从下列四个条件:①, ②,③,④中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
7.要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在同一条直线上,如图10,可以得到△EDC≌△ABC,所以ED=AB,因此测得ED的长就是AB的长,判定的理由是( )
A.SAS B.ASA C.SSS D.HL
8.如图11所示,△ABE≌△ADC≌△ABC,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为( )
A.80° B.100° C.60° D.45°
三、挑战你的技能(共55分)
1.(11分)如图12,BP、CP分别是△ABC的内角或外角平分线,请你根据下面的三种情形分别画出点P到△ABC三边所在直线的距离.
2.(11分)如图13,已知AB=AD,BC=DC,AC、BD相交于点E,由这些条件写出4个你认为正确的结论(不再添辅助线,不再标注其它字母).
3.(11分)如图14,公园有一条“Z”字形道路ABCD,其中AB∥CD,在E,M,F处各有一个小石凳,E、F分别在AB、CD上,且BE=CF,M为BC的中点,请问三个小石凳是否在一条直线上?说出你推断的理由.
4.(11分)如图15,给出五个等量关系:①AD=BC、②AC=BD、③CE=DE、④∠D=∠C、⑤∠DAB=∠CBA.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.
5.(11分)如图16,在∠AOB的两边OA、OB上分别取OM=ON,OD=OE,DN和EM相交于点C.
求证:点C在∠AOB的平分线上.
四、拓广探索(本题17分)
如图17,以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连结EG,
(1)试判断△ABC与△AEG面积之间的关系,并说明理由.
(2)园林小路,曲径通幽,如图18所示,小路由白色的正方形大理石和黑色的三角形大理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,那么这条小路一共占地多少平方米?
参考答案:
一、1. 2.,15 3.1.5cm 4.4
5.(答案不惟一) 6.相等或互补 7.15cm 8.
二、1~4.CCDA 5~8.CBBA
三、1.提示:直接过点向各边所在直线做垂线即可
2.答案不惟一,如,,,,,等等
3.解:三个小石凳在一条直线上.理由略.
4.略,答案不惟一
5.证明略
四、(1)与面积相等,理由略
(2)这条小路的面积为平方米.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
