人教版数学六年级下册《鸽巢问题》课件
文档属性
| 名称 | 人教版数学六年级下册《鸽巢问题》课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-21 08:15:16 | ||
图片预览




文档简介
(共16张PPT)
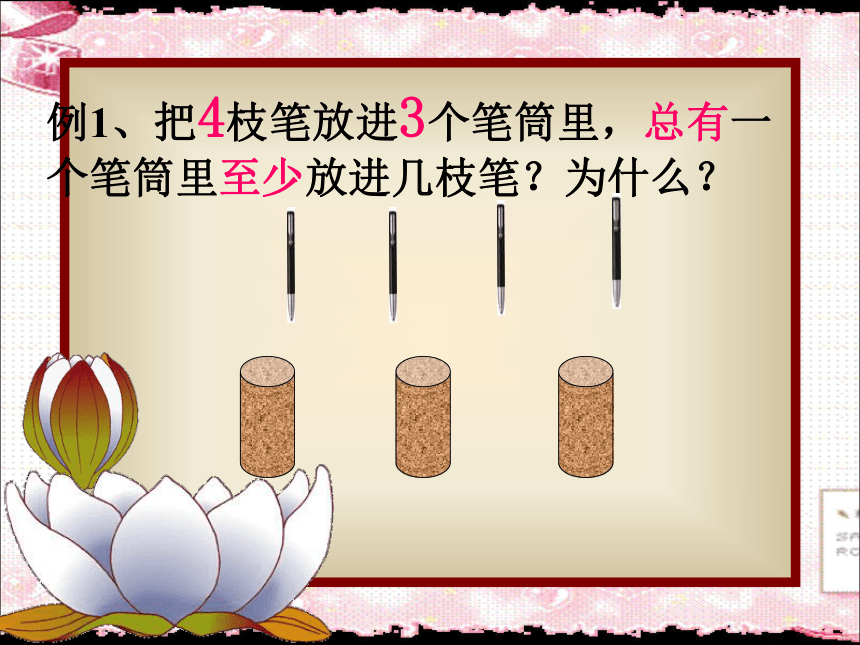
例1、把4枝笔放进3个笔筒里,总有一个笔筒里至少放进几枝笔?为什么?
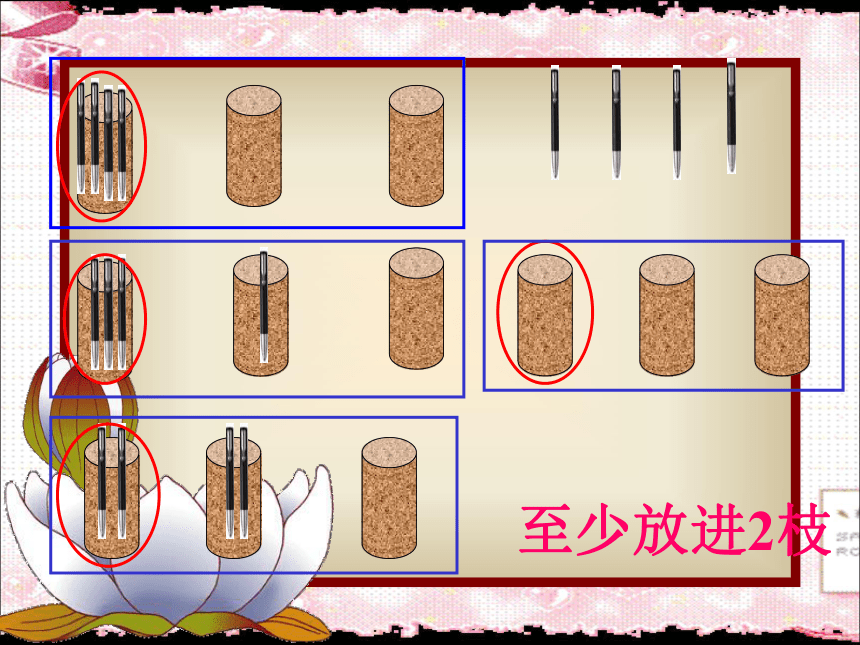
至少放进2枝
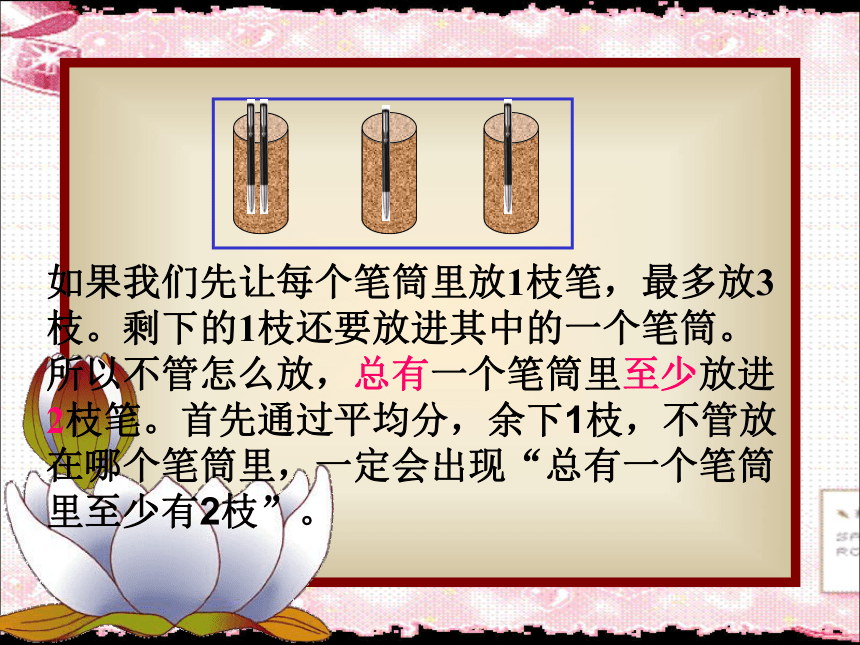
如果我们先让每个笔筒里放1枝笔,最多放3枝。剩下的1枝还要放进其中的一个笔筒。所以不管怎么放,总有一个笔筒里至少放进2枝笔。首先通过平均分,余下1枝,不管放在哪个笔筒里,一定会出现“总有一个笔筒里至少有2枝”。
把5枝笔放在4个笔筒里,还是不管怎么放,总有一个笔筒里至少放进了2枝笔吗?
为什么会有这样的结果?
这样分实际上是怎样分?怎样列式?
想一想:
放入物体的个数都比盒子(抽屉)数多1,不管怎么放,总有一个盒子里至少有2个物体。
“抽屉原理”又称“鸽巢原理”,
最先是由19世纪的德国数学家
狄利克雷提出来的,所以又称
“狄利克雷原理”。抽屉原理的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。
狄利克雷
(1805~1859)
例2 把7本书放进3个抽屉中.
不管怎么放,总有一个抽屉里至少放进3本书.
如果每个抽屉放2本书,最多放6本.剩下的1本放进其中的一个抽屉.所以至少有3本书放进同一个抽屉.
如果把10本书放进3个抽屉里呢
13本书放进3个抽屉呢
如果把8本书放进3个抽屉里,不管怎么放,总有一个抽屉里至少有几本书?
8÷3=2(本)……2(本)
1+1=2(本)
我们先让一个抽屉里放进2本书,3个抽屉最多可放进
6本书,还剩下2本,无论怎么放,都会至少有2本
书要放进同一个抽屉里。
至少数=商数+1
计算绝招
抽屉原理:
m÷n=a… …b ( m>n>1)
把m个物体放进n个抽屉里( m>n>1),不管怎么放总有一个抽屉至少放进( )个物体。
a+1
一幅扑克,拿走大、小王后还有52张牌,任意抽出其中的几张,总会有至少两张牌的花色相同,为什么?
这节课,我们主要学习了什么呢?
例1、把4枝笔放进3个笔筒里,总有一个笔筒里至少放进几枝笔?为什么?
至少放进2枝
如果我们先让每个笔筒里放1枝笔,最多放3枝。剩下的1枝还要放进其中的一个笔筒。所以不管怎么放,总有一个笔筒里至少放进2枝笔。首先通过平均分,余下1枝,不管放在哪个笔筒里,一定会出现“总有一个笔筒里至少有2枝”。
把5枝笔放在4个笔筒里,还是不管怎么放,总有一个笔筒里至少放进了2枝笔吗?
为什么会有这样的结果?
这样分实际上是怎样分?怎样列式?
想一想:
放入物体的个数都比盒子(抽屉)数多1,不管怎么放,总有一个盒子里至少有2个物体。
“抽屉原理”又称“鸽巢原理”,
最先是由19世纪的德国数学家
狄利克雷提出来的,所以又称
“狄利克雷原理”。抽屉原理的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。
狄利克雷
(1805~1859)
例2 把7本书放进3个抽屉中.
不管怎么放,总有一个抽屉里至少放进3本书.
如果每个抽屉放2本书,最多放6本.剩下的1本放进其中的一个抽屉.所以至少有3本书放进同一个抽屉.
如果把10本书放进3个抽屉里呢
13本书放进3个抽屉呢
如果把8本书放进3个抽屉里,不管怎么放,总有一个抽屉里至少有几本书?
8÷3=2(本)……2(本)
1+1=2(本)
我们先让一个抽屉里放进2本书,3个抽屉最多可放进
6本书,还剩下2本,无论怎么放,都会至少有2本
书要放进同一个抽屉里。
至少数=商数+1
计算绝招
抽屉原理:
m÷n=a… …b ( m>n>1)
把m个物体放进n个抽屉里( m>n>1),不管怎么放总有一个抽屉至少放进( )个物体。
a+1
一幅扑克,拿走大、小王后还有52张牌,任意抽出其中的几张,总会有至少两张牌的花色相同,为什么?
这节课,我们主要学习了什么呢?
