人教版数学九年级上册 21.3 实际问题与一元二次方程 学案 (含答案)
文档属性
| 名称 | 人教版数学九年级上册 21.3 实际问题与一元二次方程 学案 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 82.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 08:39:54 | ||
图片预览



文档简介
实际问题与一元二次方程小结
班级:_____________姓名:__________________组号:_________
一、巩固训练
1.解下列方程:
(1); (2); (3)。
2.列方程解应用题:
(1)一个矩形的长和宽相差,面积是。求这个矩形的长和宽。
(2)要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛,应邀请多少个球队参加比赛。
(3)利用一面墙(墙的长度不限),用长的篱笆,怎样围成一个面积为的矩形场地?
二、错题再现
1.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支。主干、支干和小分支的总数是91.每个支干长出多少小分支?
2.上海甲商场七月份利润为100万元,九月份的利率为121万元,乙商场七月份利率为200万元,九月份的利润为288万元,那么哪个商场利润的年平均上升率较大?
三、能力提升
1.小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件,如果一次性购买不超过10件,单价为80元;如果一次性购买多于10件,那么每增加1件,购买的所有服装的单价降低2元,但单价不得低于50元,按此优惠条件,小丽一次性购买这种服装付了1200元,请问她购买了多少件这种服装?
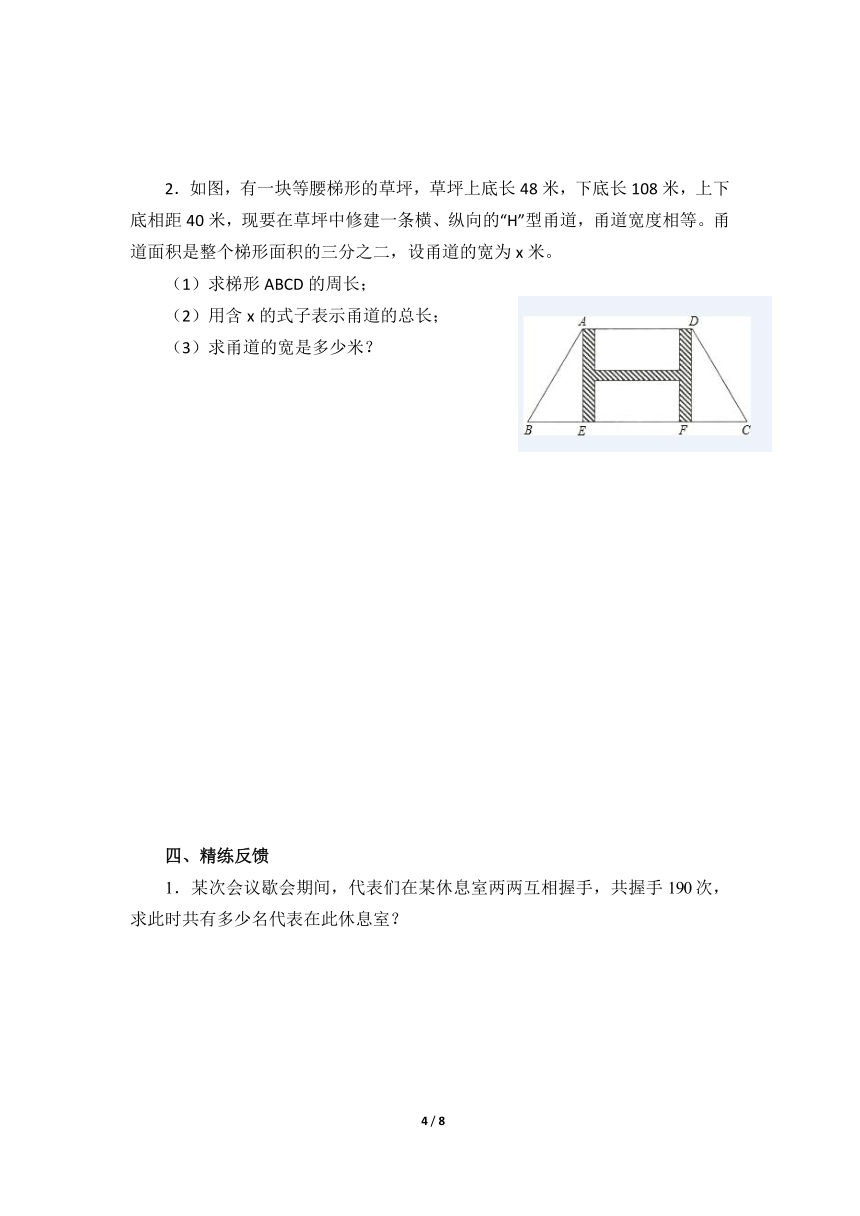
2.如图,有一块等腰梯形的草坪,草坪上底长48米,下底长108米,上下底相距40米,现要在草坪中修建一条横、纵向的“H”型甬道,甬道宽度相等。甬道面积是整个梯形面积的三分之二,设甬道的宽为x米。
(1)求梯形ABCD的周长;
(2)用含x的式子表示甬道的总长;
(3)求甬道的宽是多少米?
四、精练反馈
1.某次会议歇会期间,代表们在某休息室两两互相握手,共握手190次,求此时共有多少名代表在此休息室?
2.要在一块长16cm,宽12cm的矩形地上建造一个花园,要求花园占地面积为荒地的面积的一半,图(1)图(2)分别是小明和小红的设计方案。
小明:我设计的方案如图(1),花园四周小路宽度一致。
小红:我设计的方案如图(2),花园每个角上的扇形相同。
你能分别求出小明设计图中的道路宽及小红设计的扇形半径长吗?(π取3,)
【答案】
【巩固训练】
1.
;;
2.(1)解:设宽为xcm,则长为(x+3)cm
x(x+3)=4
x +3x-4=0
(x+4)(x-1)=0
x=-4(舍去)或x=1
x+3=1+3=4
答:这个矩形的宽为1cm、长为4cm。
(2)解:设邀请x个球队参加比赛,
依题意得∴x2-x-30=0,
∴x=6或x=-5(不合题意,舍去)。
答:应邀请6个球队参加比赛。
(3)解:设利用墙的长度为X米,则长方形场地的相邻边长为(20-X)/2米
X(20-X)=50
X(20-X)=100
X -20X+100=0
(X-10) =0
X=10
(20-10)/2=10/2=5米
答:这个长方形场地长为10米,宽为5米。长为10米宽为5米就可围成一个面积为50平方米的长方形场地
【错题再现】
1.解:设每个支干长出x个小分支
则1+x+x =91
x +x-90=(x+10)(x-9)=0
显然x>0
所以x=9
答:每个支干长出9个分支
2.解:设甲商场的月平均上升率为x,乙商场的月平均上升率为y,
则依题意得:100(1+x)2=121
解得:x1=0.1,x2=-2.1(不合题意舍去)
∴x=0.1=10%
设乙商场的月平均上升率为y
则依题意得:
200(1+y)2=288
解得:y1=0.2,y2=-2.2(不合题意舍去)
∴y=0.2=20%
∵0.1<0.2,
∴乙商场的月平均上升率较大
答:乙商场的月平均上升率较大。
【能力提升】
1.解:设购买了x件这种服装且多于10件,根据题意得出:
[80-2(x-10)]x=1200,
解得:x1=20,x2=30,
当x=20时,80-2(20-10)=60元>50元,符合题意;
当x=30时,80-2(30-10)=40元<50元,不合题意,舍去;
答:她购买了20件这种服装。
2.解:(1)在等腰梯形ABCD中,AD=EF=48,AE⊥BC,DF⊥BC
∴
∴梯形ABCD的周长=AB+BC+CD+DA=50+108+50+48=256(米)。
(2)甬道的总长:40×2+48-2x=(128-2x)米;
(3)根据题意,得
整理得:解之得
因60>48,不符合题意,舍去
答:甬道的宽为4米。
【精练反馈】
1.解:设小组有x人,由题意得:
x(x-1)=380;
解得:x=20或x=-19(舍去)
答:共有20名代表休息。
2.(1)设小路宽xm,则得方程(16-2x)(12-2x)=×16×12,
解得:x1=2;x2=12,
而矩形的宽为12m,若小路宽为12m,不符合实际情况,故x2=12m不合题意;
故小明设计图中的道路的宽为2米。
(2)由题意得:=×16×12,
解得:x1=-4(不合题意舍去),x2=4≈5.5,
答:小红的设计方案中扇形的半径约为5.5m。
1 / 8
班级:_____________姓名:__________________组号:_________
一、巩固训练
1.解下列方程:
(1); (2); (3)。
2.列方程解应用题:
(1)一个矩形的长和宽相差,面积是。求这个矩形的长和宽。
(2)要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛,应邀请多少个球队参加比赛。
(3)利用一面墙(墙的长度不限),用长的篱笆,怎样围成一个面积为的矩形场地?
二、错题再现
1.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支。主干、支干和小分支的总数是91.每个支干长出多少小分支?
2.上海甲商场七月份利润为100万元,九月份的利率为121万元,乙商场七月份利率为200万元,九月份的利润为288万元,那么哪个商场利润的年平均上升率较大?
三、能力提升
1.小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件,如果一次性购买不超过10件,单价为80元;如果一次性购买多于10件,那么每增加1件,购买的所有服装的单价降低2元,但单价不得低于50元,按此优惠条件,小丽一次性购买这种服装付了1200元,请问她购买了多少件这种服装?
2.如图,有一块等腰梯形的草坪,草坪上底长48米,下底长108米,上下底相距40米,现要在草坪中修建一条横、纵向的“H”型甬道,甬道宽度相等。甬道面积是整个梯形面积的三分之二,设甬道的宽为x米。
(1)求梯形ABCD的周长;
(2)用含x的式子表示甬道的总长;
(3)求甬道的宽是多少米?
四、精练反馈
1.某次会议歇会期间,代表们在某休息室两两互相握手,共握手190次,求此时共有多少名代表在此休息室?
2.要在一块长16cm,宽12cm的矩形地上建造一个花园,要求花园占地面积为荒地的面积的一半,图(1)图(2)分别是小明和小红的设计方案。
小明:我设计的方案如图(1),花园四周小路宽度一致。
小红:我设计的方案如图(2),花园每个角上的扇形相同。
你能分别求出小明设计图中的道路宽及小红设计的扇形半径长吗?(π取3,)
【答案】
【巩固训练】
1.
;;
2.(1)解:设宽为xcm,则长为(x+3)cm
x(x+3)=4
x +3x-4=0
(x+4)(x-1)=0
x=-4(舍去)或x=1
x+3=1+3=4
答:这个矩形的宽为1cm、长为4cm。
(2)解:设邀请x个球队参加比赛,
依题意得∴x2-x-30=0,
∴x=6或x=-5(不合题意,舍去)。
答:应邀请6个球队参加比赛。
(3)解:设利用墙的长度为X米,则长方形场地的相邻边长为(20-X)/2米
X(20-X)=50
X(20-X)=100
X -20X+100=0
(X-10) =0
X=10
(20-10)/2=10/2=5米
答:这个长方形场地长为10米,宽为5米。长为10米宽为5米就可围成一个面积为50平方米的长方形场地
【错题再现】
1.解:设每个支干长出x个小分支
则1+x+x =91
x +x-90=(x+10)(x-9)=0
显然x>0
所以x=9
答:每个支干长出9个分支
2.解:设甲商场的月平均上升率为x,乙商场的月平均上升率为y,
则依题意得:100(1+x)2=121
解得:x1=0.1,x2=-2.1(不合题意舍去)
∴x=0.1=10%
设乙商场的月平均上升率为y
则依题意得:
200(1+y)2=288
解得:y1=0.2,y2=-2.2(不合题意舍去)
∴y=0.2=20%
∵0.1<0.2,
∴乙商场的月平均上升率较大
答:乙商场的月平均上升率较大。
【能力提升】
1.解:设购买了x件这种服装且多于10件,根据题意得出:
[80-2(x-10)]x=1200,
解得:x1=20,x2=30,
当x=20时,80-2(20-10)=60元>50元,符合题意;
当x=30时,80-2(30-10)=40元<50元,不合题意,舍去;
答:她购买了20件这种服装。
2.解:(1)在等腰梯形ABCD中,AD=EF=48,AE⊥BC,DF⊥BC
∴
∴梯形ABCD的周长=AB+BC+CD+DA=50+108+50+48=256(米)。
(2)甬道的总长:40×2+48-2x=(128-2x)米;
(3)根据题意,得
整理得:解之得
因60>48,不符合题意,舍去
答:甬道的宽为4米。
【精练反馈】
1.解:设小组有x人,由题意得:
x(x-1)=380;
解得:x=20或x=-19(舍去)
答:共有20名代表休息。
2.(1)设小路宽xm,则得方程(16-2x)(12-2x)=×16×12,
解得:x1=2;x2=12,
而矩形的宽为12m,若小路宽为12m,不符合实际情况,故x2=12m不合题意;
故小明设计图中的道路的宽为2米。
(2)由题意得:=×16×12,
解得:x1=-4(不合题意舍去),x2=4≈5.5,
答:小红的设计方案中扇形的半径约为5.5m。
1 / 8
同课章节目录
