第23章 解直角三角形 单元达标测试卷(含答案) 2023-2024学年沪科版九年级数学上册
文档属性
| 名称 | 第23章 解直角三角形 单元达标测试卷(含答案) 2023-2024学年沪科版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 401.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 10:43:18 | ||
图片预览



文档简介
沪科版九年级数学上册第23章解直角三角形单元达标测试卷
一、单选题
1.如图,在平面直角坐标系中,点A坐标为(8,6),那么cos 的值是( )
A. B. C. D.
2.已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A. B. C. D.2
3.已知,△ABC中,∠C=90°,sinA=,则∠A 的度数是 ( )
A.30° B.45° C.60° D.90°
4.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
5.如图所示,在 中, , ,点D在 边上, ,则 的长为( )
A. B. C. D.
6.α为锐角,若sinα+cosα= ,则sinα﹣cosα的值为( )
A. B.± C. D.0
7.在正方形网格中,△ABC的位置如图所示,则cosB的值为( )
A. B. C. D.
8.在直角坐标平面内有一点P(3,4),OP与x轴正半轴的夹角为 ,则 的值( )
A. B. C. D.
9.已知在Rt△ABC中,∠C=90°,sinA= ,AC=2 ,那么BC的值为( )
A.2 B.4 C.4 D.6
10.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sin∠B的值为( )
A. B. C. D.
二、填空题
11.若∠A为锐角,且tanA=1,则∠A的度数为 .
12.如图,沿倾斜角为30°的山坡植树,要求相邻两棵树间的水平距离AC为2m,那么相邻两棵树的斜坡距离AB约为 m.(结果精确到0.1m)
13.在数学活动课上名师带领学生去测量河两岸A,B两处之间的距离,先从A处出发与AB成90°方向,向前走了10米到C处,在C处测得∠ACB=60°(如图所示),那么A,B之间的距离约为 米(计算结果精确到0.1米)
14.如图,在中,,,,点O是的中点,点D是线段上任意一点(不含端点),连接,则的最小值为 .
三、解答题
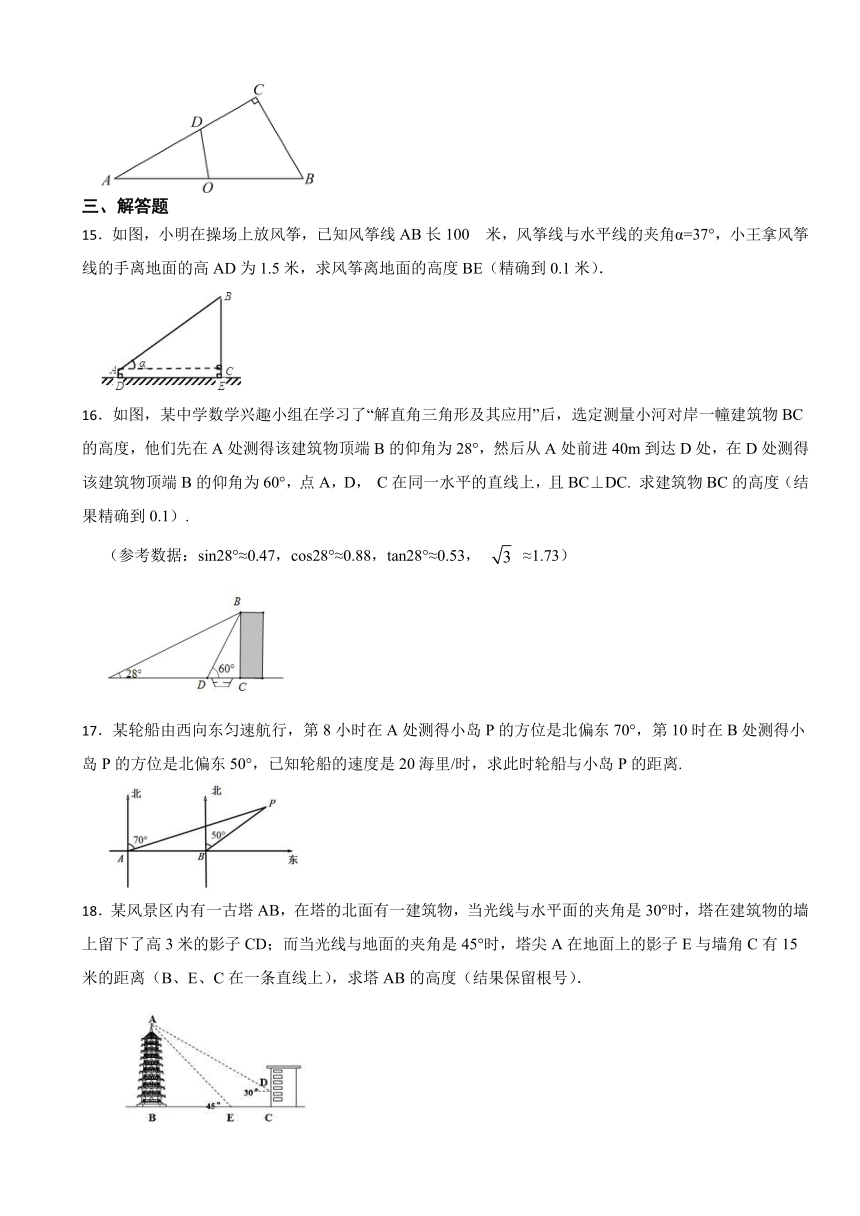
15.如图,小明在操场上放风筝,已知风筝线AB长100 米,风筝线与水平线的夹角α=37°,小王拿风筝线的手离地面的高AD为1.5米,求风筝离地面的高度BE(精确到0.1米).
16.如图,某中学数学兴趣小组在学习了“解直角三角形及其应用”后,选定测量小河对岸一幢建筑物BC的高度,他们先在A处测得该建筑物顶端B的仰角为28°,然后从A处前进40m到达D处,在D处测得该建筑物顶端B的仰角为60°,点A,D, C在同一水平的直线上,且BC⊥DC. 求建筑物BC的高度(结果精确到0.1).
(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53, ≈1.73)
17.某轮船由西向东匀速航行,第8小时在A处测得小岛P的方位是北偏东70°,第10时在B处测得小岛P的方位是北偏东50°,已知轮船的速度是20海里/时,求此时轮船与小岛P的距离.
18.某风景区内有一古塔AB,在塔的北面有一建筑物,当光线与水平面的夹角是30°时,塔在建筑物的墙上留下了高3米的影子CD;而当光线与地面的夹角是45°时,塔尖A在地面上的影子E与墙角C有15米的距离(B、E、C在一条直线上),求塔AB的高度(结果保留根号).
四、综合题
19.在△ABC中,∠C=90°.
(1)已知c=8,∠A=60°,求∠B,a,b;
(2)已知a=3,∠A=45°,求∠B,b,c.
20.如图,在正方形ABCD中,点G在边BC上(不与点B,C重合),连接AG,作DE⊥AG,于点E,BF⊥AG于点F,设 。
(1)求证:AE=BF;
(2)连接BE,DF,设∠EDF= ,∠EBF= 求证:
(3)设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2,求 的最大值.
21.如图所示的方格纸是由9个大小完全一样的小正方形组成的.点A、B、C、D均在方格纸的格点(即图中小正方形的顶点)上,线段AB与线段CD相交于点E.设图中每个小正方形的边长均为1.
(1)求证:AB⊥CD;
(2)求sin∠BCD的值.
22.如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(﹣1,0)、B(3,0).
(1)求抛物线的解析式;
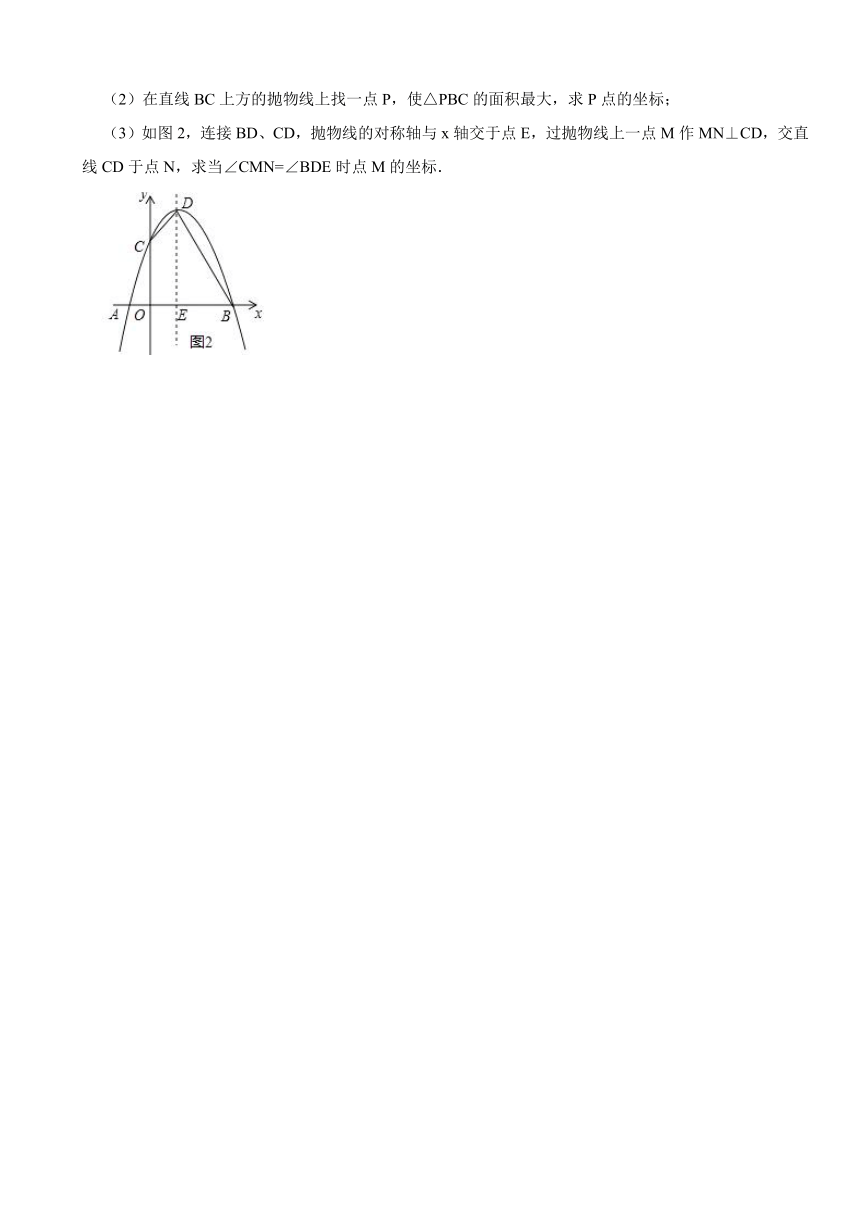
(2)在直线BC上方的抛物线上找一点P,使△PBC的面积最大,求P点的坐标;
(3)如图2,连接BD、CD,抛物线的对称轴与x轴交于点E,过抛物线上一点M作MN⊥CD,交直线CD于点N,求当∠CMN=∠BDE时点M的坐标.
答案解析部分
1.【答案】D
【解析】【解答】cos = ,故答案为:D.
故答案为:D.
【分析】由点A的坐标为(8,6),根据锐角三角函数的定义即可求解.
2.【答案】D
【解析】【解答】解:令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,不妨设A(﹣3,0),B(1,0),
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点C(﹣1,4),
如图所示,作CD⊥AB于D.
在Rt△ACD中,tan∠CAD= = =2,
故答案为D.
【分析】先求出A、B、C坐标,作CD⊥AB于D,根据tan∠ACD= 即可计算.本题考查二次函数与x轴交点坐标,锐角三角函数的定义,解题的关键是熟练掌握求抛物线与x轴交点坐标的方法,记住锐角三角函数的定义,属于中考常考题型.
3.【答案】C
【解析】【解答】因为sinA=
所以∠A=60°
故选C
4.【答案】A
【解析】【解答】因为△ABC三边的长度都扩大为原来的3倍所得的三角形与原三角形相似,所以锐角A的大小没改变,所以锐角A的正弦函数值也不变.
故答案为:A.
【分析】根据正弦函数的定义,利用分式的基本性质进行化简,从而可得函数值的变化情况.
5.【答案】C
【解析】【解答】解:∵
∴ ,即 ,
∴ ,
∴ ,
∴ ,
∴ .
故答案为:C.
【分析】利用解直角三角形求出BC的长,利用勾股定理求出AC的长,由此可得到CD的长;然后根据BD=BC-CD,可求出BD的长.
6.【答案】D
【解析】【解答】解:∵sinα+cosα= ,
∴(sinα+cosα)2=2,
即sin2α+cos2α+2sinαcosα=2.
又∵sin2α+cos2α=1,
∴2sinαcosα=1.
∴(sinα﹣cosα)2=sin2α+cos2α﹣2sinαcosα=1﹣2sinαcosα=1﹣1=0.
∴sinα﹣cosα=0.
故答案为:D.
【分析】根据等式的性质,将sinα+cosα= ,两边同时平方得出(sinα+cosα)2=2,即sin2α+cos2α+2sinαcosα=2.根据同一个锐角的正弦函数值与余弦函数值的关系得出sin2α+cos2α=1,故2sinαcosα=1.再根据完全平方公式即整体代入得出(sinα﹣cosα)2=sin2α+cos2α﹣2sinαcosα=1﹣2sinαcosα=1﹣1=0,最后根据0的2次幂等于0,即可得出答案。
7.【答案】B
【解析】【分析】根据格点的特征及勾股定理结合余弦的定义即可求得结果,△ABC为钝角三角形,角B的余弦需要构造直角三角形找邻边和斜边,如图过A作AD垂直于BC的延长线于D点,
.
【解答】由图可得,故选B.
【点评】解题的关键是熟练掌握余弦的定义:余弦=邻边:斜边,注意函数值的大小只与角的大小有关.
8.【答案】D
【解析】【解答】解:由点P(3,4)可得点P到x轴、y轴的距离为4、3,则 ,
∵OP与x轴正半轴的夹角为 ,
∴ ;
故答案为:D.
【分析】先求出OP的长,再利用三角函数中的正弦的定义求解即可。
9.【答案】A
【解析】【解答】解:∵sinA= ,∴∠A=30°.
∴tan30°= ,
∴BC=2.
故选A.
【分析】由sin A= 求出∠A度数;根据三角函数的定义建立边角之间的关系求解.
10.【答案】A
【解析】【解答】如图,
∵∠C=90°,AB=4,BC=3,
∴,
∴;
故答案为:A.
【分析】先利用勾股定理求出AC的长,再利用正弦的定义可得。
11.【答案】45°
【解析】【解答】∵∠A为锐角,且tanA=1,tan45°=1,
∴∠A=45°.
故答案为:45°.
【分析】根据特殊角的三角函数值进行解答即可.
12.【答案】2.3
【解析】【解答】解:由题意可得,cos30°= = .
∴AB= ≈2.3.
【分析】利用30°的余弦函数求解.
13.【答案】17.3
【解析】【解答】解:由题意得∠A=90°,AC=10m,∠ACB=60°
∴AB=AC tan∠ACB=10×tan60°=10× =10 ≈17.3(米)
故答案为17.3.
【分析】由题意得∠A=90°,AC=10m,∠ACB=60°,然后在Rt△ABC中,利用正切函数即可求出A,B之间的距离.
14.【答案】
【解析】【解答】解:如图,过点C作CM∥AB,过点D作DE⊥AB于点E,交CM于点F,
∵EF⊥AB,
∴∠AED=90°,
∵AB∥CM,∠A=30°,
∴∠CFD=90°,∠MCA=∠A=30°,
∴DF=CD,
∴OD+CD=OD+DF,
当O、D、F三点共线时,OD+DF=OF最小,
过点O作OF'⊥CM于点F',交CA于点D',此时OD'+F'D'=OF'即为最小值,
在Rt△ABC中,∠ACB=90°,点O是AB的中点,
∴OA=OC=AB=,
∴∠A=∠ACO=30°,
∴∠F'CO=60°,
∴cos∠F'CO=,
∴OF'=,即OD+CD的最小值为.
故答案为:.
【分析】过点C作CM∥AB,过点D作DE⊥AB于点E,交CM于点F,根据平行线的性质可得∠CFD=90°,∠MCA=∠A=30°,由含30°角直角三角形性质得DF=CD,则OD+CD=OD+DF,当O、D、F三点共线时,OD+DF=OF最小,过点O作OF'⊥CM于点F',交CA于点D',此时OD'+F'D'=OF'即为最小值,由直角三角形斜边上的中线等于斜边的一半得OA=OC=AB=,由等边对等角得∠A=∠ACO=30°,则∠F'CO=60°,由∠F'CO的余弦函数及特殊锐角三角函数值可求出OF'的长,从而得出答案.
15.【答案】解:∵AB=100米,α=37°,∴BC=AB sinα=100sin37°,∵AD=CE=1.5米,∴BE=BC+CE=100×sin37°+1.5≈100×0.60+1.5=61.5(米),答:风筝离地面的高度BE为:61.5米
【解析】【分析】根据正弦函数的定义,由BC=AB sinα得出BC的长,根据矩形的性质得出AD=CE,根据线段的和差即可得出答案。
16.【答案】解:在 中, ,
∴ ,
∴ ,
在 中, ,
∴ .
∴ .
∴
∴ ,
∴
答:建筑物BC的高度约为30.6m.
【解析】【分析】在Rt△BCD中,利用解直角三角形用含DC的代数式表示出BC的长;在Rt△ABC中,利用解直角三角形,可得到关于DC的方程,解方程求出CD的长;然后求出BC的长.
17.【答案】解:过P作PD⊥AB于点D.
∵∠PBD=90°-50°=40°
且∠PBD=∠PAB+∠APB,∠PAB=90-70=20°,
∴∠APB=20°,
∴∠PAB=∠APB
∴BP=AB=20×2=40(海里)
∴求此时轮船与小岛P的距离是40海里.
【解析】【分析】过P作AB的垂线PD,在直角△BPD中可以求的∠PAD的度数是30度,即可证明△APB是等腰三角形,即可求解.
18.【答案】解:如图,过点D作DF⊥AB,垂足为F,∵AB⊥BC,CD⊥BC,
∴四边形BCDF的矩形,∴BC=DF,CD=BF,
设AB=x米,在Rt△ABE中,∠AEB=∠BAE=45°,∴BE=AB=x,
在Rt△ADF中,∠ADF=30°,AF=AB-BF=x-3,∴DF=AF cot30°= (x-3),
∵DF=BC=BE+EC,∴ (x-3)=x+15,解得x=12+9 ,
答:塔AB的高度(12+9 )米.
【解析】【解答】解:如图,过点D作DF⊥AB,垂足为F,
∵AB⊥BC,CD⊥BC,
∴四边形BCDF的矩形,∴BC=DF,CD=BF,
设AB=x米,在Rt△ABE中,∠AEB=∠BAE=45°,∴BE=AB=x,
在Rt△ADF中,∠ADF=30°,AF=AB-BF=x-3,∴DF=AF cot30°= (x-3),
∵DF=BC=BE+EC,∴ (x-3)=x+15,解得x=12+9 ,
答:塔AB的高度(12+9 )米.
【分析】分析题目过点D作DF⊥AB易证四边形BCDF的矩形,可得矩形的对边相等,设AB=x,在等腰直角△ABE中可得BE=AB,进而在直角△ADF中,利用三角函数关系表示出DF的长,再结合BC=DF得到关于x的方程,求解即可。
19.【答案】(1)解:△ABC中,∠C=90°,∠A=60°,
,
c=8,
,
(2)解:
△ABC中,∠C=90°,∠A=45°,
,
a=3
,
【解析】【分析】(1)根据内角和定理可得∠B=30°,然后根据三角函数的概念进行计算;
(2)根据内角和定理可得∠B=45°,然后根据三角函数的概念进行计算.
20.【答案】(1)证明:因为四边形ABCD是正方形,所以∠BAF+∠EAD=90°,又因为DE⊥AG,所以∠EAD+∠ADE=90°,所以∠ADE=∠BAF,
又因为BF⊥AG,所以∠DEA=∠AFB=90°,
又因为AD=AB所以Rt△DAE≌Rt△ABF,所以AE=BF
(2)证明:易知Rt△BFG∽Rt△DEA,所以 在Rt△DEF和Rt△BEF中,
tanα= ,tanβ= 所以ktanβ= = = = =tanα
所以
(3)解:设正方形ABCD的边长为1,则BG=k,所以△ABG的面积等于 k因为△ABD的面积等于 又因为 =k,所以S1=
所以S2=1- k- = 所以 =-k2+k+1= ≤
因为0<k<1,所以当k= ,即点G为BC中点时, 有最大值
【解析】
【分析】(1)根据正方形的性质,可证得AD=AB,同时利用余角的性质,可证得∠ADE=∠BAF,∠DEA=∠AFB,然后根据AAS可证Rt△DAE≌Rt△ABF,利用全等三角形的对应边相等,可证得结论。
(2)利用已知条件易证Rt△BFG∽Rt△DEA,利用相似三角形的对应边成比例,可证得 ,再利用解直角三角形分别求出tanα,tanβ,从而可以推出ktanβ=tanα。
(3)设正方形ABCD的边长为1,则BG=k,用含k的代数式可以表示出△ABG的面积,再分别用含k的代数式表示出S1,S2,然后求出S1与S2的比关于k的函数解析式,将函数解析式转化为顶点式,利用二次函数的性质,可求出S1与S2的比的最大值。
21.【答案】(1)证明:如图,
, , ,
,
,
又 ,
,
,
;
(2)解:在 中, , ,
,
同理, ,
,
,
,
解得 ,
.
【解析】【分析】(1)证明 ,可得 ,根据同角的余角相等可得结论;(2)根据勾股定理先计算 和 的长,根据面积法可得 的长,最后由三角函数定义可得结论.
22.【答案】(1)解:将A(﹣1,0)、B(3,0)两点代入y=ax2+bx+3得: ,解得:a﹣1,b=2.
∴抛物线的表达式为:y=﹣x2+2x+3
(2)解:由题意设P(x,﹣x2+2x+3),过点P作x轴的垂线,交直线BC于点Q.
将x=0代入抛物线的解析式得:y=3,
∴点C的坐标为(0,3).
设直线BC的解析式为y=kx+b,将点B,C的坐标代入得: ,
解得:k=﹣1,b=3.
∴直线CB解析式:y=﹣x+3,则Q(x,﹣x+3)
∴PQ=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x.
∴S△BCD= PQ OB= ×(﹣x2+3x)×3=﹣ (x﹣ )2+ .
∴当x= 时,S△BCD取最大值,
此时P( , ).
(3)解:∵抛物线y=﹣(x﹣3)(x+1)=﹣x2+2x+3与与y轴交于点C,
∴C点坐标为(0,3),顶点(1,4),E(1,0)
∴tan∠BDE= = .
①当点M在对称轴的右侧时.
(i)作当点N在射线CD上时,如图2,过点N作y轴的垂线,垂足为G,
过点M作GN的垂线,垂足为H,则△CNG,△MNH均为等腰直角三角形.
∵∠CMN=∠BDE,
∴tan∠CMN=tan∠BDE= = .
∴△CNG,△MNH相似比为1:2
设CG=a,则NG=a,NH=NH=2a,
∴M(3a,3+a﹣2a),即M(3a,3﹣a),
将点M的坐标代入抛物线的解析式得:﹣(3a)2+2×3a+3=3﹣a,解得:a=0(舍去)或a=
此时M( , ).
(ii)若点N在射线DC上,如图3,过点N作x轴的垂线l,分别过点M、C作GN的垂线,垂足为H、G,则△CNG,△MNH均为等腰直角三角形,
∵∠CMN=∠BDE,
∴tan∠CMN=tan∠BDE= = ,
∴△CNG与△MNH相似比为1:2
设CG=a,则NG=a,NH=NH=2a,
∴M(a,3﹣a﹣2a),即M(a,3﹣3a),
将点M的坐标代入抛物线的解析式得:﹣a2+2a+3=3﹣3a,解得:a=0(舍去)或a=5,此时M(5,12)
②当点M在对称轴左侧时.
∵∠CMN=∠BDE<45°,
∴∠MCN>45°,
∵抛物线左侧任意一点K,都有∠KCN<45°,
∴点M不存在.
综上可知,点M坐标为( , )或(5,12)
【解析】【分析】(1)将A(﹣1,0)、B(3,0)两点代入得到关于a、b的方程组,可求得a、b的值;(2)由题意设P(x,﹣x2+2x+3),过点P作x轴的垂线,交直线BC于点Q.先求得直线BC的解析式,则得到Q(x,﹣x+3),然后列出△BCD的面积与x的关系式,利用配方法可求得点P的横坐标以及△CBD的面积的最大值;(3)首先求得C点坐标为(0,3),顶点(1,4),E(1,0)则tan∠BDE= .①当点M在对称轴的右侧时,作当点N在射线CD上时,如图1,过点N作y轴的垂线,垂足为G,过点M作GN的垂线,垂足为H,则△CNG,△MNH均为等腰直角三角形.设CG=a,用含a的式子表示点M的坐标,然后将点M的坐标代入抛物线的解析式可求得a的值;若点N在射线DC上,如图,过点N作x轴的垂线l,分别过点M、C作GN的垂线,垂足为H、G,则△CNG,△MNH均为等腰直角三角形,同理可求得此时a的值;②当点M在对称轴左侧时,抛物线左侧任意一点K,都有∠KCN<45°.
一、单选题
1.如图,在平面直角坐标系中,点A坐标为(8,6),那么cos 的值是( )
A. B. C. D.
2.已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A. B. C. D.2
3.已知,△ABC中,∠C=90°,sinA=,则∠A 的度数是 ( )
A.30° B.45° C.60° D.90°
4.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
5.如图所示,在 中, , ,点D在 边上, ,则 的长为( )
A. B. C. D.
6.α为锐角,若sinα+cosα= ,则sinα﹣cosα的值为( )
A. B.± C. D.0
7.在正方形网格中,△ABC的位置如图所示,则cosB的值为( )
A. B. C. D.
8.在直角坐标平面内有一点P(3,4),OP与x轴正半轴的夹角为 ,则 的值( )
A. B. C. D.
9.已知在Rt△ABC中,∠C=90°,sinA= ,AC=2 ,那么BC的值为( )
A.2 B.4 C.4 D.6
10.在Rt△ABC中,∠C=90°,AB=4,BC=3,则sin∠B的值为( )
A. B. C. D.
二、填空题
11.若∠A为锐角,且tanA=1,则∠A的度数为 .
12.如图,沿倾斜角为30°的山坡植树,要求相邻两棵树间的水平距离AC为2m,那么相邻两棵树的斜坡距离AB约为 m.(结果精确到0.1m)
13.在数学活动课上名师带领学生去测量河两岸A,B两处之间的距离,先从A处出发与AB成90°方向,向前走了10米到C处,在C处测得∠ACB=60°(如图所示),那么A,B之间的距离约为 米(计算结果精确到0.1米)
14.如图,在中,,,,点O是的中点,点D是线段上任意一点(不含端点),连接,则的最小值为 .
三、解答题
15.如图,小明在操场上放风筝,已知风筝线AB长100 米,风筝线与水平线的夹角α=37°,小王拿风筝线的手离地面的高AD为1.5米,求风筝离地面的高度BE(精确到0.1米).
16.如图,某中学数学兴趣小组在学习了“解直角三角形及其应用”后,选定测量小河对岸一幢建筑物BC的高度,他们先在A处测得该建筑物顶端B的仰角为28°,然后从A处前进40m到达D处,在D处测得该建筑物顶端B的仰角为60°,点A,D, C在同一水平的直线上,且BC⊥DC. 求建筑物BC的高度(结果精确到0.1).
(参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53, ≈1.73)
17.某轮船由西向东匀速航行,第8小时在A处测得小岛P的方位是北偏东70°,第10时在B处测得小岛P的方位是北偏东50°,已知轮船的速度是20海里/时,求此时轮船与小岛P的距离.
18.某风景区内有一古塔AB,在塔的北面有一建筑物,当光线与水平面的夹角是30°时,塔在建筑物的墙上留下了高3米的影子CD;而当光线与地面的夹角是45°时,塔尖A在地面上的影子E与墙角C有15米的距离(B、E、C在一条直线上),求塔AB的高度(结果保留根号).
四、综合题
19.在△ABC中,∠C=90°.
(1)已知c=8,∠A=60°,求∠B,a,b;
(2)已知a=3,∠A=45°,求∠B,b,c.
20.如图,在正方形ABCD中,点G在边BC上(不与点B,C重合),连接AG,作DE⊥AG,于点E,BF⊥AG于点F,设 。
(1)求证:AE=BF;
(2)连接BE,DF,设∠EDF= ,∠EBF= 求证:
(3)设线段AG与对角线BD交于点H,△AHD和四边形CDHG的面积分别为S1和S2,求 的最大值.
21.如图所示的方格纸是由9个大小完全一样的小正方形组成的.点A、B、C、D均在方格纸的格点(即图中小正方形的顶点)上,线段AB与线段CD相交于点E.设图中每个小正方形的边长均为1.
(1)求证:AB⊥CD;
(2)求sin∠BCD的值.
22.如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(﹣1,0)、B(3,0).
(1)求抛物线的解析式;
(2)在直线BC上方的抛物线上找一点P,使△PBC的面积最大,求P点的坐标;
(3)如图2,连接BD、CD,抛物线的对称轴与x轴交于点E,过抛物线上一点M作MN⊥CD,交直线CD于点N,求当∠CMN=∠BDE时点M的坐标.
答案解析部分
1.【答案】D
【解析】【解答】cos = ,故答案为:D.
故答案为:D.
【分析】由点A的坐标为(8,6),根据锐角三角函数的定义即可求解.
2.【答案】D
【解析】【解答】解:令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,不妨设A(﹣3,0),B(1,0),
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点C(﹣1,4),
如图所示,作CD⊥AB于D.
在Rt△ACD中,tan∠CAD= = =2,
故答案为D.
【分析】先求出A、B、C坐标,作CD⊥AB于D,根据tan∠ACD= 即可计算.本题考查二次函数与x轴交点坐标,锐角三角函数的定义,解题的关键是熟练掌握求抛物线与x轴交点坐标的方法,记住锐角三角函数的定义,属于中考常考题型.
3.【答案】C
【解析】【解答】因为sinA=
所以∠A=60°
故选C
4.【答案】A
【解析】【解答】因为△ABC三边的长度都扩大为原来的3倍所得的三角形与原三角形相似,所以锐角A的大小没改变,所以锐角A的正弦函数值也不变.
故答案为:A.
【分析】根据正弦函数的定义,利用分式的基本性质进行化简,从而可得函数值的变化情况.
5.【答案】C
【解析】【解答】解:∵
∴ ,即 ,
∴ ,
∴ ,
∴ ,
∴ .
故答案为:C.
【分析】利用解直角三角形求出BC的长,利用勾股定理求出AC的长,由此可得到CD的长;然后根据BD=BC-CD,可求出BD的长.
6.【答案】D
【解析】【解答】解:∵sinα+cosα= ,
∴(sinα+cosα)2=2,
即sin2α+cos2α+2sinαcosα=2.
又∵sin2α+cos2α=1,
∴2sinαcosα=1.
∴(sinα﹣cosα)2=sin2α+cos2α﹣2sinαcosα=1﹣2sinαcosα=1﹣1=0.
∴sinα﹣cosα=0.
故答案为:D.
【分析】根据等式的性质,将sinα+cosα= ,两边同时平方得出(sinα+cosα)2=2,即sin2α+cos2α+2sinαcosα=2.根据同一个锐角的正弦函数值与余弦函数值的关系得出sin2α+cos2α=1,故2sinαcosα=1.再根据完全平方公式即整体代入得出(sinα﹣cosα)2=sin2α+cos2α﹣2sinαcosα=1﹣2sinαcosα=1﹣1=0,最后根据0的2次幂等于0,即可得出答案。
7.【答案】B
【解析】【分析】根据格点的特征及勾股定理结合余弦的定义即可求得结果,△ABC为钝角三角形,角B的余弦需要构造直角三角形找邻边和斜边,如图过A作AD垂直于BC的延长线于D点,
.
【解答】由图可得,故选B.
【点评】解题的关键是熟练掌握余弦的定义:余弦=邻边:斜边,注意函数值的大小只与角的大小有关.
8.【答案】D
【解析】【解答】解:由点P(3,4)可得点P到x轴、y轴的距离为4、3,则 ,
∵OP与x轴正半轴的夹角为 ,
∴ ;
故答案为:D.
【分析】先求出OP的长,再利用三角函数中的正弦的定义求解即可。
9.【答案】A
【解析】【解答】解:∵sinA= ,∴∠A=30°.
∴tan30°= ,
∴BC=2.
故选A.
【分析】由sin A= 求出∠A度数;根据三角函数的定义建立边角之间的关系求解.
10.【答案】A
【解析】【解答】如图,
∵∠C=90°,AB=4,BC=3,
∴,
∴;
故答案为:A.
【分析】先利用勾股定理求出AC的长,再利用正弦的定义可得。
11.【答案】45°
【解析】【解答】∵∠A为锐角,且tanA=1,tan45°=1,
∴∠A=45°.
故答案为:45°.
【分析】根据特殊角的三角函数值进行解答即可.
12.【答案】2.3
【解析】【解答】解:由题意可得,cos30°= = .
∴AB= ≈2.3.
【分析】利用30°的余弦函数求解.
13.【答案】17.3
【解析】【解答】解:由题意得∠A=90°,AC=10m,∠ACB=60°
∴AB=AC tan∠ACB=10×tan60°=10× =10 ≈17.3(米)
故答案为17.3.
【分析】由题意得∠A=90°,AC=10m,∠ACB=60°,然后在Rt△ABC中,利用正切函数即可求出A,B之间的距离.
14.【答案】
【解析】【解答】解:如图,过点C作CM∥AB,过点D作DE⊥AB于点E,交CM于点F,
∵EF⊥AB,
∴∠AED=90°,
∵AB∥CM,∠A=30°,
∴∠CFD=90°,∠MCA=∠A=30°,
∴DF=CD,
∴OD+CD=OD+DF,
当O、D、F三点共线时,OD+DF=OF最小,
过点O作OF'⊥CM于点F',交CA于点D',此时OD'+F'D'=OF'即为最小值,
在Rt△ABC中,∠ACB=90°,点O是AB的中点,
∴OA=OC=AB=,
∴∠A=∠ACO=30°,
∴∠F'CO=60°,
∴cos∠F'CO=,
∴OF'=,即OD+CD的最小值为.
故答案为:.
【分析】过点C作CM∥AB,过点D作DE⊥AB于点E,交CM于点F,根据平行线的性质可得∠CFD=90°,∠MCA=∠A=30°,由含30°角直角三角形性质得DF=CD,则OD+CD=OD+DF,当O、D、F三点共线时,OD+DF=OF最小,过点O作OF'⊥CM于点F',交CA于点D',此时OD'+F'D'=OF'即为最小值,由直角三角形斜边上的中线等于斜边的一半得OA=OC=AB=,由等边对等角得∠A=∠ACO=30°,则∠F'CO=60°,由∠F'CO的余弦函数及特殊锐角三角函数值可求出OF'的长,从而得出答案.
15.【答案】解:∵AB=100米,α=37°,∴BC=AB sinα=100sin37°,∵AD=CE=1.5米,∴BE=BC+CE=100×sin37°+1.5≈100×0.60+1.5=61.5(米),答:风筝离地面的高度BE为:61.5米
【解析】【分析】根据正弦函数的定义,由BC=AB sinα得出BC的长,根据矩形的性质得出AD=CE,根据线段的和差即可得出答案。
16.【答案】解:在 中, ,
∴ ,
∴ ,
在 中, ,
∴ .
∴ .
∴
∴ ,
∴
答:建筑物BC的高度约为30.6m.
【解析】【分析】在Rt△BCD中,利用解直角三角形用含DC的代数式表示出BC的长;在Rt△ABC中,利用解直角三角形,可得到关于DC的方程,解方程求出CD的长;然后求出BC的长.
17.【答案】解:过P作PD⊥AB于点D.
∵∠PBD=90°-50°=40°
且∠PBD=∠PAB+∠APB,∠PAB=90-70=20°,
∴∠APB=20°,
∴∠PAB=∠APB
∴BP=AB=20×2=40(海里)
∴求此时轮船与小岛P的距离是40海里.
【解析】【分析】过P作AB的垂线PD,在直角△BPD中可以求的∠PAD的度数是30度,即可证明△APB是等腰三角形,即可求解.
18.【答案】解:如图,过点D作DF⊥AB,垂足为F,∵AB⊥BC,CD⊥BC,
∴四边形BCDF的矩形,∴BC=DF,CD=BF,
设AB=x米,在Rt△ABE中,∠AEB=∠BAE=45°,∴BE=AB=x,
在Rt△ADF中,∠ADF=30°,AF=AB-BF=x-3,∴DF=AF cot30°= (x-3),
∵DF=BC=BE+EC,∴ (x-3)=x+15,解得x=12+9 ,
答:塔AB的高度(12+9 )米.
【解析】【解答】解:如图,过点D作DF⊥AB,垂足为F,
∵AB⊥BC,CD⊥BC,
∴四边形BCDF的矩形,∴BC=DF,CD=BF,
设AB=x米,在Rt△ABE中,∠AEB=∠BAE=45°,∴BE=AB=x,
在Rt△ADF中,∠ADF=30°,AF=AB-BF=x-3,∴DF=AF cot30°= (x-3),
∵DF=BC=BE+EC,∴ (x-3)=x+15,解得x=12+9 ,
答:塔AB的高度(12+9 )米.
【分析】分析题目过点D作DF⊥AB易证四边形BCDF的矩形,可得矩形的对边相等,设AB=x,在等腰直角△ABE中可得BE=AB,进而在直角△ADF中,利用三角函数关系表示出DF的长,再结合BC=DF得到关于x的方程,求解即可。
19.【答案】(1)解:△ABC中,∠C=90°,∠A=60°,
,
c=8,
,
(2)解:
△ABC中,∠C=90°,∠A=45°,
,
a=3
,
【解析】【分析】(1)根据内角和定理可得∠B=30°,然后根据三角函数的概念进行计算;
(2)根据内角和定理可得∠B=45°,然后根据三角函数的概念进行计算.
20.【答案】(1)证明:因为四边形ABCD是正方形,所以∠BAF+∠EAD=90°,又因为DE⊥AG,所以∠EAD+∠ADE=90°,所以∠ADE=∠BAF,
又因为BF⊥AG,所以∠DEA=∠AFB=90°,
又因为AD=AB所以Rt△DAE≌Rt△ABF,所以AE=BF
(2)证明:易知Rt△BFG∽Rt△DEA,所以 在Rt△DEF和Rt△BEF中,
tanα= ,tanβ= 所以ktanβ= = = = =tanα
所以
(3)解:设正方形ABCD的边长为1,则BG=k,所以△ABG的面积等于 k因为△ABD的面积等于 又因为 =k,所以S1=
所以S2=1- k- = 所以 =-k2+k+1= ≤
因为0<k<1,所以当k= ,即点G为BC中点时, 有最大值
【解析】
【分析】(1)根据正方形的性质,可证得AD=AB,同时利用余角的性质,可证得∠ADE=∠BAF,∠DEA=∠AFB,然后根据AAS可证Rt△DAE≌Rt△ABF,利用全等三角形的对应边相等,可证得结论。
(2)利用已知条件易证Rt△BFG∽Rt△DEA,利用相似三角形的对应边成比例,可证得 ,再利用解直角三角形分别求出tanα,tanβ,从而可以推出ktanβ=tanα。
(3)设正方形ABCD的边长为1,则BG=k,用含k的代数式可以表示出△ABG的面积,再分别用含k的代数式表示出S1,S2,然后求出S1与S2的比关于k的函数解析式,将函数解析式转化为顶点式,利用二次函数的性质,可求出S1与S2的比的最大值。
21.【答案】(1)证明:如图,
, , ,
,
,
又 ,
,
,
;
(2)解:在 中, , ,
,
同理, ,
,
,
,
解得 ,
.
【解析】【分析】(1)证明 ,可得 ,根据同角的余角相等可得结论;(2)根据勾股定理先计算 和 的长,根据面积法可得 的长,最后由三角函数定义可得结论.
22.【答案】(1)解:将A(﹣1,0)、B(3,0)两点代入y=ax2+bx+3得: ,解得:a﹣1,b=2.
∴抛物线的表达式为:y=﹣x2+2x+3
(2)解:由题意设P(x,﹣x2+2x+3),过点P作x轴的垂线,交直线BC于点Q.
将x=0代入抛物线的解析式得:y=3,
∴点C的坐标为(0,3).
设直线BC的解析式为y=kx+b,将点B,C的坐标代入得: ,
解得:k=﹣1,b=3.
∴直线CB解析式:y=﹣x+3,则Q(x,﹣x+3)
∴PQ=﹣x2+2x+3﹣(﹣x+3)=﹣x2+3x.
∴S△BCD= PQ OB= ×(﹣x2+3x)×3=﹣ (x﹣ )2+ .
∴当x= 时,S△BCD取最大值,
此时P( , ).
(3)解:∵抛物线y=﹣(x﹣3)(x+1)=﹣x2+2x+3与与y轴交于点C,
∴C点坐标为(0,3),顶点(1,4),E(1,0)
∴tan∠BDE= = .
①当点M在对称轴的右侧时.
(i)作当点N在射线CD上时,如图2,过点N作y轴的垂线,垂足为G,
过点M作GN的垂线,垂足为H,则△CNG,△MNH均为等腰直角三角形.
∵∠CMN=∠BDE,
∴tan∠CMN=tan∠BDE= = .
∴△CNG,△MNH相似比为1:2
设CG=a,则NG=a,NH=NH=2a,
∴M(3a,3+a﹣2a),即M(3a,3﹣a),
将点M的坐标代入抛物线的解析式得:﹣(3a)2+2×3a+3=3﹣a,解得:a=0(舍去)或a=
此时M( , ).
(ii)若点N在射线DC上,如图3,过点N作x轴的垂线l,分别过点M、C作GN的垂线,垂足为H、G,则△CNG,△MNH均为等腰直角三角形,
∵∠CMN=∠BDE,
∴tan∠CMN=tan∠BDE= = ,
∴△CNG与△MNH相似比为1:2
设CG=a,则NG=a,NH=NH=2a,
∴M(a,3﹣a﹣2a),即M(a,3﹣3a),
将点M的坐标代入抛物线的解析式得:﹣a2+2a+3=3﹣3a,解得:a=0(舍去)或a=5,此时M(5,12)
②当点M在对称轴左侧时.
∵∠CMN=∠BDE<45°,
∴∠MCN>45°,
∵抛物线左侧任意一点K,都有∠KCN<45°,
∴点M不存在.
综上可知,点M坐标为( , )或(5,12)
【解析】【分析】(1)将A(﹣1,0)、B(3,0)两点代入得到关于a、b的方程组,可求得a、b的值;(2)由题意设P(x,﹣x2+2x+3),过点P作x轴的垂线,交直线BC于点Q.先求得直线BC的解析式,则得到Q(x,﹣x+3),然后列出△BCD的面积与x的关系式,利用配方法可求得点P的横坐标以及△CBD的面积的最大值;(3)首先求得C点坐标为(0,3),顶点(1,4),E(1,0)则tan∠BDE= .①当点M在对称轴的右侧时,作当点N在射线CD上时,如图1,过点N作y轴的垂线,垂足为G,过点M作GN的垂线,垂足为H,则△CNG,△MNH均为等腰直角三角形.设CG=a,用含a的式子表示点M的坐标,然后将点M的坐标代入抛物线的解析式可求得a的值;若点N在射线DC上,如图,过点N作x轴的垂线l,分别过点M、C作GN的垂线,垂足为H、G,则△CNG,△MNH均为等腰直角三角形,同理可求得此时a的值;②当点M在对称轴左侧时,抛物线左侧任意一点K,都有∠KCN<45°.
