第12 整式的乘除单元达标测试卷(含答案)2023-2024学年华东师大版八年级数学上册
文档属性
| 名称 | 第12 整式的乘除单元达标测试卷(含答案)2023-2024学年华东师大版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 148.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 10:53:20 | ||
图片预览



文档简介
华东师大版八年级数学上册第12 整式的乘除的单元标测试卷
一、单选题
1.下列从左到右的变形中,是因式分解的是( )
A.3xy2=3x·y·y B.x2+2x+2=x(x+2)+2
C.a2-4=(a+2)(a-2) D.(x+3)2=x2+6x+9
2.2014 湖州)计算2x(3x2+1),正确的结果是( )
A.5x3+2x B.6x3+1 C.6x3+2x D.6x2+2x
3.的计算结果是( )
A.x5 B.x6 C.x8 D.x9
4.下列计算结果正确的是( )
A.a3×a4=a12 B.a5÷a=a5
C.(ab2)3=ab6 D.(a3)2=a6
5.计算(﹣ xy2)3,结果正确的是( )
A. x3y5 B.﹣ x3y6 C. x3y6 D.﹣ x3y5
6.若 ,那么 的值分别是( )
A.m=1,n=3 B.m=4,n=5 C.m=2,n=-3 D.m=-2 ,n=3
7.下列运算正确的是( )
A.m2+2m3=3m5 B.(m2)3=m6 C.m2 m3=m6 D.(mn)3=mn3
8.若a﹣b=5,ab=﹣6,则a2﹣3ab+b2的值为( )
A.13 B.19 C.25 D.31
9.下列四个等式:① ,② ,③ ,④ ,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
10.计算:(a-b)(a+b)(a2+b2)(a4+b4)的结果是( )
A.a8+2a4b4+b8 B.a8-2a4b4+b8
C.a8+b8 D.a8-b8
二、填空题
11.已知a+b=8,a﹣b=4,则a2﹣b2= .
12.(2x6﹣3x5+4x4﹣7x3+2x﹣5)(3x5﹣3x3+2x2+3x﹣8)展开式中x8的系数是 .
13.计算: .
14.若 是一个完全平方公式,则k= .
三、计算题
15.计算:
(1)(x﹣y)(x2+xy+y2)
(2) .
16.因式分解:
(1)
(2)
四、解答题
17.已知5x=36,5y=2,求5x﹣2y的值.
18.已知(a+b)2=16,ab=4,求a2+b2与(a-b)2的值.
19.已知a,b,c为△ABC的三条边的长,当b2+2ab=c2+2ac时,
(1)试判断△ABC属于哪一类三角形;
(2)若a=4,b=3,求△ABC的周长.
20.如图所示的是某居民小区的一块长为bm,宽为2am的长方形空地,为了美化环境,准备在这个长方形空地的四个顶点各修建一个半径为am的扇形花台,然后在花台内种花,其余空地种草,如果建筑花台及种花每平方米需要资金200元,种草每平方米需要资金150元,那么美化这块空地共需资金多少元?
五、综合题
21.乘法公式的探究及应用:
(1)如图,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式: (用式子表达);
(4)运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)
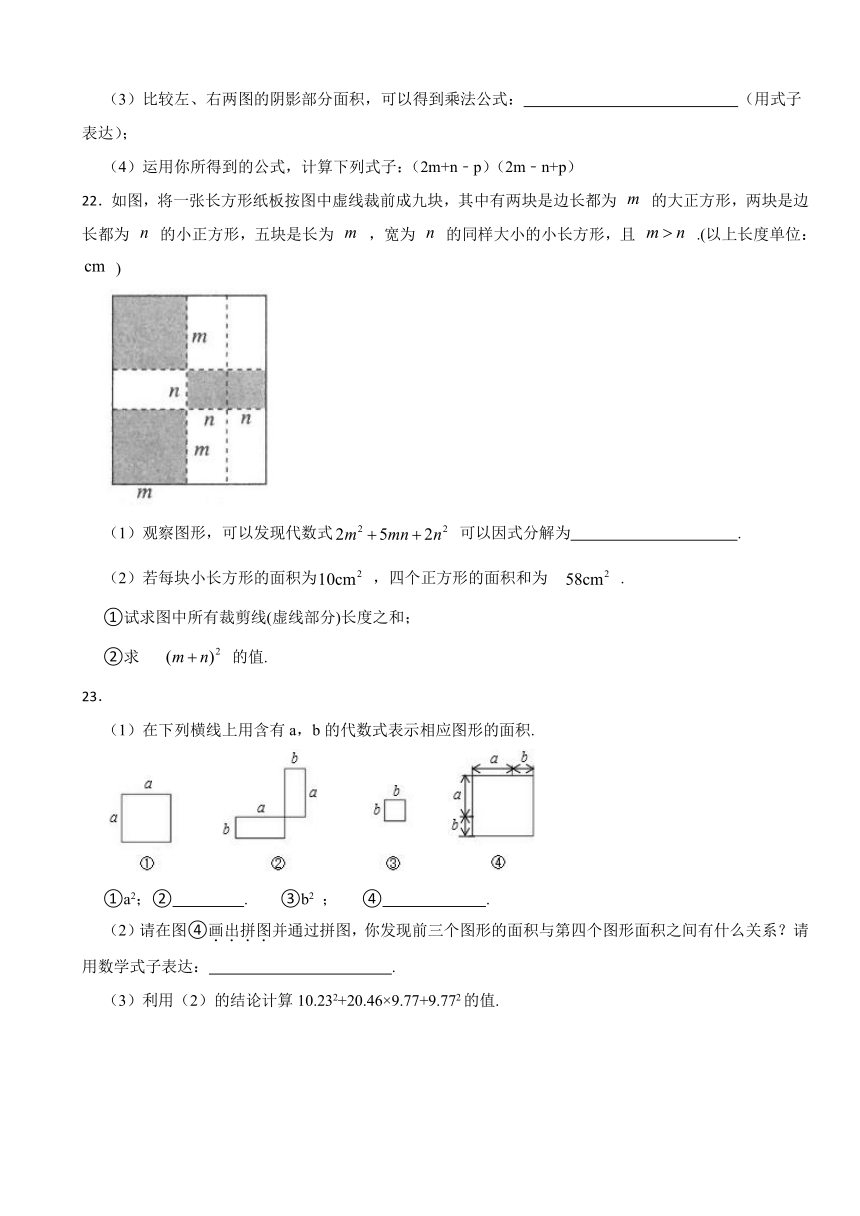
22.如图,将一张长方形纸板按图中虚线裁前成九块,其中有两块是边长都为 的大正方形,两块是边长都为 的小正方形,五块是长为 ,宽为 的同样大小的小长方形,且 .(以上长度单位: )
(1)观察图形,可以发现代数式 可以因式分解为 .
(2)若每块小长方形的面积为 ,四个正方形的面积和为 .
①试求图中所有裁剪线(虚线部分)长度之和;
②求 的值.
23.
(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
①a2;② . ③b2 ; ④ .
(2)请在图④画出拼图并通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表达: .
(3)利用(2)的结论计算10.232+20.46×9.77+9.772的值.
答案解析部分
1.【答案】C
2.【答案】C
【解析】【解答】解:原式=6x3+2x,
故选:C.
【分析】原式利用单项式乘以多项式法则计算即可得到结果.
3.【答案】A
【解析】【分析】根据同底数幂的乘法法则即可得到结果。
【解答】=,故选A.
【点评】解答本题的关键是熟练掌握同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加。
4.【答案】D
【解析】【解答】解:A、a3×a4=a7,故此选项错误;
B、a5÷a=a4,故此选项错误;
C、(ab2)3=a3b6,故此选项错误;
D、(a3)2=a6,正确.
故答案为:D.
【分析】利用同底数幂的乘除运算法则、积的乘方运算法则分别计算得出答案.
5.【答案】B
【解析】【解答】解:原式=﹣( )3x3y6=﹣ x3y6.
故答案为:B.
【分析】积的乘方即对积的每一个因式进行乘方的运算.
6.【答案】C
【解析】【解答】解:利用多项式乘法公式 得到 ,
所以 ,
所以C为正确答案.
故答案为:C.
【分析】根据多项式与多项式相乘法即可得到答案,注意:运用多项式乘法法则必须做到不重不漏,按“同号得正,异号得负”确定积中每项的符号.
7.【答案】B
【解析】【解答】解:A、m2和2m3不是同类项,不能合并,∴m2+2m3≠3m5,不符合题意;
B、(m2)3=m6, 符合题意;
C、 m2 m3=m2+3=m5, 不符合题意;
D、 (mn)3=m3n3,不符合题意;
故答案为:B.
【分析】只有同类项才能相加减;幂的乘方,底数不变,指数相乘;同底数幂相乘底数不变,指数相加;积的乘方等于乘方的积。根据法则计算判断即可。
8.【答案】D
【解析】【解答】解:∵a﹣b=5,ab=﹣6,
∴a2﹣3ab+b2=(a﹣b)2﹣ab=52﹣(﹣6)=31.
故答案为:D.
【分析】利用完全平方公式可将待求式变形为(a-b)2-ab,然后将已知条件代入进行计算.
9.【答案】A
【解析】【解答】①(3x)3=27x3,不符合题意;②(x+y)(-x-y)=-x2-y2-2xy,不符合题意;③4m2-n2=(2m+n)(2m-n),不符合题意;④(-a-b)2=a2+2ab+b2,符合题意,
其中正确的个数是1个.
故答案为:A.
【分析】各项计算得到结果,即可做出判断.
10.【答案】D
【解析】【解答】根据平方差公式可直接求解,即原式=( )( )( )=( )( )= .
故答案为:D
【分析】利用平方差公式从左到右,依次计算即可.
11.【答案】32
【解析】【解答】解:∵a+b=8,a﹣b=4,
∴a2﹣b2=(a+b)(a﹣b)=8×4=32,
故答案为:32.
【分析】先根据平方差公式变形,再代入求出即可.
12.【答案】﹣8
【解析】【解答】∵(2x6﹣3x5+4x4﹣7x3+2x﹣5)(3x5﹣3x3+2x2+3x﹣8)展开式中含x8的项可以由2x6与2x2、﹣3x5与﹣3x3、﹣7x3与3x5相乘得
∴展开式中含x8项分别为:4x8、9x8、﹣21x8
∴展开式中x8的系数是:4+9﹣21=13﹣21=﹣8.
故答案为:﹣8.
【分析】本题主要考查多项式乘以多项式的法则,注意运用简便方法.
根据多项式乘以多项式的法则可知展开式中含x8的项可以由2x6与2x2、﹣3x5与﹣3x3、﹣7x3与3x5相乘得,故可直接将几式相乘后再相加即可得出系数.
13.【答案】
【解析】【解答】解:(x+1)(x-1)=x2-1.
故答案为 .
【分析】利用平方差公式计算求解即可。
14.【答案】
【解析】【解答】解:∵(3k±1)2=9x2+kx+1
∴k=±6
【分析】根据完全平方公式的含义即可得到k的值。
15.【答案】(1)解:(1)原式=x3+x2y+xy2﹣x2y﹣xy2﹣y3
=x3﹣y3;
(2)解:原式=36x4y2 ( x3y2﹣ x2y+x)
=12x7y4﹣8x6y3+36x5y2.
【解析】【分析】(1)根据多项式乘以多项式法则进行计算,再合并同类项即可;(2)先算乘方,再根据单项式乘以多项式法则进行计算即可.
16.【答案】(1)解:原式=
=
(2)解:原式=
=
【解析】【分析】(1)首先提取公因式3x,然后利用平方差公式进行分解;
(2)首先提取公因式a,然后利用完全平方公式进行分解.
17.【答案】解:(5y)2=52y=4,
5x﹣2y=5x÷52y
=36÷4
=9
【解析】【分析】根据同底数幂的除法底数不变指数相减,可得答案.
18.【答案】解:
a2+b2=(a+b)2-2ab=16-2×4=8;
(a-b)2=(a+b)2-4ab=16-4×4=0.
【解析】【解答】
a2+b2=(a+b)2-2ab=16-2×4=8;
(a-b)2=(a+b)2-4ab=16-4×4=0.
【分析】充分了解和的完全平方与差的完全平方之间的关系是本题的关键.
19.【答案】解:(1)△ABC是等腰三角形,理由如下:
∵a,b,c为△ABC的三条边的长,b2+2ab=c2+2ac,
∴b2﹣c2+2ab﹣2ac=0,
因式分解得:(b﹣c)(b+c+2a)=0,
∴b﹣c=0,
∴b=c,
∴△ABC是等腰三角形;
(2)∵a=4,b=3,
∴b=c=3,
∴△ABC的周长=a+b+c=4+3+3=10.
【解析】【分析】(1)由已知条件得出b2﹣c2+2ab﹣2ac=0,用分组分解法进行因式分解得出(b﹣c)(b+c+2a)=0,得出b﹣c=0,因此b=c,即可得出结论;
(2)由(1)得出b=c=3,即可求出△ABC的周长.
20.【答案】解:长方形空地的面积为:2a×b=2ab(m2),四个半径为am的扇形花台的面积为:4 πa2(m2),中间阴影多边形的面积为2ab﹣πa2=a(2b﹣πa)m2
所以美化这块空地共需资金:200×πa2+150×a(2b﹣πa)
=200πa2+300ab﹣150πa2
=300ab+50πa2.
答:美化这块空地共需资金(300ab+50πa2)元.
【解析】【分析】先计算矩形面积、四个扇形的面积以及中间种草的多边形的面积,根据不同造价计算出这块空地共需要的资金.
21.【答案】(1)a2﹣b2
(2)a﹣b;a+b;(a+b)(a﹣b)
(3)(a+b)(a﹣b)=a2﹣b2
(4)解:(2m+n﹣p)(2m﹣n+p)
=(2m)2﹣(n﹣p)2
=4m2﹣(n2﹣2np+p2)
=4m2﹣n2+2np﹣p2.
【解析】【解答】(1)由图可得,阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;(2)由图可得,矩形的宽是a﹣b,长是a+b,面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);(3)依据两图的阴影部分面积相等,可以得到乘法公式(a+b)(a﹣b)=a2﹣b2;
故答案为:(a+b)(a﹣b)=a2﹣b2;
【分析】(1)阴影部分的面积=以a为边长的正方形的面积-以b为边长的正方形的面积;
(2)由拼接的图形知两部分的宽相等,根据剪切可知宽为a-b,长为a+b,面积=长×宽;
(3)将(1)和(2)的面积用等号连接即可;
(4)参考(3)所得的公式计算即可。
22.【答案】(1)(m+2n)(2m+n)
(2)解:依题意,得 .
∴
∵
∴
∵ ,
∴ .
①裁剪线长为2(2m+n)+2(m+2n)=6m+6n=-42,
图中所有裁剪线(虚线部分)长度之和为42cm.
②(m+n)2=49.
【解析】
【分析】(1)图中长方形的面积恒定不变,结合图中长方形面积公式即可把原式进行因式分解;(2)根据题意得出2m2+2n2=58,mn=10,利用完全平方公式得出m+n=7,①根据图中所有裁剪线(虚线部分)长度之和为6(m+n),即可得出答案;②根据m+n=7,即可得出(m+n)2=49.
23.【答案】(1)2ab;(a+b)2
(2)a2+2ab+b2=(a+b)2
(3)10.232+20.46×9.77+9.772=(19+1)2=400.
【解析】【解答】解:(1)a2、2ab、b2、(a+b)2;
故答案为:2ab,(a+b)2;
(2)如图:
a2+2ab+b2=(a+b)2;
故答案为:a2+2ab+b2=(a+b)2;
【分析】(1)根据矩形、正方形的面积公式进行解答;
(2)根据面积之间的和差关系可得a2+2ab+b2=(a+b)2;
(3)原式可变形为(10.23+9.77)2,据此计算.
一、单选题
1.下列从左到右的变形中,是因式分解的是( )
A.3xy2=3x·y·y B.x2+2x+2=x(x+2)+2
C.a2-4=(a+2)(a-2) D.(x+3)2=x2+6x+9
2.2014 湖州)计算2x(3x2+1),正确的结果是( )
A.5x3+2x B.6x3+1 C.6x3+2x D.6x2+2x
3.的计算结果是( )
A.x5 B.x6 C.x8 D.x9
4.下列计算结果正确的是( )
A.a3×a4=a12 B.a5÷a=a5
C.(ab2)3=ab6 D.(a3)2=a6
5.计算(﹣ xy2)3,结果正确的是( )
A. x3y5 B.﹣ x3y6 C. x3y6 D.﹣ x3y5
6.若 ,那么 的值分别是( )
A.m=1,n=3 B.m=4,n=5 C.m=2,n=-3 D.m=-2 ,n=3
7.下列运算正确的是( )
A.m2+2m3=3m5 B.(m2)3=m6 C.m2 m3=m6 D.(mn)3=mn3
8.若a﹣b=5,ab=﹣6,则a2﹣3ab+b2的值为( )
A.13 B.19 C.25 D.31
9.下列四个等式:① ,② ,③ ,④ ,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
10.计算:(a-b)(a+b)(a2+b2)(a4+b4)的结果是( )
A.a8+2a4b4+b8 B.a8-2a4b4+b8
C.a8+b8 D.a8-b8
二、填空题
11.已知a+b=8,a﹣b=4,则a2﹣b2= .
12.(2x6﹣3x5+4x4﹣7x3+2x﹣5)(3x5﹣3x3+2x2+3x﹣8)展开式中x8的系数是 .
13.计算: .
14.若 是一个完全平方公式,则k= .
三、计算题
15.计算:
(1)(x﹣y)(x2+xy+y2)
(2) .
16.因式分解:
(1)
(2)
四、解答题
17.已知5x=36,5y=2,求5x﹣2y的值.
18.已知(a+b)2=16,ab=4,求a2+b2与(a-b)2的值.
19.已知a,b,c为△ABC的三条边的长,当b2+2ab=c2+2ac时,
(1)试判断△ABC属于哪一类三角形;
(2)若a=4,b=3,求△ABC的周长.
20.如图所示的是某居民小区的一块长为bm,宽为2am的长方形空地,为了美化环境,准备在这个长方形空地的四个顶点各修建一个半径为am的扇形花台,然后在花台内种花,其余空地种草,如果建筑花台及种花每平方米需要资金200元,种草每平方米需要资金150元,那么美化这块空地共需资金多少元?
五、综合题
21.乘法公式的探究及应用:
(1)如图,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式: (用式子表达);
(4)运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)
22.如图,将一张长方形纸板按图中虚线裁前成九块,其中有两块是边长都为 的大正方形,两块是边长都为 的小正方形,五块是长为 ,宽为 的同样大小的小长方形,且 .(以上长度单位: )
(1)观察图形,可以发现代数式 可以因式分解为 .
(2)若每块小长方形的面积为 ,四个正方形的面积和为 .
①试求图中所有裁剪线(虚线部分)长度之和;
②求 的值.
23.
(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
①a2;② . ③b2 ; ④ .
(2)请在图④画出拼图并通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表达: .
(3)利用(2)的结论计算10.232+20.46×9.77+9.772的值.
答案解析部分
1.【答案】C
2.【答案】C
【解析】【解答】解:原式=6x3+2x,
故选:C.
【分析】原式利用单项式乘以多项式法则计算即可得到结果.
3.【答案】A
【解析】【分析】根据同底数幂的乘法法则即可得到结果。
【解答】=,故选A.
【点评】解答本题的关键是熟练掌握同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加。
4.【答案】D
【解析】【解答】解:A、a3×a4=a7,故此选项错误;
B、a5÷a=a4,故此选项错误;
C、(ab2)3=a3b6,故此选项错误;
D、(a3)2=a6,正确.
故答案为:D.
【分析】利用同底数幂的乘除运算法则、积的乘方运算法则分别计算得出答案.
5.【答案】B
【解析】【解答】解:原式=﹣( )3x3y6=﹣ x3y6.
故答案为:B.
【分析】积的乘方即对积的每一个因式进行乘方的运算.
6.【答案】C
【解析】【解答】解:利用多项式乘法公式 得到 ,
所以 ,
所以C为正确答案.
故答案为:C.
【分析】根据多项式与多项式相乘法即可得到答案,注意:运用多项式乘法法则必须做到不重不漏,按“同号得正,异号得负”确定积中每项的符号.
7.【答案】B
【解析】【解答】解:A、m2和2m3不是同类项,不能合并,∴m2+2m3≠3m5,不符合题意;
B、(m2)3=m6, 符合题意;
C、 m2 m3=m2+3=m5, 不符合题意;
D、 (mn)3=m3n3,不符合题意;
故答案为:B.
【分析】只有同类项才能相加减;幂的乘方,底数不变,指数相乘;同底数幂相乘底数不变,指数相加;积的乘方等于乘方的积。根据法则计算判断即可。
8.【答案】D
【解析】【解答】解:∵a﹣b=5,ab=﹣6,
∴a2﹣3ab+b2=(a﹣b)2﹣ab=52﹣(﹣6)=31.
故答案为:D.
【分析】利用完全平方公式可将待求式变形为(a-b)2-ab,然后将已知条件代入进行计算.
9.【答案】A
【解析】【解答】①(3x)3=27x3,不符合题意;②(x+y)(-x-y)=-x2-y2-2xy,不符合题意;③4m2-n2=(2m+n)(2m-n),不符合题意;④(-a-b)2=a2+2ab+b2,符合题意,
其中正确的个数是1个.
故答案为:A.
【分析】各项计算得到结果,即可做出判断.
10.【答案】D
【解析】【解答】根据平方差公式可直接求解,即原式=( )( )( )=( )( )= .
故答案为:D
【分析】利用平方差公式从左到右,依次计算即可.
11.【答案】32
【解析】【解答】解:∵a+b=8,a﹣b=4,
∴a2﹣b2=(a+b)(a﹣b)=8×4=32,
故答案为:32.
【分析】先根据平方差公式变形,再代入求出即可.
12.【答案】﹣8
【解析】【解答】∵(2x6﹣3x5+4x4﹣7x3+2x﹣5)(3x5﹣3x3+2x2+3x﹣8)展开式中含x8的项可以由2x6与2x2、﹣3x5与﹣3x3、﹣7x3与3x5相乘得
∴展开式中含x8项分别为:4x8、9x8、﹣21x8
∴展开式中x8的系数是:4+9﹣21=13﹣21=﹣8.
故答案为:﹣8.
【分析】本题主要考查多项式乘以多项式的法则,注意运用简便方法.
根据多项式乘以多项式的法则可知展开式中含x8的项可以由2x6与2x2、﹣3x5与﹣3x3、﹣7x3与3x5相乘得,故可直接将几式相乘后再相加即可得出系数.
13.【答案】
【解析】【解答】解:(x+1)(x-1)=x2-1.
故答案为 .
【分析】利用平方差公式计算求解即可。
14.【答案】
【解析】【解答】解:∵(3k±1)2=9x2+kx+1
∴k=±6
【分析】根据完全平方公式的含义即可得到k的值。
15.【答案】(1)解:(1)原式=x3+x2y+xy2﹣x2y﹣xy2﹣y3
=x3﹣y3;
(2)解:原式=36x4y2 ( x3y2﹣ x2y+x)
=12x7y4﹣8x6y3+36x5y2.
【解析】【分析】(1)根据多项式乘以多项式法则进行计算,再合并同类项即可;(2)先算乘方,再根据单项式乘以多项式法则进行计算即可.
16.【答案】(1)解:原式=
=
(2)解:原式=
=
【解析】【分析】(1)首先提取公因式3x,然后利用平方差公式进行分解;
(2)首先提取公因式a,然后利用完全平方公式进行分解.
17.【答案】解:(5y)2=52y=4,
5x﹣2y=5x÷52y
=36÷4
=9
【解析】【分析】根据同底数幂的除法底数不变指数相减,可得答案.
18.【答案】解:
a2+b2=(a+b)2-2ab=16-2×4=8;
(a-b)2=(a+b)2-4ab=16-4×4=0.
【解析】【解答】
a2+b2=(a+b)2-2ab=16-2×4=8;
(a-b)2=(a+b)2-4ab=16-4×4=0.
【分析】充分了解和的完全平方与差的完全平方之间的关系是本题的关键.
19.【答案】解:(1)△ABC是等腰三角形,理由如下:
∵a,b,c为△ABC的三条边的长,b2+2ab=c2+2ac,
∴b2﹣c2+2ab﹣2ac=0,
因式分解得:(b﹣c)(b+c+2a)=0,
∴b﹣c=0,
∴b=c,
∴△ABC是等腰三角形;
(2)∵a=4,b=3,
∴b=c=3,
∴△ABC的周长=a+b+c=4+3+3=10.
【解析】【分析】(1)由已知条件得出b2﹣c2+2ab﹣2ac=0,用分组分解法进行因式分解得出(b﹣c)(b+c+2a)=0,得出b﹣c=0,因此b=c,即可得出结论;
(2)由(1)得出b=c=3,即可求出△ABC的周长.
20.【答案】解:长方形空地的面积为:2a×b=2ab(m2),四个半径为am的扇形花台的面积为:4 πa2(m2),中间阴影多边形的面积为2ab﹣πa2=a(2b﹣πa)m2
所以美化这块空地共需资金:200×πa2+150×a(2b﹣πa)
=200πa2+300ab﹣150πa2
=300ab+50πa2.
答:美化这块空地共需资金(300ab+50πa2)元.
【解析】【分析】先计算矩形面积、四个扇形的面积以及中间种草的多边形的面积,根据不同造价计算出这块空地共需要的资金.
21.【答案】(1)a2﹣b2
(2)a﹣b;a+b;(a+b)(a﹣b)
(3)(a+b)(a﹣b)=a2﹣b2
(4)解:(2m+n﹣p)(2m﹣n+p)
=(2m)2﹣(n﹣p)2
=4m2﹣(n2﹣2np+p2)
=4m2﹣n2+2np﹣p2.
【解析】【解答】(1)由图可得,阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;(2)由图可得,矩形的宽是a﹣b,长是a+b,面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);(3)依据两图的阴影部分面积相等,可以得到乘法公式(a+b)(a﹣b)=a2﹣b2;
故答案为:(a+b)(a﹣b)=a2﹣b2;
【分析】(1)阴影部分的面积=以a为边长的正方形的面积-以b为边长的正方形的面积;
(2)由拼接的图形知两部分的宽相等,根据剪切可知宽为a-b,长为a+b,面积=长×宽;
(3)将(1)和(2)的面积用等号连接即可;
(4)参考(3)所得的公式计算即可。
22.【答案】(1)(m+2n)(2m+n)
(2)解:依题意,得 .
∴
∵
∴
∵ ,
∴ .
①裁剪线长为2(2m+n)+2(m+2n)=6m+6n=-42,
图中所有裁剪线(虚线部分)长度之和为42cm.
②(m+n)2=49.
【解析】
【分析】(1)图中长方形的面积恒定不变,结合图中长方形面积公式即可把原式进行因式分解;(2)根据题意得出2m2+2n2=58,mn=10,利用完全平方公式得出m+n=7,①根据图中所有裁剪线(虚线部分)长度之和为6(m+n),即可得出答案;②根据m+n=7,即可得出(m+n)2=49.
23.【答案】(1)2ab;(a+b)2
(2)a2+2ab+b2=(a+b)2
(3)10.232+20.46×9.77+9.772=(19+1)2=400.
【解析】【解答】解:(1)a2、2ab、b2、(a+b)2;
故答案为:2ab,(a+b)2;
(2)如图:
a2+2ab+b2=(a+b)2;
故答案为:a2+2ab+b2=(a+b)2;
【分析】(1)根据矩形、正方形的面积公式进行解答;
(2)根据面积之间的和差关系可得a2+2ab+b2=(a+b)2;
(3)原式可变形为(10.23+9.77)2,据此计算.
