1.3 集合的基本运算 课件(共26张PPT)
文档属性
| 名称 | 1.3 集合的基本运算 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 517.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 10:00:39 | ||
图片预览








文档简介
(共26张PPT)
集合的基本运算(2)
(2 ) 在有理数范围内解方程:(x - 2) (x2 - 3) = 0.
(1 ) 在实数范围内解方程:(x - 2) (x2 - 3) = 0.
复习引入
高中数学
(1 ) 在实数范围内解方程:(x - 2) (x2 - 3) = 0.
{x R (x - 2) (x2 - 3) = 0} = {2, , - }
(2 ) 在有理数范围内解方程:(x - 2) (x2 - 3) = 0. {x Q (x - 2) (x2 - 3) = 0} = {2}
高中数学
复习引入
(1 ) 在实数范围内解方程:(x - 2) (x2 - 3) = 0.
{x R (x - 2) (x2 - 3) = 0} = {2, , - }
(2 ) 在有理数范围内解方程:(x - 2) (x2 - 3) = 0. {x Q (x - 2) (x2 - 3) = 0} = {2}
方程相同,为什么结果不同?
高中数学
复习引入
R
2 -
(1 ) 在实数范围内解方程:(x - 2) (x2 - 3) = 0.
( ) ( )
(2 ) 在有理数范围内解方程:(x - 2) (x2 - 3) = 0.
{x Q (x - 2) (x2 - 3) = 0} = {2}
高中数学
2
Q
{ }
2 { }
x R x - 2 x - 3 = 0 = 2, 3, - 3
复习引入
1. 全集的概念
一般地, 如果 一 个集合含有所研究问题中涉及的 所有元
素, 那么就称这个集合为全集, 记作 U .
2
Q
2 -
R
A
U
概念的理解
高中数学
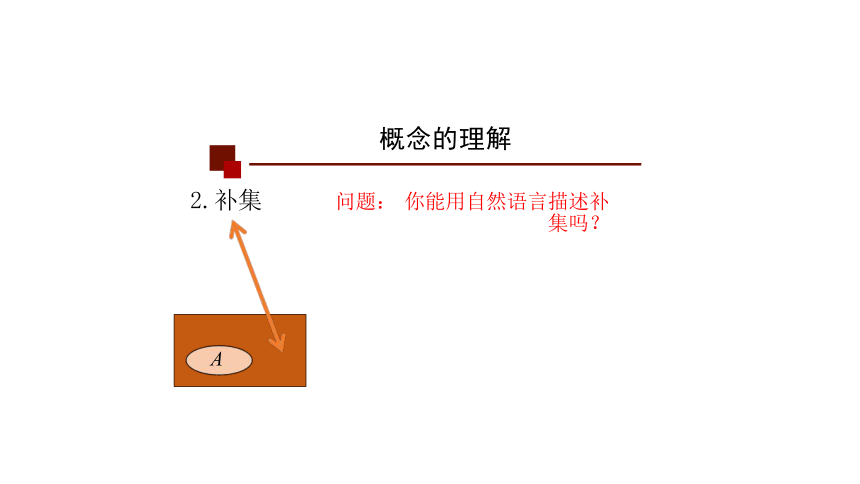
2.补集 问题: 你能用自然语言描述补集吗?
概念的理解
高中数学
A
2.补集的概念
对于 一 个集合A, 由全集 U 中不属于集合A的所有元素组
U
成的集合, 称为集合 A相对于全集U
的补集.记作: UA.
概念的理解
A
高中数学
A
2.补集的概念
对于 一 个集合A, 由全集 U 中不属于集合A的所有元素组 成的集合, 称为集合 A相对于全集U 的补集.记作: UA.
U
问题: 你能用符号语言表示补集吗?
概念的理解
A
高中数学
A
2.补集的概念
对于 一 个集合A, 由全集 U 中不属于集合A的所有元素组 成的集合, 称为集合 A相对于全集U 的补集.记作: UA.
问题: 你能用符号语言表示补集吗?
U A = {x x U , 且 x A}
U
概念的理解
A
高中数学
A
U = {x x 是小于9的正整数 , A=〈 1,2,3 〉, B =〈 3,4,5,6 〉,
求gUA , gU B , AngU B , (||( A n(||( B .
J
)
l
(
J
)
l
(
例 1:设
概念的巩固练习
高中数学
U A = {4, 5, 6, 7, 8}, (痧UA)n ( UB) = {7, 8}.
UB = {1, 2, 7, 8},
高中数学
求gUA , gU B , AngU B , (||(gUA n(||(gUB .
解: U = {1, 2, 3, 4, 5, 6, 7, 8},
例 1:设
|
〉|
)
J
U ={x x 是小于9的正整数
, A=〈 1,2,3 〉, B =〈 3,4,5,6 〉,
J
)
l
(
J
)
l
(
An UB = {1, 2},
概念的巩固练习
例 2 : 设 全 集 U = {x x 是三角形 , A=〈 x x是锐角三角形 |〉,
B =〈 x x是钝角三角形 |〉,求An B, gU (|(AUB .
解: An B = ,
A UB = {x x 是锐角三角形或钝角三角形}, U (A UB) = {x 是直角三角形}.
高中数学
概念的巩固练习
例 3: 已知集合A=〈 x 3 x<7 , B =〈 x 2< x<10 ,求gR (|(AUB , gR (|(AnB , (||(gRA nB , AU(||(gRB .
解:
AUB =〈(x 2 R (A UB) = {x x 2或x 10}. 0 2 3 7 10 x
l
(
l J
概念的巩固练习
高中数学
例 3: 已知集合A=〈 x 3 x<7 , B =〈 x 2< x<10 ,求gR (|(AUB ,
gR (|(AnB , (||(gRA nB , AU(||(gRB .
解:
x 7}. 0 2 0 x
高中数学
或
,
l
(
概念的巩固练习
解:
B } 或7 < 0 .
高中数学
1
7
x
0 x
x
0
3
,
x
2
或
x
3
n
{
( RA
RA
例 3: 已知集合A=〈 x 3 x<7 , B =〈 x 2< x<10 ,求gR (|(AUB ,
gR (|(AnB , (||(gRA nB , AU(||(gRB .
l
(
概念的巩固练习
AU ( RB ) = {x x 2或3 x < 7或x 10}.
高中数学
例 3: 已知集合A=〈 x 3 x<7 ,
gR (|(AnB , (||(gRA nB , AU(||(gRB .
解:
RB = {x x 2或x 10},
2< x<10 ,求gR (|(AUB ,
概念的巩固练习
0 2 3 7 10 x
B =〈(|x
|l
例 3: 已知集合A=〈 x 3< x<7 , B =〈 x 2< x<10 ,求gR (|(AUB ,
gR (|(AnB , (||(gRA nB , AU(||(gRB .
l
(
0 2 3 7 10 x 0 2 3
问题: 怎样才能增强条件的直观性呢?
0 2 3 7 10 x 0 2 3 7 10 x
概念的巩固练习
高中数学
7 10
x
例 3: 已知集合A=〈 x 3< x<7 , B =〈 x 2< x<10 ,求gR (|(AUB ,
gR (|(AnB , (||(gRA nB , AU(||(gRB .
l
(
0 2 3 7 10 x 0 2 3 7 10
问题: 怎样才能增强条件的直观性呢?
连续数集—— 数轴
0 2 3 7 10 x 0 2 3 7 10 x
概念的巩固练习
高中数学
x
(2) (||( A U(||( B .
U A
B
B
(1) (||( A n(||( B ;
U A
例 4: 图中U是全集 , A,B是U的两个子集 , 用阴影表示:
概念的巩固练习
高中数学
A B
A B
A B
A B
例 4: 图中U是全集 , A,B是U的两个子集 , 用阴影表示:
(痧UA)n ( UB ) = U (A UB)
(1) (||( A n(||( B ;
你能用符号语言表达这个结果吗?
概念的巩固练习
高中数学
解:
A B
例 4: 图中U是全集 , A,B是U的两个子集 , 用阴影表示:
(2) (||( A U(||( B 你能用符号语言表达这个结果吗?
A B
A B
(痧UA)U ( UB ) = U (An B)
(痧UA)n ( UB) = U (A UB)
(痧UA)U ( UB) = U (An B)
概念的巩固练习
高中数学
A B
解:
问题: 怎样增强条件的直观性呢?
高中数学
U A
B
(1) (||(gUA n(||(gUB ; ( 2) (||(gUA U(||(gUB .
例 4: 图中U是全集 , A,B 是U的两个子集 , 用阴影表示:
概念的巩固练习
U A
B
U A
B
U A
B
(1) (||(gUA n(||(gUB ; ( 2) (||(gUA U(||(gUB .
例 4: 图中U是全集 , A,B 是U的两个子集 , 用阴影表示:
抽象集合—— 韦恩图
问题: 怎样增强条件的直观性呢?
概念的巩固练习
高中数学
1.补集的概念:
UA U A = {x x U , 且 x A}
2. 方法反思: 连续数集可运用数轴增强直观性, 抽象集合或关系较为复杂, 可运用韦恩图的表 示方法.
高中数学
归纳总结
A
作业:
1. 教科书 13页 第1, 2题;
2. 课后练习.
布置作业
高中数学
集合的基本运算(2)
(2 ) 在有理数范围内解方程:(x - 2) (x2 - 3) = 0.
(1 ) 在实数范围内解方程:(x - 2) (x2 - 3) = 0.
复习引入
高中数学
(1 ) 在实数范围内解方程:(x - 2) (x2 - 3) = 0.
{x R (x - 2) (x2 - 3) = 0} = {2, , - }
(2 ) 在有理数范围内解方程:(x - 2) (x2 - 3) = 0. {x Q (x - 2) (x2 - 3) = 0} = {2}
高中数学
复习引入
(1 ) 在实数范围内解方程:(x - 2) (x2 - 3) = 0.
{x R (x - 2) (x2 - 3) = 0} = {2, , - }
(2 ) 在有理数范围内解方程:(x - 2) (x2 - 3) = 0. {x Q (x - 2) (x2 - 3) = 0} = {2}
方程相同,为什么结果不同?
高中数学
复习引入
R
2 -
(1 ) 在实数范围内解方程:(x - 2) (x2 - 3) = 0.
( ) ( )
(2 ) 在有理数范围内解方程:(x - 2) (x2 - 3) = 0.
{x Q (x - 2) (x2 - 3) = 0} = {2}
高中数学
2
Q
{ }
2 { }
x R x - 2 x - 3 = 0 = 2, 3, - 3
复习引入
1. 全集的概念
一般地, 如果 一 个集合含有所研究问题中涉及的 所有元
素, 那么就称这个集合为全集, 记作 U .
2
Q
2 -
R
A
U
概念的理解
高中数学
2.补集 问题: 你能用自然语言描述补集吗?
概念的理解
高中数学
A
2.补集的概念
对于 一 个集合A, 由全集 U 中不属于集合A的所有元素组
U
成的集合, 称为集合 A相对于全集U
的补集.记作: UA.
概念的理解
A
高中数学
A
2.补集的概念
对于 一 个集合A, 由全集 U 中不属于集合A的所有元素组 成的集合, 称为集合 A相对于全集U 的补集.记作: UA.
U
问题: 你能用符号语言表示补集吗?
概念的理解
A
高中数学
A
2.补集的概念
对于 一 个集合A, 由全集 U 中不属于集合A的所有元素组 成的集合, 称为集合 A相对于全集U 的补集.记作: UA.
问题: 你能用符号语言表示补集吗?
U A = {x x U , 且 x A}
U
概念的理解
A
高中数学
A
U = {x x 是小于9的正整数 , A=〈 1,2,3 〉, B =〈 3,4,5,6 〉,
求gUA , gU B , AngU B , (||( A n(||( B .
J
)
l
(
J
)
l
(
例 1:设
概念的巩固练习
高中数学
U A = {4, 5, 6, 7, 8}, (痧UA)n ( UB) = {7, 8}.
UB = {1, 2, 7, 8},
高中数学
求gUA , gU B , AngU B , (||(gUA n(||(gUB .
解: U = {1, 2, 3, 4, 5, 6, 7, 8},
例 1:设
|
〉|
)
J
U ={x x 是小于9的正整数
, A=〈 1,2,3 〉, B =〈 3,4,5,6 〉,
J
)
l
(
J
)
l
(
An UB = {1, 2},
概念的巩固练习
例 2 : 设 全 集 U = {x x 是三角形 , A=〈 x x是锐角三角形 |〉,
B =〈 x x是钝角三角形 |〉,求An B, gU (|(AUB .
解: An B = ,
A UB = {x x 是锐角三角形或钝角三角形}, U (A UB) = {x 是直角三角形}.
高中数学
概念的巩固练习
例 3: 已知集合A=〈 x 3 x<7 , B =〈 x 2< x<10 ,求gR (|(AUB , gR (|(AnB , (||(gRA nB , AU(||(gRB .
解:
AUB =〈(x 2
l
(
l J
概念的巩固练习
高中数学
例 3: 已知集合A=〈 x 3 x<7 , B =〈 x 2< x<10 ,求gR (|(AUB ,
gR (|(AnB , (||(gRA nB , AU(||(gRB .
解:
x 7}. 0 2 0 x
高中数学
或
,
l
(
概念的巩固练习
解:
B } 或7 < 0 .
高中数学
1
7
x
0 x
x
0
3
,
x
2
或
x
3
n
{
( RA
RA
例 3: 已知集合A=〈 x 3 x<7 , B =〈 x 2< x<10 ,求gR (|(AUB ,
gR (|(AnB , (||(gRA nB , AU(||(gRB .
l
(
概念的巩固练习
AU ( RB ) = {x x 2或3 x < 7或x 10}.
高中数学
例 3: 已知集合A=〈 x 3 x<7 ,
gR (|(AnB , (||(gRA nB , AU(||(gRB .
解:
RB = {x x 2或x 10},
2< x<10 ,求gR (|(AUB ,
概念的巩固练习
0 2 3 7 10 x
B =〈(|x
|l
例 3: 已知集合A=〈 x 3< x<7 , B =〈 x 2< x<10 ,求gR (|(AUB ,
gR (|(AnB , (||(gRA nB , AU(||(gRB .
l
(
0 2 3 7 10 x 0 2 3
问题: 怎样才能增强条件的直观性呢?
0 2 3 7 10 x 0 2 3 7 10 x
概念的巩固练习
高中数学
7 10
x
例 3: 已知集合A=〈 x 3< x<7 , B =〈 x 2< x<10 ,求gR (|(AUB ,
gR (|(AnB , (||(gRA nB , AU(||(gRB .
l
(
0 2 3 7 10 x 0 2 3 7 10
问题: 怎样才能增强条件的直观性呢?
连续数集—— 数轴
0 2 3 7 10 x 0 2 3 7 10 x
概念的巩固练习
高中数学
x
(2) (||( A U(||( B .
U A
B
B
(1) (||( A n(||( B ;
U A
例 4: 图中U是全集 , A,B是U的两个子集 , 用阴影表示:
概念的巩固练习
高中数学
A B
A B
A B
A B
例 4: 图中U是全集 , A,B是U的两个子集 , 用阴影表示:
(痧UA)n ( UB ) = U (A UB)
(1) (||( A n(||( B ;
你能用符号语言表达这个结果吗?
概念的巩固练习
高中数学
解:
A B
例 4: 图中U是全集 , A,B是U的两个子集 , 用阴影表示:
(2) (||( A U(||( B 你能用符号语言表达这个结果吗?
A B
A B
(痧UA)U ( UB ) = U (An B)
(痧UA)n ( UB) = U (A UB)
(痧UA)U ( UB) = U (An B)
概念的巩固练习
高中数学
A B
解:
问题: 怎样增强条件的直观性呢?
高中数学
U A
B
(1) (||(gUA n(||(gUB ; ( 2) (||(gUA U(||(gUB .
例 4: 图中U是全集 , A,B 是U的两个子集 , 用阴影表示:
概念的巩固练习
U A
B
U A
B
U A
B
(1) (||(gUA n(||(gUB ; ( 2) (||(gUA U(||(gUB .
例 4: 图中U是全集 , A,B 是U的两个子集 , 用阴影表示:
抽象集合—— 韦恩图
问题: 怎样增强条件的直观性呢?
概念的巩固练习
高中数学
1.补集的概念:
UA U A = {x x U , 且 x A}
2. 方法反思: 连续数集可运用数轴增强直观性, 抽象集合或关系较为复杂, 可运用韦恩图的表 示方法.
高中数学
归纳总结
A
作业:
1. 教科书 13页 第1, 2题;
2. 课后练习.
布置作业
高中数学
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
