指数幂运算 课件(共24张PPT)
文档属性
| 名称 | 指数幂运算 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 501.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 11:31:07 | ||
图片预览





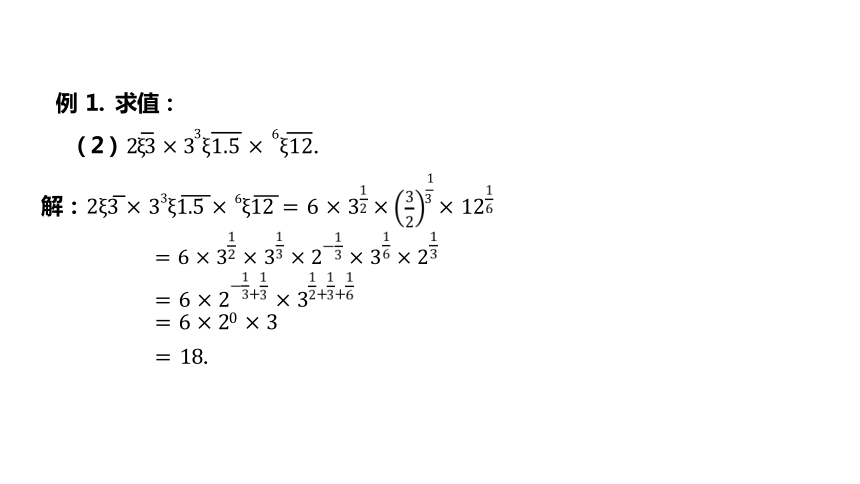



文档简介
(共24张PPT)
指 数 幂 运 算
复习上节课内容:
分数指数幂(有理数指数幂):
a- = nξam , a > 0, m, n ∈ N , n > 1 ;
a - = , a > 0, m, n ∈ N , n > 1 .
n
m
n
m
高中数学
分数指数幂的运算性质:
对于任意的正数a, b ,都有:
① aT aS = aT+S ,
② aT S = aTS , T, S ∈ Q .
③ ab T = aT bT ,
常见形式: = aT a S = aT S .
高中数学
新课:
例 1. 求值:
解 :提示 , 将 1.5化为分数 , 将 化为幂a x 形式.
公式: aT S = aTS .
1.5 = 2 = 3 = .
高中数学
125
216
6
5
2
3
6
5
6
5
3
2
36
25
(1) 1.5;
36
25
1
2ξ3 × 33ξ1.5 × 6ξ12 = 2 × 3 × 3 × 3 × 12 .
= 3 × 2 ,12 = 3 × 22 = 3 × 2
公式: a = nξam ,aT aS = aT +S , = aT S .
高中数学
例 1. 求值:
(2) 2ξ3 × 33ξ1.5 × 6ξ12.
解 :提示 ,将根式化为幂a x 形式.
例 1. 求值:
(2) 2ξ3 × 33ξ1.5 × 6ξ12.
1
解: 2ξ3 × 33ξ1.5 × 6ξ12 = 6 × 3 × 3 × 12
= 6 × 20 × 3
= 18.
= 6 × 3 × 3 × 2 × 3 × 2
= 6 × 2 + × 3 + +
高中数学
总结:
用分数指数幂的形式来表示根式 ,往往会简化根式运算.
运算时尽量化为同底数的幂,即便各项不能都化为相同的底数,也要尽可能地减
少底数的种类.
1
例如: 2ξ3 × 33ξ1.5 × 6ξ12 = 2 × 3 × 3 × 3 × 12
= 2 × 3 × 3 × 3 × 2 × 3 × 2
高中数学
无理数指数幂:
每一个无理数都是一个定值,能够用数轴上的一个点表示. 那么,如
果不用计算器 ,我们如何来估算▽2的值呢?
高中数学
因为12 = 1 < 2 , 所以1 < ξ2;
因为1. 12 = 1.21 < 2 , 所以1 < 1. 1 < ξ2;
因为 11 = 1.2321 < 2 ,所以1 < 1. 1 < 1. 11 < ξ2;
从而产生了一串逐渐向ξ2靠近的数: 1, 1. 1, 1. 11, 1. 111, 我们能否说ξ2 ≈ 1. 11 1? 显然不能!
1.11 1 <1.2<1.3<1.4<ξ2.
高中数学
2
因为1. 12 = 1.21 < 2 , 所以1. 1 < ξ2;
因为1.22 = 1.44 < 2 ,所以1. 1 < 1.2 < ξ2;
因为1.32 = 1.69 < 2 , 所以1. 1 < 1.2 < 1.3 < ξ2;
因为1.42 = 1.69 < 2 ,所以1. 1 < 1.2 < 1.3 < 1.4 < ξ2;
因为1.52 = 2.25 > 2 ,所以1. 1 < 1.2 < 1.3 < 1.4 < ξ2 < 1.5;
问题出在哪里?
高中数学
这列数字逼近ξ2的方式.
一种通用的方式:
值为 1
ξ2且小于ξ2的那一个!
x 的第二个值应该在1.41, 1.42, 1.43, , 1.49中产生,
经试验: 1.412 = 1.9881 < 2 , 1.422 = 2.0164 > 2,
所以x 的第二个值应该是1.41.
高中数学
近
个
接
三
最
第
中
,
数
数
小
小
的
位
数
两
位
为
同
值
在
个
是
二
总
第
x
后
且,
之
而
.4,
次增加一位小数,
,x的第一个值为
,
x
数
数
小
列
位
一
三
设
x 的第三个值应该在1.411, 1.412, 1.413, , 1.419中产生,
经试验: 1.4112 = 1.990921 < 2 ,1.4122 = 1.993744 < 2,
1.4132 = 1.996569 < 2 ,1.4142 = 1.999396 < 2 ,1.4152 = 2.002225 > 2,
所以x的第三个值应该是1.414.
由 ξ 的数x:
3,
近
421
渐逼
1
向
1,
方
42
的
1
2
4
ξ
1
于
42
从
41
列
14, 1
产生一
1 4
能
41
们
1
我
,
,
1 4
此
高中数学
由 ξ 的数x: 而且 , 2 1.96 = 0.04 , 2 1.9881 = 0.0119,
可见它们与ξ2的差是在逐渐缩小趋近于 0 的.
我们将这一串数x 叫做ξ2的不足近似值.
高中数学
3,
近
21
逼
414
逐渐
1
向
1,
方
42
的
1
2
4
ξ
1
于
42
从
41
列
1
一
14,
产生
,1 4
就能
41
们
1
我
,
,
1 4
此
2 1.999396 = 0.000604 , 2 1.99996164 = 0.00003836,
用同样的方法,我们可以制定取ξ2的过剩近似值y的方式:
小数
个!
经由对不足近似值的计算过程 ,我们可以得到一列从大于ξ2的方向逐渐逼近ξ2的数:
1.5 > 1.42 > 1.415 > 1.4143 > 1.41422 > 1.414214 > > ξ2. 这串数字y就是ξ2的过剩近似值.
的那
为三
于ξ2
个值
大
三
且
第
在同位数的小数中最接近ξ
之后第二个值为两位小数
是
5,
总
1.
且,y
个值为
小数,
y的第
位
,
加
于
增
大
次
都
即每
列数y
高中数学
小数位数相同的v2的过剩近似值y与不足近似值x 的差是有规律的:
高中数学
1. 1,
这个差值就是我们常说的ξ2的近似值得精确度 , 如果我们需要一个精确到
0.001 的ξ2的近似值 , 就可以用 1.414.
当ξ2的不足近似值x和过剩近似值y逐渐逼近ξ2时,我们也就得到了精度越来越
高的ξ2的近似值 ,这样一直计算下去 ,我们就可以得到任何精确度的ξ2的近似值.
高中数学
4
1
1.4143 1.4 42 = 0.0001,
高中数学
这个用有理数指数幂逼近无理数指数幂的方法是可以推广的 ,比如2ξ3 , 3π
的值 , 都可以用此方法近似的等于一个有理数指数幂的值.
实数指数幂的运算性质:
对于任意的正数a, b , 都有:
① aT aS = aT +S ,
② aT S = aTS , T, S ∈ R.
③ ab T = aT bT ,
高中数学
例 2. 按从小到大的顺序,可将2ξ3 ,3ξ2 ,π ξ5,2π 重新排列为 (可用
计算工具) .
解: 四个数均为无理数指数幂 ,我们不妨取ξ2, ξ3, ξ5, π 的近似值 ,计算无理数指数幂的近
似值. 不妨精确到 0.001.
ξ2 = 1.414, ξ3 = 1.732, ξ5 = 2.236, π = 3. 142.
2ξ3 = 3.322, 3ξ2 = 4.728, π ξ5 = 12.935, 2π = 8.827.
所以 , 重新排列为2ξ3 , 3ξ2 , 2π , 3ξ5 .
高中数学
总结:
(1)理解由有理数指数幂逼近无理数指数幂的原理;
高中数学
总结:
(2) 实数指数幂的运算性质:
对于任意的a > 0 , b > 0 , T, S ∈ R ,都有:
① aT aS = aT +S ,
② aT S = aTS ,
③ ab T = aT bT ,
高中数学
总结:
(3)用指数幂的形式来表示根式,往往会简化根式运算. 运算时尽量化为同
底数的幂,即便各项不能都化为相同的底数,也要尽可能地减少底数的种类.
高中数学
因为喜欢而学习, 因为通透而热爱!
让我们 一起加油!
高中数学
(l 整数
有理数{l(分数{无 数
实数{无理数: 环小数,例如V2 , V3 , π .
高中数学
无限不循
有理数
限循环小
有限小数
指 数 幂 运 算
复习上节课内容:
分数指数幂(有理数指数幂):
a- = nξam , a > 0, m, n ∈ N , n > 1 ;
a - = , a > 0, m, n ∈ N , n > 1 .
n
m
n
m
高中数学
分数指数幂的运算性质:
对于任意的正数a, b ,都有:
① aT aS = aT+S ,
② aT S = aTS , T, S ∈ Q .
③ ab T = aT bT ,
常见形式: = aT a S = aT S .
高中数学
新课:
例 1. 求值:
解 :提示 , 将 1.5化为分数 , 将 化为幂a x 形式.
公式: aT S = aTS .
1.5 = 2 = 3 = .
高中数学
125
216
6
5
2
3
6
5
6
5
3
2
36
25
(1) 1.5;
36
25
1
2ξ3 × 33ξ1.5 × 6ξ12 = 2 × 3 × 3 × 3 × 12 .
= 3 × 2 ,12 = 3 × 22 = 3 × 2
公式: a = nξam ,aT aS = aT +S , = aT S .
高中数学
例 1. 求值:
(2) 2ξ3 × 33ξ1.5 × 6ξ12.
解 :提示 ,将根式化为幂a x 形式.
例 1. 求值:
(2) 2ξ3 × 33ξ1.5 × 6ξ12.
1
解: 2ξ3 × 33ξ1.5 × 6ξ12 = 6 × 3 × 3 × 12
= 6 × 20 × 3
= 18.
= 6 × 3 × 3 × 2 × 3 × 2
= 6 × 2 + × 3 + +
高中数学
总结:
用分数指数幂的形式来表示根式 ,往往会简化根式运算.
运算时尽量化为同底数的幂,即便各项不能都化为相同的底数,也要尽可能地减
少底数的种类.
1
例如: 2ξ3 × 33ξ1.5 × 6ξ12 = 2 × 3 × 3 × 3 × 12
= 2 × 3 × 3 × 3 × 2 × 3 × 2
高中数学
无理数指数幂:
每一个无理数都是一个定值,能够用数轴上的一个点表示. 那么,如
果不用计算器 ,我们如何来估算▽2的值呢?
高中数学
因为12 = 1 < 2 , 所以1 < ξ2;
因为1. 12 = 1.21 < 2 , 所以1 < 1. 1 < ξ2;
因为 11 = 1.2321 < 2 ,所以1 < 1. 1 < 1. 11 < ξ2;
从而产生了一串逐渐向ξ2靠近的数: 1, 1. 1, 1. 11, 1. 111, 我们能否说ξ2 ≈ 1. 11 1? 显然不能!
1.11 1 <1.2<1.3<1.4<ξ2.
高中数学
2
因为1. 12 = 1.21 < 2 , 所以1. 1 < ξ2;
因为1.22 = 1.44 < 2 ,所以1. 1 < 1.2 < ξ2;
因为1.32 = 1.69 < 2 , 所以1. 1 < 1.2 < 1.3 < ξ2;
因为1.42 = 1.69 < 2 ,所以1. 1 < 1.2 < 1.3 < 1.4 < ξ2;
因为1.52 = 2.25 > 2 ,所以1. 1 < 1.2 < 1.3 < 1.4 < ξ2 < 1.5;
问题出在哪里?
高中数学
这列数字逼近ξ2的方式.
一种通用的方式:
值为 1
ξ2且小于ξ2的那一个!
x 的第二个值应该在1.41, 1.42, 1.43, , 1.49中产生,
经试验: 1.412 = 1.9881 < 2 , 1.422 = 2.0164 > 2,
所以x 的第二个值应该是1.41.
高中数学
近
个
接
三
最
第
中
,
数
数
小
小
的
位
数
两
位
为
同
值
在
个
是
二
总
第
x
后
且,
之
而
.4,
次增加一位小数,
,x的第一个值为
,
x
数
数
小
列
位
一
三
设
x 的第三个值应该在1.411, 1.412, 1.413, , 1.419中产生,
经试验: 1.4112 = 1.990921 < 2 ,1.4122 = 1.993744 < 2,
1.4132 = 1.996569 < 2 ,1.4142 = 1.999396 < 2 ,1.4152 = 2.002225 > 2,
所以x的第三个值应该是1.414.
由 ξ 的数x:
3,
近
421
渐逼
1
向
1,
方
42
的
1
2
4
ξ
1
于
42
从
41
列
14, 1
产生一
1 4
能
41
们
1
我
,
,
1 4
此
高中数学
由 ξ 的数x: 而且 , 2 1.96 = 0.04 , 2 1.9881 = 0.0119,
可见它们与ξ2的差是在逐渐缩小趋近于 0 的.
我们将这一串数x 叫做ξ2的不足近似值.
高中数学
3,
近
21
逼
414
逐渐
1
向
1,
方
42
的
1
2
4
ξ
1
于
42
从
41
列
1
一
14,
产生
,1 4
就能
41
们
1
我
,
,
1 4
此
2 1.999396 = 0.000604 , 2 1.99996164 = 0.00003836,
用同样的方法,我们可以制定取ξ2的过剩近似值y的方式:
小数
个!
经由对不足近似值的计算过程 ,我们可以得到一列从大于ξ2的方向逐渐逼近ξ2的数:
1.5 > 1.42 > 1.415 > 1.4143 > 1.41422 > 1.414214 > > ξ2. 这串数字y就是ξ2的过剩近似值.
的那
为三
于ξ2
个值
大
三
且
第
在同位数的小数中最接近ξ
之后第二个值为两位小数
是
5,
总
1.
且,y
个值为
小数,
y的第
位
,
加
于
增
大
次
都
即每
列数y
高中数学
小数位数相同的v2的过剩近似值y与不足近似值x 的差是有规律的:
高中数学
1. 1,
这个差值就是我们常说的ξ2的近似值得精确度 , 如果我们需要一个精确到
0.001 的ξ2的近似值 , 就可以用 1.414.
当ξ2的不足近似值x和过剩近似值y逐渐逼近ξ2时,我们也就得到了精度越来越
高的ξ2的近似值 ,这样一直计算下去 ,我们就可以得到任何精确度的ξ2的近似值.
高中数学
4
1
1.4143 1.4 42 = 0.0001,
高中数学
这个用有理数指数幂逼近无理数指数幂的方法是可以推广的 ,比如2ξ3 , 3π
的值 , 都可以用此方法近似的等于一个有理数指数幂的值.
实数指数幂的运算性质:
对于任意的正数a, b , 都有:
① aT aS = aT +S ,
② aT S = aTS , T, S ∈ R.
③ ab T = aT bT ,
高中数学
例 2. 按从小到大的顺序,可将2ξ3 ,3ξ2 ,π ξ5,2π 重新排列为 (可用
计算工具) .
解: 四个数均为无理数指数幂 ,我们不妨取ξ2, ξ3, ξ5, π 的近似值 ,计算无理数指数幂的近
似值. 不妨精确到 0.001.
ξ2 = 1.414, ξ3 = 1.732, ξ5 = 2.236, π = 3. 142.
2ξ3 = 3.322, 3ξ2 = 4.728, π ξ5 = 12.935, 2π = 8.827.
所以 , 重新排列为2ξ3 , 3ξ2 , 2π , 3ξ5 .
高中数学
总结:
(1)理解由有理数指数幂逼近无理数指数幂的原理;
高中数学
总结:
(2) 实数指数幂的运算性质:
对于任意的a > 0 , b > 0 , T, S ∈ R ,都有:
① aT aS = aT +S ,
② aT S = aTS ,
③ ab T = aT bT ,
高中数学
总结:
(3)用指数幂的形式来表示根式,往往会简化根式运算. 运算时尽量化为同
底数的幂,即便各项不能都化为相同的底数,也要尽可能地减少底数的种类.
高中数学
因为喜欢而学习, 因为通透而热爱!
让我们 一起加油!
高中数学
(l 整数
有理数{l(分数{无 数
实数{无理数: 环小数,例如V2 , V3 , π .
高中数学
无限不循
有理数
限循环小
有限小数
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
