物理人教版(2019)选择性必修第二册1.3带电粒子在匀强磁场中的运动(共43张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第二册1.3带电粒子在匀强磁场中的运动(共43张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-11-30 08:03:19 | ||
图片预览






文档简介
(共43张PPT)
1.3 带电粒子在匀强磁场中的运动
常见粒子的分类
带电的基本粒子:
如电子,质子,α粒子,正负离子等。这些粒子所受重力和洛仑磁力相比在小得多,除非有说明或明确的暗示以外,一般都不考虑重力。(但并不能忽略质量)。
2. 带电微粒:
如带电小球、液滴、尘埃等。除非有说明或明确的暗示以外,一般都考虑重力。
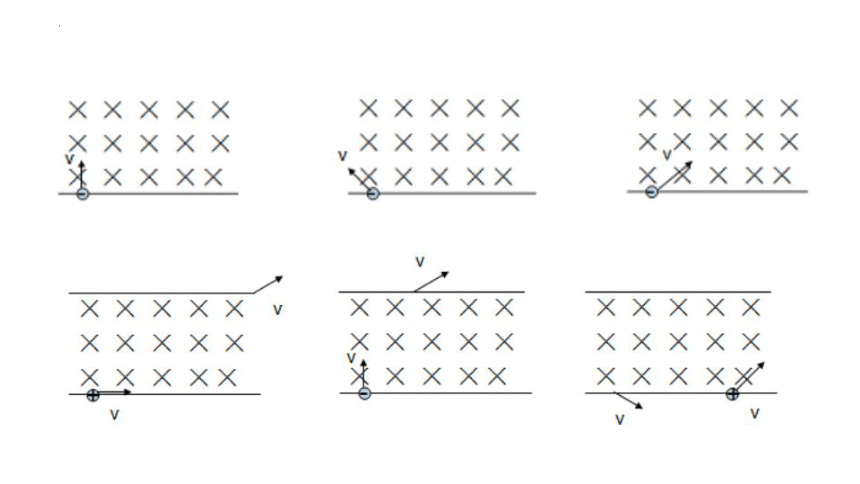
情形1. 带电粒子平行射入匀强磁场的运动状态? (重力不计)
V ∥B F洛 = 0 粒子做匀速直线运动
情形2. 带电粒子垂直磁场射入匀强磁场, 做匀速圆周运动
由牛顿第二定律得
1.轨道半径:
2.周期:
3.a到b 的时间:
为圆心角
为速度偏转角
为弦切角
1. (多选)带电粒子飞入匀强磁场后,下列说法正确的是 ( )
A.一定做匀速圆周运动
B.做匀速圆周运动时,速度一定不变
C.做匀速圆周运动时,洛伦兹力的方向总和运动方向垂直
D.做匀速圆周运动时,动能一定保持不变
【答案】CD
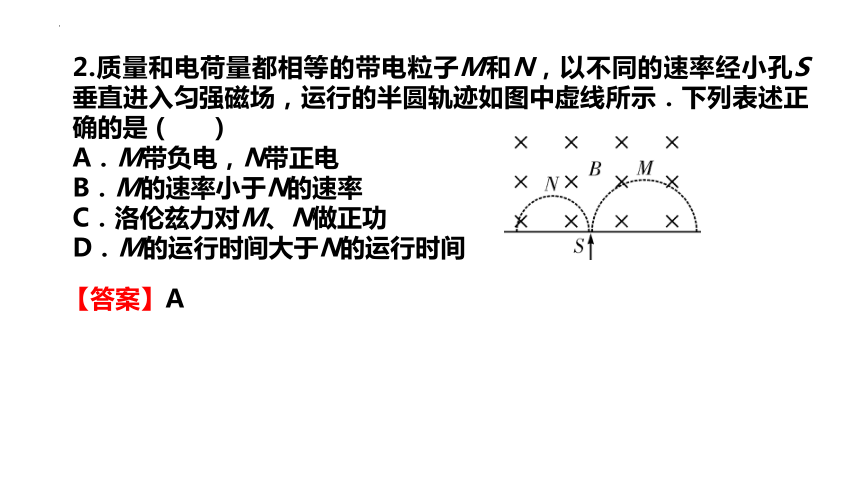
2.质量和电荷量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示.下列表述正确的是 ( )
A.M带负电,N带正电
B.M的速率小于N的速率
C.洛伦兹力对M、N做正功
D.M的运行时间大于N的运行时间
【答案】A
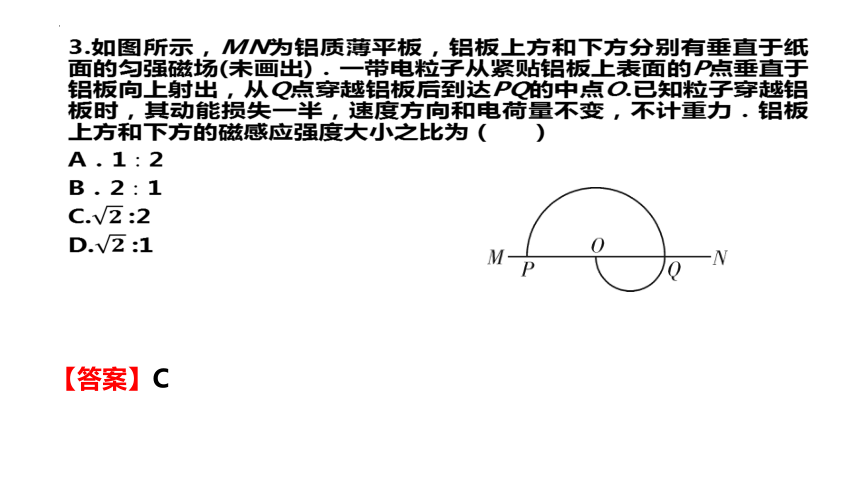
3.如图所示,MN为铝质薄平板,铝板上方和下方分别有垂直于纸面的匀强磁场(未画出).一带电粒子从紧贴铝板上表面的P点垂直于铝板向上射出,从Q点穿越铝板后到达PQ的中点O.已知粒子穿越铝板时,其动能损失一半,速度方向和电荷量不变,不计重力.铝板上方和下方的磁感应强度大小之比为 ( )
A.1∶2
B.2∶1
C.:2
D.:1
【答案】C
一、解题思路:
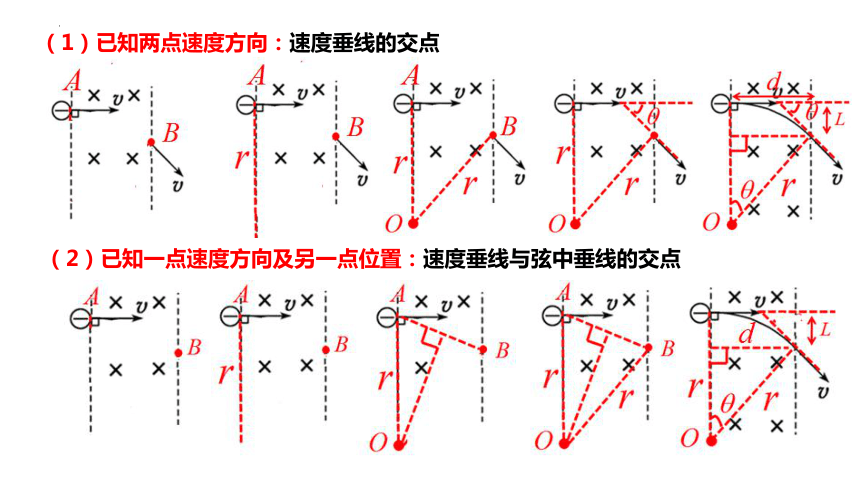
1.找圆心:
(1)已知两点速度方向:速度垂线的交点
(2)已知一点速度方向及另一点位置:速度垂线与弦中垂线的交点
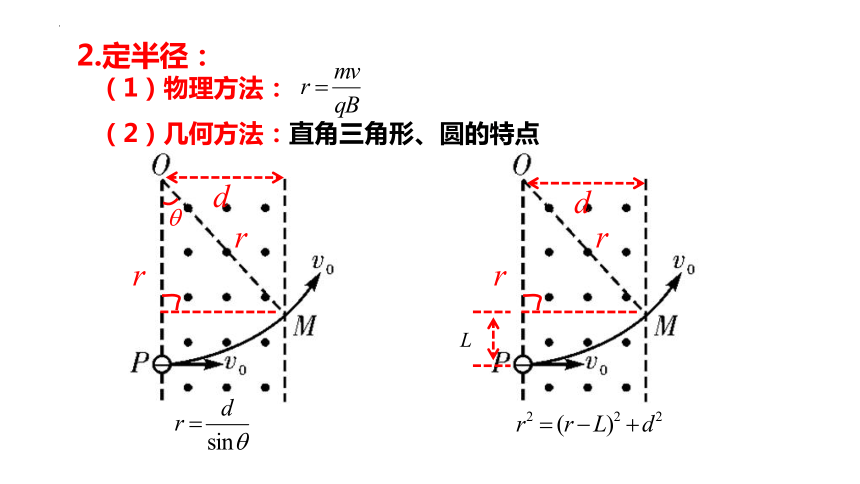
2.定半径:
(1)物理方法:
(2)几何方法:直角三角形、圆的特点
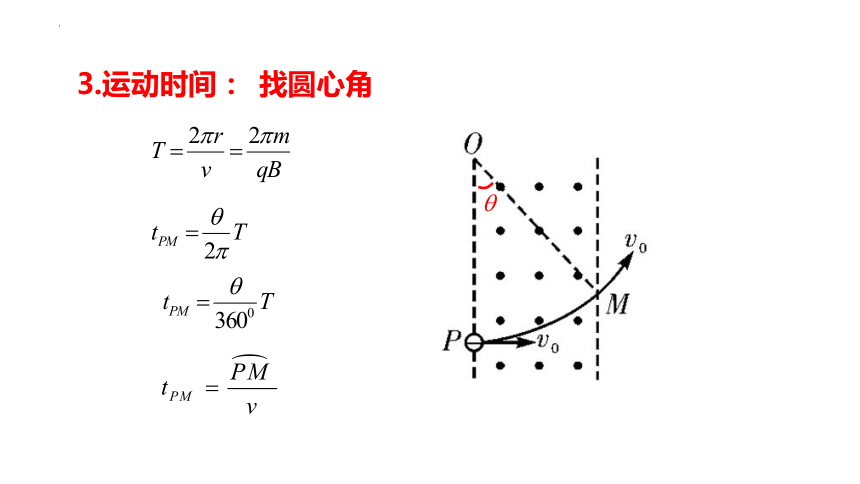
3.运动时间:
找圆心角
(1)已知两点速度方向:速度垂线的交点
(2)已知一点速度方向及另一点位置:速度垂线与弦中垂线的交点
4.如图,一个边长为a的正方形区域内存在垂直于纸面向里的匀强磁场,磁感应强度大小为B.现有一质量为m、带电量为-q的粒子以某一速度从AB的中点平行于BC边射入磁场,粒子恰好从C点射出,不计粒子重力.则粒子入射磁场的速度大小为 ( )
【答案】B
5.如图所示,一束电子流以速度v通过一处于矩形空间的匀强磁场,速度方向与磁感线垂直,且平行于矩形空间的其中一边,矩形空间边长为a和a,电子刚好从矩形的相对的AC两个顶点间通过,求:(1)电子在磁场中做圆周运动的半径;(2)电子在磁场中的飞行时间。
6.如图所示,一个质量为m、电荷量为-q、不计重力的带电粒子从x轴上的P(a,0)点以速度v,沿与x轴正方向成600的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限,求:
(1)匀强磁场的磁感应强度B;
(2)穿过第一象限的时间.
二、轨迹特点:
1.直线边界:(1)对称; (2)怎样进怎样出;
1.直线边界:(1)对称; (2)怎样进怎样出;
二、轨迹特点:
1.直线边界:(1)对称; (2)怎样进怎样出;
7.在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸里,磁感应强度为B.一带负电的粒子(质量为m、电荷量为q)以速度v从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.求:
(1)该粒子射出磁场的位置;
(2)该粒子在磁场中运动的时间.
θ
θ
解:(1)设从A点射出磁场,O、A间的距离为L,由牛顿第二定律得
解得
θ
θ
由几何关系得
解得
粒子离开磁场的位置坐标为
(2)粒子做匀速圆周运动的周期
粒子在磁场中运动的时间
8.如图所示,两匀强磁场的方向相同,以虚线MN为理想边界,磁感应强度大小分别为B1、B2,一质量为m、电荷量为e的电子从MN上的P点沿垂直于磁场方向射入匀强磁场B1中,其运动轨迹为如图虚线所示的“心”形图线.则以下说法正确的是 ( )
【答案】B
9.如图所示,在第一象限内有垂直纸面向里的匀强磁场(磁场足够大),一对正、负电子(质量、电量相等,但电性相反)分别以相同速度沿与x轴成30°角的方向从原点垂直磁场射入,则负电子与正电子在磁场中运动时间之比为(不计正、负电子间的相互作用力)( )
A.1∶ B.2∶1 C.∶1 D.1∶2
【答案】D
2.圆形边界:径向入径向出
二、轨迹特点:
10.(2021年全国乙卷)如图,圆形区域内有垂直纸面向里的匀强磁场,质量为m、电荷量为q(q>0)的带电粒子从圆周上的M点沿直径MON方向射入磁场.若粒子射入磁场时的速度大小为v1 ,离开磁场时速度方向偏转90°;若射入磁场时的速度大小为v2 ,离开磁场时速度方向偏转60°,不计重力,则 为
【答案】B
11.如图所示,虚线圆所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B。一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动方向与原入射方向成θ角。设电子质量为m,电荷量为e,不计电子之间相互作用力及所受的重力,求:
(1)电子在磁场中运动轨迹的半径R;
(2)电子在磁场中运动的时间t;
(3)圆形磁场区域的半径r。
解:(1)由牛顿第二定律得
解得
(2)电子做匀速圆周运动的周期
电子在磁场中运动的时间
(3)由如图所示几何关系得
解得
3.平行边界:有临界,轨迹与磁场边界相切,常用伸缩圆。
3.平行边界:有临界,轨迹与磁场边界相切,常用伸缩圆。
12.如图所示,一束电荷量为e的电子以垂直于磁感应强度B并垂直于磁场边界的速度v射入宽度为d的匀强磁场中,穿出磁场时速度方向和原来射入方向的夹角为θ=600.求:
(1)电子的质量;(2)穿越磁场的时间.
13.两个等质量粒子分别以速度va和vb垂直射入有界匀强磁场,两粒子的入射方向与磁场边界的夹角分别为60°和45°,磁场垂直纸面向外,磁场宽度为d,两粒子同时由A点出发,同时到达B点,A、B连线垂直于磁场边界.如图所示,则( )
A.a 粒子带负电,b粒子带正电
B.两粒子的轨道半径之比Ra∶Rb=1∶
C.两粒子的电荷量之比qa∶qb=3∶2
D.两粒子的速率之比va∶vb=2∶3
【答案】D
14.如图所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v从O 点垂直射入.已知两板之间距离为d.板长为d, O点是NP板的正中点,为使粒子能从两板之间射出,试求磁感应强度B应满足的条件(已知质子带电荷量为q,质量为m).
解:如果质子恰好从N点射出,则有
解得
由牛顿第二定律得
如果质子恰好从M点射出,则有
解得
由牛顿第二定律得
所以B应满足
15.一磁场宽度为L,磁感应强度为B,如图所示,一电荷质量为m、带电荷量为-q,不计重力,以某一速度(方向如图)射入磁场.若不使其从右边界飞出,则电荷的速度应为多大?
先确定圆心在虚线上,分别画出半径逐渐增大的轨迹图
图1
图2
图3
图4
图5
①图1至图3 ,v增大,r增大,图1至图3均从左边界飞出,但图3速度恰好与右边界相切,是临界状态。
②v继续增大,r增大,如图5,粒子从右边界飞出。
关键:找出临界状态:速度方向与右边界相切
15.一磁场宽度为L,磁感应强度为B,如图所示,一电荷质量为m、带电荷量为-q,不计重力,以某一速度(方向如图)射入磁场.若不使其从右边界飞出,则电荷的速度应为多大?
解:当速度方向与右边界相切时,粒子恰好不从右边界飞出,轨迹如图
由几何关系得
由牛顿第二定律得
解得
所以
16.如图,边界MN下方是一垂直纸面向里的匀强磁场,甲、乙两带电粒子先后从c点沿与MN成45°角的方向射入磁场,最后都从d点射出磁场.已知,m甲=4m乙,q甲=2q乙,不计粒子的重力.则( )
A.两粒子的速率相同
B.两粒子的动能相同
C.两粒子在磁场内运动的时间相同
D.两粒子可能带异种电荷
【答案】B
1.找圆心:
①已知两点速度方向:速度垂线的交点
②已知一点速度方向及另一点位置:速度垂线与弦中垂线的交点
2.定半径:
①
②
A错
由图可知,轨道半径相同,圆心角相同
B对
C错
D错:由图可知,轨迹相同,故同种电荷
17,如图所示,圆形区域内有垂直纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a,b,c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力的作用,则下列说法正确的是
B对:
A.a粒子速率最大,在磁场中运动时间最长
B.c粒子速率最大,在磁场中运动时间最短
C.a粒子速率最小,在磁场中运动时间最短
D.c粒子速率最小,在磁场中运动时间最短
带电粒子从圆形磁场沿半径方向射入,则必定沿半径方向射出。(得记得)
由上述各式得:
由图可知:
18.如图所示,半径为R的圆形区域内有垂直于纸面向里的匀强磁场.重力不计、电荷量一定的带电粒子以速度v正对着圆心O射入磁场,若粒子射入、射出磁场点间的距离为R,则粒子在磁场中的运动时间为
( )
【答案】A
19.如图所示,在匀强电场和匀强磁场共存的区域内,电场的场强为E,方向竖直向下,磁场的磁感应强度为B,方向垂直纸面向里,一质量为m的带电粒子,在场区内的一竖直平面做匀速圆周运动,则可判断该带电粒子( )
A.带有电量为 的正电荷
B.沿圆周逆时针运动
C.运动的角速度为
D.运动的速率为
B错:粒子带负电,由左手定则可知:顺时针运动
A错:
C对:
D错:
解:1.由“粒子做匀速圆周运动”得:合力指向圆心
2.受力分析:洛伦兹力指向圆心,重力竖直向下,电场力在竖直方向,故
1.3 带电粒子在匀强磁场中的运动
常见粒子的分类
带电的基本粒子:
如电子,质子,α粒子,正负离子等。这些粒子所受重力和洛仑磁力相比在小得多,除非有说明或明确的暗示以外,一般都不考虑重力。(但并不能忽略质量)。
2. 带电微粒:
如带电小球、液滴、尘埃等。除非有说明或明确的暗示以外,一般都考虑重力。
情形1. 带电粒子平行射入匀强磁场的运动状态? (重力不计)
V ∥B F洛 = 0 粒子做匀速直线运动
情形2. 带电粒子垂直磁场射入匀强磁场, 做匀速圆周运动
由牛顿第二定律得
1.轨道半径:
2.周期:
3.a到b 的时间:
为圆心角
为速度偏转角
为弦切角
1. (多选)带电粒子飞入匀强磁场后,下列说法正确的是 ( )
A.一定做匀速圆周运动
B.做匀速圆周运动时,速度一定不变
C.做匀速圆周运动时,洛伦兹力的方向总和运动方向垂直
D.做匀速圆周运动时,动能一定保持不变
【答案】CD
2.质量和电荷量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示.下列表述正确的是 ( )
A.M带负电,N带正电
B.M的速率小于N的速率
C.洛伦兹力对M、N做正功
D.M的运行时间大于N的运行时间
【答案】A
3.如图所示,MN为铝质薄平板,铝板上方和下方分别有垂直于纸面的匀强磁场(未画出).一带电粒子从紧贴铝板上表面的P点垂直于铝板向上射出,从Q点穿越铝板后到达PQ的中点O.已知粒子穿越铝板时,其动能损失一半,速度方向和电荷量不变,不计重力.铝板上方和下方的磁感应强度大小之比为 ( )
A.1∶2
B.2∶1
C.:2
D.:1
【答案】C
一、解题思路:
1.找圆心:
(1)已知两点速度方向:速度垂线的交点
(2)已知一点速度方向及另一点位置:速度垂线与弦中垂线的交点
2.定半径:
(1)物理方法:
(2)几何方法:直角三角形、圆的特点
3.运动时间:
找圆心角
(1)已知两点速度方向:速度垂线的交点
(2)已知一点速度方向及另一点位置:速度垂线与弦中垂线的交点
4.如图,一个边长为a的正方形区域内存在垂直于纸面向里的匀强磁场,磁感应强度大小为B.现有一质量为m、带电量为-q的粒子以某一速度从AB的中点平行于BC边射入磁场,粒子恰好从C点射出,不计粒子重力.则粒子入射磁场的速度大小为 ( )
【答案】B
5.如图所示,一束电子流以速度v通过一处于矩形空间的匀强磁场,速度方向与磁感线垂直,且平行于矩形空间的其中一边,矩形空间边长为a和a,电子刚好从矩形的相对的AC两个顶点间通过,求:(1)电子在磁场中做圆周运动的半径;(2)电子在磁场中的飞行时间。
6.如图所示,一个质量为m、电荷量为-q、不计重力的带电粒子从x轴上的P(a,0)点以速度v,沿与x轴正方向成600的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限,求:
(1)匀强磁场的磁感应强度B;
(2)穿过第一象限的时间.
二、轨迹特点:
1.直线边界:(1)对称; (2)怎样进怎样出;
1.直线边界:(1)对称; (2)怎样进怎样出;
二、轨迹特点:
1.直线边界:(1)对称; (2)怎样进怎样出;
7.在y<0的区域内存在匀强磁场,磁场方向垂直于xy平面并指向纸里,磁感应强度为B.一带负电的粒子(质量为m、电荷量为q)以速度v从O点射入磁场,入射方向在xy平面内,与x轴正向的夹角为θ.求:
(1)该粒子射出磁场的位置;
(2)该粒子在磁场中运动的时间.
θ
θ
解:(1)设从A点射出磁场,O、A间的距离为L,由牛顿第二定律得
解得
θ
θ
由几何关系得
解得
粒子离开磁场的位置坐标为
(2)粒子做匀速圆周运动的周期
粒子在磁场中运动的时间
8.如图所示,两匀强磁场的方向相同,以虚线MN为理想边界,磁感应强度大小分别为B1、B2,一质量为m、电荷量为e的电子从MN上的P点沿垂直于磁场方向射入匀强磁场B1中,其运动轨迹为如图虚线所示的“心”形图线.则以下说法正确的是 ( )
【答案】B
9.如图所示,在第一象限内有垂直纸面向里的匀强磁场(磁场足够大),一对正、负电子(质量、电量相等,但电性相反)分别以相同速度沿与x轴成30°角的方向从原点垂直磁场射入,则负电子与正电子在磁场中运动时间之比为(不计正、负电子间的相互作用力)( )
A.1∶ B.2∶1 C.∶1 D.1∶2
【答案】D
2.圆形边界:径向入径向出
二、轨迹特点:
10.(2021年全国乙卷)如图,圆形区域内有垂直纸面向里的匀强磁场,质量为m、电荷量为q(q>0)的带电粒子从圆周上的M点沿直径MON方向射入磁场.若粒子射入磁场时的速度大小为v1 ,离开磁场时速度方向偏转90°;若射入磁场时的速度大小为v2 ,离开磁场时速度方向偏转60°,不计重力,则 为
【答案】B
11.如图所示,虚线圆所围区域内有方向垂直纸面向里的匀强磁场,磁感应强度为B。一束电子沿圆形区域的直径方向以速度v射入磁场,电子束经过磁场区后,其运动方向与原入射方向成θ角。设电子质量为m,电荷量为e,不计电子之间相互作用力及所受的重力,求:
(1)电子在磁场中运动轨迹的半径R;
(2)电子在磁场中运动的时间t;
(3)圆形磁场区域的半径r。
解:(1)由牛顿第二定律得
解得
(2)电子做匀速圆周运动的周期
电子在磁场中运动的时间
(3)由如图所示几何关系得
解得
3.平行边界:有临界,轨迹与磁场边界相切,常用伸缩圆。
3.平行边界:有临界,轨迹与磁场边界相切,常用伸缩圆。
12.如图所示,一束电荷量为e的电子以垂直于磁感应强度B并垂直于磁场边界的速度v射入宽度为d的匀强磁场中,穿出磁场时速度方向和原来射入方向的夹角为θ=600.求:
(1)电子的质量;(2)穿越磁场的时间.
13.两个等质量粒子分别以速度va和vb垂直射入有界匀强磁场,两粒子的入射方向与磁场边界的夹角分别为60°和45°,磁场垂直纸面向外,磁场宽度为d,两粒子同时由A点出发,同时到达B点,A、B连线垂直于磁场边界.如图所示,则( )
A.a 粒子带负电,b粒子带正电
B.两粒子的轨道半径之比Ra∶Rb=1∶
C.两粒子的电荷量之比qa∶qb=3∶2
D.两粒子的速率之比va∶vb=2∶3
【答案】D
14.如图所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v从O 点垂直射入.已知两板之间距离为d.板长为d, O点是NP板的正中点,为使粒子能从两板之间射出,试求磁感应强度B应满足的条件(已知质子带电荷量为q,质量为m).
解:如果质子恰好从N点射出,则有
解得
由牛顿第二定律得
如果质子恰好从M点射出,则有
解得
由牛顿第二定律得
所以B应满足
15.一磁场宽度为L,磁感应强度为B,如图所示,一电荷质量为m、带电荷量为-q,不计重力,以某一速度(方向如图)射入磁场.若不使其从右边界飞出,则电荷的速度应为多大?
先确定圆心在虚线上,分别画出半径逐渐增大的轨迹图
图1
图2
图3
图4
图5
①图1至图3 ,v增大,r增大,图1至图3均从左边界飞出,但图3速度恰好与右边界相切,是临界状态。
②v继续增大,r增大,如图5,粒子从右边界飞出。
关键:找出临界状态:速度方向与右边界相切
15.一磁场宽度为L,磁感应强度为B,如图所示,一电荷质量为m、带电荷量为-q,不计重力,以某一速度(方向如图)射入磁场.若不使其从右边界飞出,则电荷的速度应为多大?
解:当速度方向与右边界相切时,粒子恰好不从右边界飞出,轨迹如图
由几何关系得
由牛顿第二定律得
解得
所以
16.如图,边界MN下方是一垂直纸面向里的匀强磁场,甲、乙两带电粒子先后从c点沿与MN成45°角的方向射入磁场,最后都从d点射出磁场.已知,m甲=4m乙,q甲=2q乙,不计粒子的重力.则( )
A.两粒子的速率相同
B.两粒子的动能相同
C.两粒子在磁场内运动的时间相同
D.两粒子可能带异种电荷
【答案】B
1.找圆心:
①已知两点速度方向:速度垂线的交点
②已知一点速度方向及另一点位置:速度垂线与弦中垂线的交点
2.定半径:
①
②
A错
由图可知,轨道半径相同,圆心角相同
B对
C错
D错:由图可知,轨迹相同,故同种电荷
17,如图所示,圆形区域内有垂直纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a,b,c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力的作用,则下列说法正确的是
B对:
A.a粒子速率最大,在磁场中运动时间最长
B.c粒子速率最大,在磁场中运动时间最短
C.a粒子速率最小,在磁场中运动时间最短
D.c粒子速率最小,在磁场中运动时间最短
带电粒子从圆形磁场沿半径方向射入,则必定沿半径方向射出。(得记得)
由上述各式得:
由图可知:
18.如图所示,半径为R的圆形区域内有垂直于纸面向里的匀强磁场.重力不计、电荷量一定的带电粒子以速度v正对着圆心O射入磁场,若粒子射入、射出磁场点间的距离为R,则粒子在磁场中的运动时间为
( )
【答案】A
19.如图所示,在匀强电场和匀强磁场共存的区域内,电场的场强为E,方向竖直向下,磁场的磁感应强度为B,方向垂直纸面向里,一质量为m的带电粒子,在场区内的一竖直平面做匀速圆周运动,则可判断该带电粒子( )
A.带有电量为 的正电荷
B.沿圆周逆时针运动
C.运动的角速度为
D.运动的速率为
B错:粒子带负电,由左手定则可知:顺时针运动
A错:
C对:
D错:
解:1.由“粒子做匀速圆周运动”得:合力指向圆心
2.受力分析:洛伦兹力指向圆心,重力竖直向下,电场力在竖直方向,故
