新人教B版必修第三册高中数学第七章 三角函数 素养测评(含解析)
文档属性
| 名称 | 新人教B版必修第三册高中数学第七章 三角函数 素养测评(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 98.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 07:39:13 | ||
图片预览



文档简介
第七章 素养测评
时间:120分钟 满分:150分
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知点P(,-)是角α的终边与单位圆的交点,则cos α=( )
A.- B. C.- D.-
2.已知sin α=-,且α是第三象限角,则tan α的值为( )
A. B.- C. D.-
3.已知扇形的半径为r,周长为3r,则扇形的圆心角等于( )
A. B.1 C. D.3
4.已知θ是第二象限角,则 可化简为( )
A.sin θcos θ B.-sin θcos θ C.2sin θcos θ D.-2sin θcos θ
5.tan =( )
A. B.- C. D.-
6.若p:tan (α+2 021π)<0且cos (α-)>0,q:α为第二象限角.则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.已知-<α<0,sin α+cos α=,则的值为( )
A. B. C. D.-
8.将函数f(x)=sin(2x+)的图象分别向左、向右平移φ(φ>0)个单位长度后,所得的图象都关于y轴对称,则φ的最小值分别为( )
A., B., C., D.,
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有错选的得0分.
9.下列命题正确的是( )
A.在与530°角终边相同的角中,最小的正角为170°
B.若角α的终边过点P(-4,3),则cos α=-
C.已知θ是第二象限角,则tan (sin θ)>tan (cos θ)
D.若一扇形弧长为2,圆心角为90°,则该扇形的面积为
10.已知函数f(x)=tan x,则下列结论正确的是( )
A.2π是f(x)的一个周期 B.f(-)=f()
C.f(x)的值域为RD.f(x)的图象关于点(,0)对称
11.已知函数f(x)=-cos (4x-),则下列说法错误的是( )
A.f(x)的最小正周期为π
B.f(x)的图象关于直线x=对称
C.f(x)的单调递增区间为[-,+](k∈Z)
D.f(x)的图象关于点(,0)对称
12.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,已知时间t=0时,点A的坐标是(,),则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间可以是( )
A.[0,1] B.[1,7] C.[7,12] D.[1,12]
三、填空题:本题共4小题,每小题5分,共20分.
13.写出一个定义域为R,周期为π的偶函数f(x)=________.
14.已知f(x)=sin x+tan x+x-1,若f(a)=3,则f(-a)=________.
15.把函数y=sin (5x-)的图象向右平移个单位,再把所得函数图象上各点的横坐标缩短为原来的,所得的函数图象对应的解析式为______________________.
16.已知函数f(x)=2sin (ωx-)+1(x∈R)图象的一条对称轴方程为x=π,其中ω为常数,且ω∈(1,2),则函数f(x)的最小正周期为________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知tan α=3,求下列各式的值:
(1);
(2)2sin2α-3sinαcos α-1.
18.(12分)已知θ是第二象限角,5sin θcos θ=4tan (π+θ),求:
(1)tan θ;
(2).
19.(12分)已知函数f(x)=sin (2x-).
(1)用五点法,画出函数f(x)在一个周期上的图象;
(2)当x∈[-,]时,f(x)-a=0有解,求实数a的取值范围.
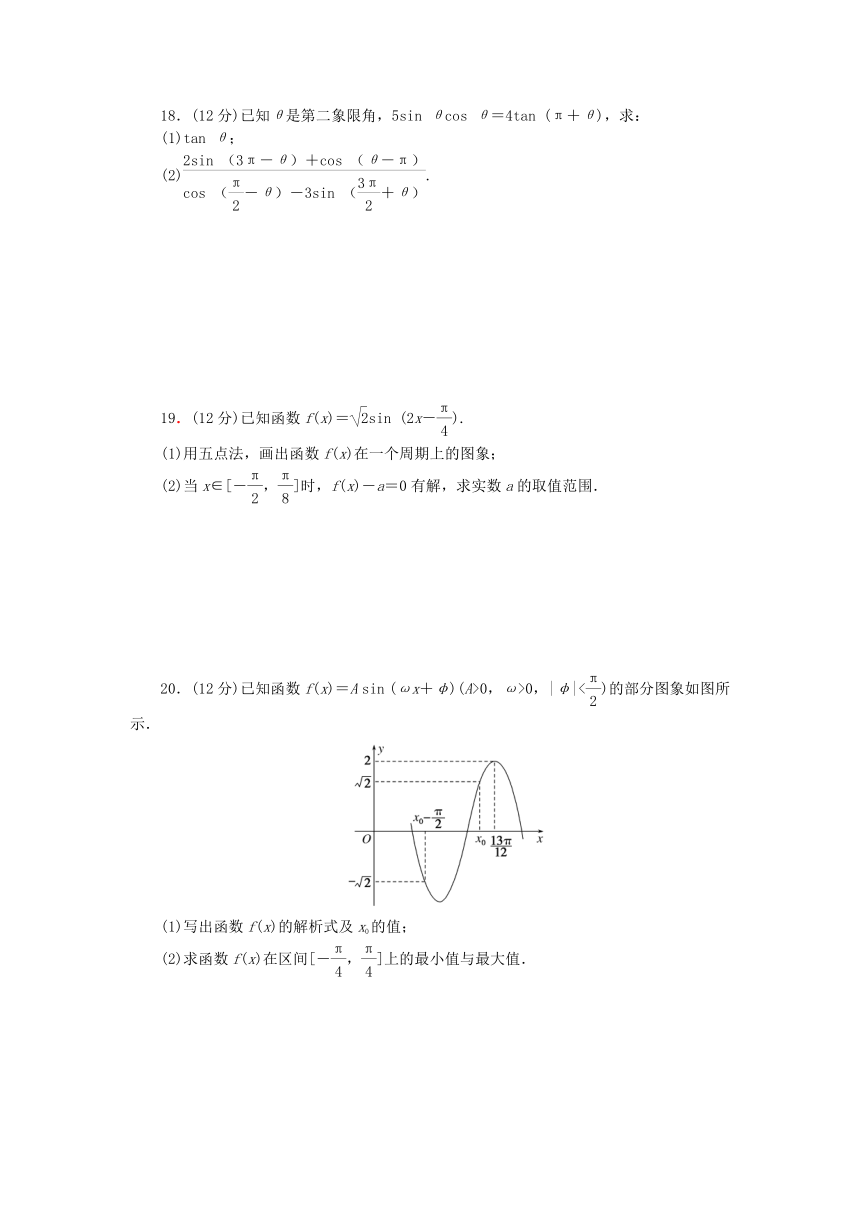
20.(12分)已知函数f(x)=A sin (ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.
(1)写出函数f(x)的解析式及x0的值;
(2)求函数f(x)在区间[-,]上的最小值与最大值.
21.(12分)已知函数f(x)=sin (2x+φ),φ∈(0,π),且f(x)的图象关于x=对称.
(1)求f(x)的解析式;
(2)将f(x)图象上的所有点向左平移m(m>0)个单位,得到y=g(x)的图象,若y=g(x)的图象关于点(,0)对称,求当m取最小值时,函数y=g(x)的单调递增区间.
22.(12分)若函数f(x)=A sin (ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.
(1)求函数y=f(x)的解析式;
(2)当x∈[-,]时,不等式|f(x)-m|≤1有解,求实数m的取值范围.
第七章 素养测评
1.答案:B
解析:因为点P(,-)是角α的终边与单位圆的交点,所以cosα=,
故选B.
2.答案:A
解析:由sinα=-,且α是第三象限角,易得cosα=-,故tanα=.
3.答案:B
解析:弧长l=3r-2r=r,则圆心角α==1.
4.答案:B
解析:===|sinθcosθ|,由于θ为第二象限角,所以|sinθcosθ|=-sinθcosθ,故选B.
5.答案:B
解析:tan=tan (2π-)=tan (-)=-tan=-.故选B.
6.答案:C
解析:由题意得tan (α+2021π)=tanα<0,cos (α-)=sinα>0,由p能推出q,由q能推出p,故p是q的充要条件.故选C.
7.答案:B
解析:因为-<α<0,所以sinα<0,cosα>0,
又?sinα+cosα=
sin2α+cos2α=1?,即2cos2α-cosα-=0,解得cosα=,sinα=-,所以==,故选B.
8.答案:A
解析:函数f(x)的图象向左平移φ个单位长度得到函数g(x)=sin(2x+2φ+)的图象,向右平移φ个单位长度得函数h(x)=sin (2x-2φ+)的图象,于是,2φ+=+kπ,k∈Z,-2φ+=+kπ,k∈Z,于是φ的最小值分别为,.故选A.
9.答案:ABC
解析:选项A:由0°故所求的最小正角β=170°.正确;
选项B:由三角函数的定义可得cosα==-.正确;
选项C:∵θ是第二象限角,∴00,tan (cosθ)<0,∴tan (sinθ)>tan (cosθ).正确;
选项D:弧长为2,圆心角为90°,则扇形的半径为,所以扇形面积为×2×=.错误.故选ABC.
10.答案:ACD
解析:f(x)=tanx的最小正周期为π,所以2π是f(x)的一个周期,A项正确;f(-)=1,f()=-1,B项错误;f(x)=tanx的值域为R,C项正确;f(x)=tanx的图象关于点(,0)对称,D项正确.故选ACD.
11.答案:ABC
解析:对于函数f(x)=-cos (4x-),它的最小正周期为=,故A错误;当x=时,f(x)=0,故f(x)的图象关于点(,0)对称,故D正确,而B错误;令2kπ≤4x-≤2kπ+π,k∈Z,得+≤x≤+,k∈Z,故函数的增区间为[+,+],k∈Z,故C错误.故选ABC.
12.答案:AC
解析:由题意知T=12,∴ω==,从而设y关于t的函数为y=sin (t+φ).又∵t=0时,y=,∴可取φ=,∴y=sin (t+),∴当2kπ-≤t+≤2kπ+(k∈Z),即12k-5≤t≤12k+1(k∈Z)时,函数递增.∵0≤t≤12,∴函数的单调递增区间为[0,1]和[7,12].
13.答案:cos2x(答案不唯一)
解析:y=cos2x满足定义域为R,最小正周期T==π,且为偶函数,符合要求.
14.答案:-5
解析:由于f(a)=3,即sina+tana+a-1=3,故sina+tana+a=4,令g(x)=sinx+tanx+x,则g(-x)=-sinx-tanx-x=-g(x),即g(x)在定义域内是奇函数,满足sina+tana+a=-(sin (-a)+tan (-a)+(-a),则sin (-a)+tan (-a)+(-a)=-4,故f(-a)=sin (-a)+tan (-a)+(-a)-1=-4-1=-5.
15.答案:y=sin (10x-)
解析:将函数y=sin (5x-)的图象向右平移个单位,得到函数y=sin [5(x-)-]=sin (5x-)的图象,再把所得图象上各点的横坐标缩短为原来的,可得到函数y=sin (10x-)的图象.
16.答案:
解析:由f(x)=2sin (ωx-)+1(x∈R)图象的一条对称轴为直线x=π,可得ωπ-=kπ+(k∈Z),∴ω=k+(k∈Z).又∵ω∈(1,2),∴ω=,∴f(x)的最小正周期为T==.
17.解析:(1)原式====.
(2)原式=
===-.
18.解析:(1)由题意,角θ是第二象限角,且5sinθcosθ=4tan (π+θ),
可得5sinθcosθ=4tanθ=,可得cos2θ=,所以sin2θ=1-cos2θ=,
所以tan2θ==,
因为θ是第二象限角,可得tanθ=-.
(2)由(1)知tanθ=-,
又由====-.
19.解析:(1)列表如下:
x
2x- 0 π 2π
f(x) 0 0 - 0
描点、连线,如图所示.
(2)∵-≤x≤,
∴-≤2x-≤0,
∴-1≤sin (2x-)≤,
∴-≤sin (2x-)≤1.
∵f(x)-a=0有解,即a=f(x)有解,∴a∈[-,1].
20.解析:(1)∵A>0,ω>0,
∴由函数图象可知A=2,T==2[x0-(x0-)]=π,解得ω=2.
又∵函数图象过点(,2),∴2=2sin (2×+φ),
∴2×+φ=2kπ+(k∈Z),即φ=2kπ-,k∈Z.
又∵|φ|<,∴φ=,∴f(x)=2sin (2x+).
由函数图象可得2sin (2x0+)=,
∴2x0+=2kπ+,k∈Z,即x0=kπ-,k∈Z.
又∵-(2)由x∈[-,],可得2x+∈[-,].当2x+=-,即x=-时,f(x)min=f(-)=-1;
当2x+=,即x=时,f(x)max=f()=2.
21.解析:(1)依题意有2×+φ=+kπ,k∈Z,
∴φ=+kπ,k∈Z,
又φ∈(0,π),∴φ=,
∴f(x)=sin (2x+).
(2)将f(x)图象上所有的点向左平移m(m>0)个单位,
得到y=g(x)=sin (2x++2m).
∵y=g(x)的图象关于点(,0)对称,
∴sin (2×++2m)=0,
∴+2m=kπ,k∈Z,
∴m=-,k∈Z.
∵m>0,∴当k=1时,m有最小值,
∴g(x)=sin (2x+).
由-+2kπ≤2x+≤+2kπ,k∈Z,
得[-+kπ,-+kπ],k∈Z.
∴函数的单调递增区间是[-+kπ,-+kπ],k∈Z.
22.解析:(1)由题图,知A=2,T=-(-)=,解得T=π,所以ω==2.根据“五点法”作图,可得2×+φ=2kπ+,k∈Z,解得φ=2kπ+,k∈Z.又因为|φ|<,所以φ=.所以f(x)=2sin (2x+).
(2)当x∈[-,]时,2x+∈[,],所以f(x)∈[1,2].
因为|f(x)-m|≤1有解,所以m-1≤f(x)≤1+m有解,即即
解得0≤m≤3.故实数m的取值范围是[0,3].
时间:120分钟 满分:150分
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知点P(,-)是角α的终边与单位圆的交点,则cos α=( )
A.- B. C.- D.-
2.已知sin α=-,且α是第三象限角,则tan α的值为( )
A. B.- C. D.-
3.已知扇形的半径为r,周长为3r,则扇形的圆心角等于( )
A. B.1 C. D.3
4.已知θ是第二象限角,则 可化简为( )
A.sin θcos θ B.-sin θcos θ C.2sin θcos θ D.-2sin θcos θ
5.tan =( )
A. B.- C. D.-
6.若p:tan (α+2 021π)<0且cos (α-)>0,q:α为第二象限角.则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.已知-<α<0,sin α+cos α=,则的值为( )
A. B. C. D.-
8.将函数f(x)=sin(2x+)的图象分别向左、向右平移φ(φ>0)个单位长度后,所得的图象都关于y轴对称,则φ的最小值分别为( )
A., B., C., D.,
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有错选的得0分.
9.下列命题正确的是( )
A.在与530°角终边相同的角中,最小的正角为170°
B.若角α的终边过点P(-4,3),则cos α=-
C.已知θ是第二象限角,则tan (sin θ)>tan (cos θ)
D.若一扇形弧长为2,圆心角为90°,则该扇形的面积为
10.已知函数f(x)=tan x,则下列结论正确的是( )
A.2π是f(x)的一个周期 B.f(-)=f()
C.f(x)的值域为RD.f(x)的图象关于点(,0)对称
11.已知函数f(x)=-cos (4x-),则下列说法错误的是( )
A.f(x)的最小正周期为π
B.f(x)的图象关于直线x=对称
C.f(x)的单调递增区间为[-,+](k∈Z)
D.f(x)的图象关于点(,0)对称
12.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,已知时间t=0时,点A的坐标是(,),则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间可以是( )
A.[0,1] B.[1,7] C.[7,12] D.[1,12]
三、填空题:本题共4小题,每小题5分,共20分.
13.写出一个定义域为R,周期为π的偶函数f(x)=________.
14.已知f(x)=sin x+tan x+x-1,若f(a)=3,则f(-a)=________.
15.把函数y=sin (5x-)的图象向右平移个单位,再把所得函数图象上各点的横坐标缩短为原来的,所得的函数图象对应的解析式为______________________.
16.已知函数f(x)=2sin (ωx-)+1(x∈R)图象的一条对称轴方程为x=π,其中ω为常数,且ω∈(1,2),则函数f(x)的最小正周期为________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知tan α=3,求下列各式的值:
(1);
(2)2sin2α-3sinαcos α-1.
18.(12分)已知θ是第二象限角,5sin θcos θ=4tan (π+θ),求:
(1)tan θ;
(2).
19.(12分)已知函数f(x)=sin (2x-).
(1)用五点法,画出函数f(x)在一个周期上的图象;
(2)当x∈[-,]时,f(x)-a=0有解,求实数a的取值范围.
20.(12分)已知函数f(x)=A sin (ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.
(1)写出函数f(x)的解析式及x0的值;
(2)求函数f(x)在区间[-,]上的最小值与最大值.
21.(12分)已知函数f(x)=sin (2x+φ),φ∈(0,π),且f(x)的图象关于x=对称.
(1)求f(x)的解析式;
(2)将f(x)图象上的所有点向左平移m(m>0)个单位,得到y=g(x)的图象,若y=g(x)的图象关于点(,0)对称,求当m取最小值时,函数y=g(x)的单调递增区间.
22.(12分)若函数f(x)=A sin (ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.
(1)求函数y=f(x)的解析式;
(2)当x∈[-,]时,不等式|f(x)-m|≤1有解,求实数m的取值范围.
第七章 素养测评
1.答案:B
解析:因为点P(,-)是角α的终边与单位圆的交点,所以cosα=,
故选B.
2.答案:A
解析:由sinα=-,且α是第三象限角,易得cosα=-,故tanα=.
3.答案:B
解析:弧长l=3r-2r=r,则圆心角α==1.
4.答案:B
解析:===|sinθcosθ|,由于θ为第二象限角,所以|sinθcosθ|=-sinθcosθ,故选B.
5.答案:B
解析:tan=tan (2π-)=tan (-)=-tan=-.故选B.
6.答案:C
解析:由题意得tan (α+2021π)=tanα<0,cos (α-)=sinα>0,由p能推出q,由q能推出p,故p是q的充要条件.故选C.
7.答案:B
解析:因为-<α<0,所以sinα<0,cosα>0,
又?sinα+cosα=
sin2α+cos2α=1?,即2cos2α-cosα-=0,解得cosα=,sinα=-,所以==,故选B.
8.答案:A
解析:函数f(x)的图象向左平移φ个单位长度得到函数g(x)=sin(2x+2φ+)的图象,向右平移φ个单位长度得函数h(x)=sin (2x-2φ+)的图象,于是,2φ+=+kπ,k∈Z,-2φ+=+kπ,k∈Z,于是φ的最小值分别为,.故选A.
9.答案:ABC
解析:选项A:由0°
选项B:由三角函数的定义可得cosα==-.正确;
选项C:∵θ是第二象限角,∴0
选项D:弧长为2,圆心角为90°,则扇形的半径为,所以扇形面积为×2×=.错误.故选ABC.
10.答案:ACD
解析:f(x)=tanx的最小正周期为π,所以2π是f(x)的一个周期,A项正确;f(-)=1,f()=-1,B项错误;f(x)=tanx的值域为R,C项正确;f(x)=tanx的图象关于点(,0)对称,D项正确.故选ACD.
11.答案:ABC
解析:对于函数f(x)=-cos (4x-),它的最小正周期为=,故A错误;当x=时,f(x)=0,故f(x)的图象关于点(,0)对称,故D正确,而B错误;令2kπ≤4x-≤2kπ+π,k∈Z,得+≤x≤+,k∈Z,故函数的增区间为[+,+],k∈Z,故C错误.故选ABC.
12.答案:AC
解析:由题意知T=12,∴ω==,从而设y关于t的函数为y=sin (t+φ).又∵t=0时,y=,∴可取φ=,∴y=sin (t+),∴当2kπ-≤t+≤2kπ+(k∈Z),即12k-5≤t≤12k+1(k∈Z)时,函数递增.∵0≤t≤12,∴函数的单调递增区间为[0,1]和[7,12].
13.答案:cos2x(答案不唯一)
解析:y=cos2x满足定义域为R,最小正周期T==π,且为偶函数,符合要求.
14.答案:-5
解析:由于f(a)=3,即sina+tana+a-1=3,故sina+tana+a=4,令g(x)=sinx+tanx+x,则g(-x)=-sinx-tanx-x=-g(x),即g(x)在定义域内是奇函数,满足sina+tana+a=-(sin (-a)+tan (-a)+(-a),则sin (-a)+tan (-a)+(-a)=-4,故f(-a)=sin (-a)+tan (-a)+(-a)-1=-4-1=-5.
15.答案:y=sin (10x-)
解析:将函数y=sin (5x-)的图象向右平移个单位,得到函数y=sin [5(x-)-]=sin (5x-)的图象,再把所得图象上各点的横坐标缩短为原来的,可得到函数y=sin (10x-)的图象.
16.答案:
解析:由f(x)=2sin (ωx-)+1(x∈R)图象的一条对称轴为直线x=π,可得ωπ-=kπ+(k∈Z),∴ω=k+(k∈Z).又∵ω∈(1,2),∴ω=,∴f(x)的最小正周期为T==.
17.解析:(1)原式====.
(2)原式=
===-.
18.解析:(1)由题意,角θ是第二象限角,且5sinθcosθ=4tan (π+θ),
可得5sinθcosθ=4tanθ=,可得cos2θ=,所以sin2θ=1-cos2θ=,
所以tan2θ==,
因为θ是第二象限角,可得tanθ=-.
(2)由(1)知tanθ=-,
又由====-.
19.解析:(1)列表如下:
x
2x- 0 π 2π
f(x) 0 0 - 0
描点、连线,如图所示.
(2)∵-≤x≤,
∴-≤2x-≤0,
∴-1≤sin (2x-)≤,
∴-≤sin (2x-)≤1.
∵f(x)-a=0有解,即a=f(x)有解,∴a∈[-,1].
20.解析:(1)∵A>0,ω>0,
∴由函数图象可知A=2,T==2[x0-(x0-)]=π,解得ω=2.
又∵函数图象过点(,2),∴2=2sin (2×+φ),
∴2×+φ=2kπ+(k∈Z),即φ=2kπ-,k∈Z.
又∵|φ|<,∴φ=,∴f(x)=2sin (2x+).
由函数图象可得2sin (2x0+)=,
∴2x0+=2kπ+,k∈Z,即x0=kπ-,k∈Z.
又∵-
当2x+=,即x=时,f(x)max=f()=2.
21.解析:(1)依题意有2×+φ=+kπ,k∈Z,
∴φ=+kπ,k∈Z,
又φ∈(0,π),∴φ=,
∴f(x)=sin (2x+).
(2)将f(x)图象上所有的点向左平移m(m>0)个单位,
得到y=g(x)=sin (2x++2m).
∵y=g(x)的图象关于点(,0)对称,
∴sin (2×++2m)=0,
∴+2m=kπ,k∈Z,
∴m=-,k∈Z.
∵m>0,∴当k=1时,m有最小值,
∴g(x)=sin (2x+).
由-+2kπ≤2x+≤+2kπ,k∈Z,
得[-+kπ,-+kπ],k∈Z.
∴函数的单调递增区间是[-+kπ,-+kπ],k∈Z.
22.解析:(1)由题图,知A=2,T=-(-)=,解得T=π,所以ω==2.根据“五点法”作图,可得2×+φ=2kπ+,k∈Z,解得φ=2kπ+,k∈Z.又因为|φ|<,所以φ=.所以f(x)=2sin (2x+).
(2)当x∈[-,]时,2x+∈[,],所以f(x)∈[1,2].
因为|f(x)-m|≤1有解,所以m-1≤f(x)≤1+m有解,即即
解得0≤m≤3.故实数m的取值范围是[0,3].
